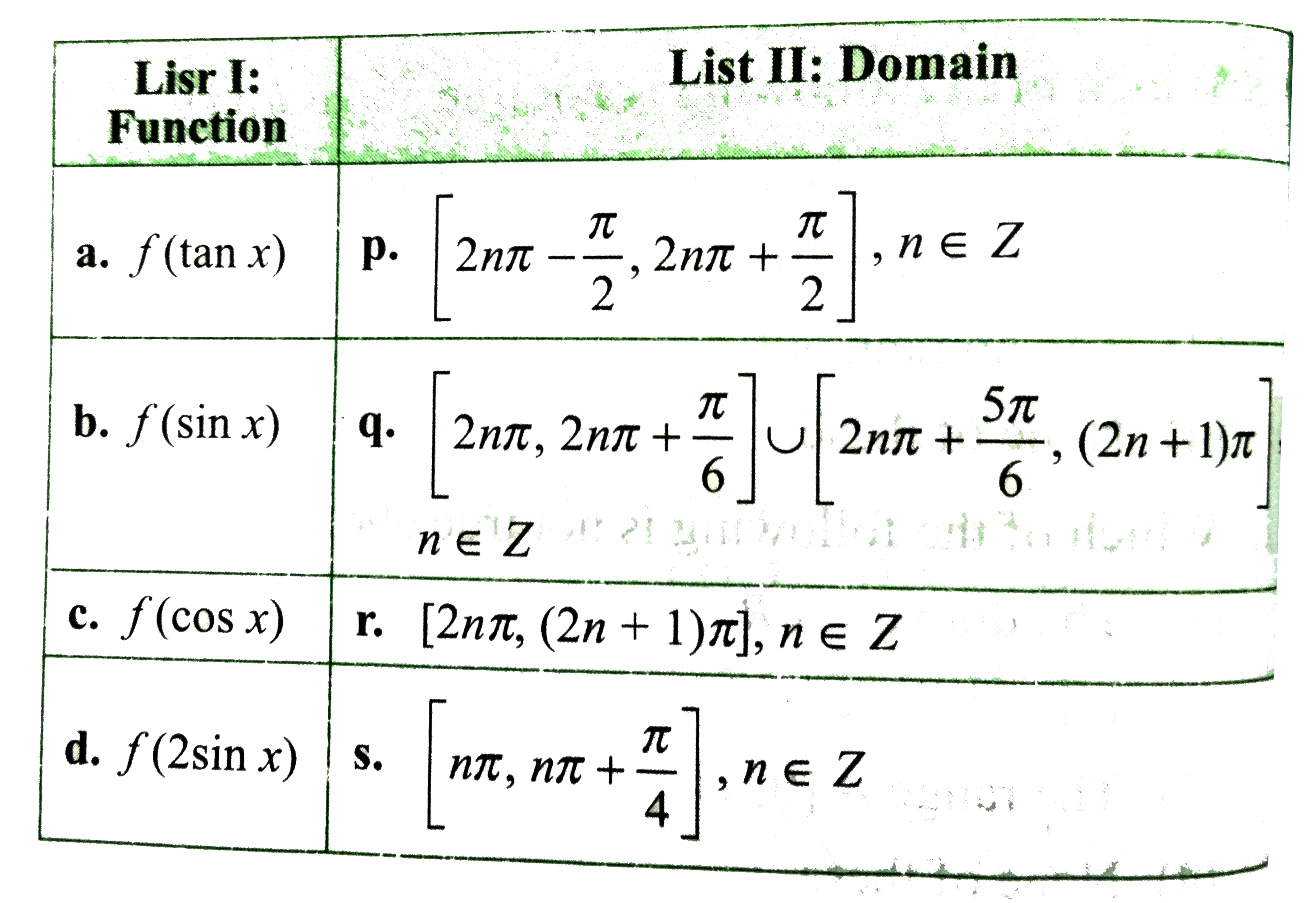Home
Class 12
MATHS
The function f(x) is defined on the inte...

The function `f(x)` is defined on the interval [0, 1]. Now, match the following lists:

Text Solution

Verified by Experts

The correct Answer is:
`a to s; b to r; c to p; d to q`
`f(tanx) " is defined if " 0 le tan x le 1`
`or x in [n pi, npi +(pi)/(4)], n in Z`
`f(sinx) " if defined if " 0 le sinx le 1`
`or x in [2n pi, (2n+1) pi], n in Z`
`f(cosx)" is defined if " 0 le cosx le 1`
`or x in [2n pi-(pi)/(2),2n pi+(pi)/(2)], n in Z`
`f(2sinx) " is defined if " 0 le 2sinx le 1 or 0 le sinx le 1//2`
`or [2n pi, 2n pi + (pi)/(6)] cup [2npi+(5pi)/(6),(2n+1)pi], n in Z`
Promotional Banner

Topper's Solved these Questions

  • RELATIONS AND FUNCTIONS

    CENGAGE ENGLISH|Exercise Numerical value Type|31 Videos

  • RELATIONS AND FUNCTIONS

    CENGAGE ENGLISH|Exercise Archives(single correct Answer Type)|9 Videos

  • RELATIONS AND FUNCTIONS

    CENGAGE ENGLISH|Exercise Linked Comprehension Type|32 Videos

  • PROPERTIES AND SOLUTIONS OF TRIANGLE

    CENGAGE ENGLISH|Exercise Archives (Numerical Value Type)|3 Videos

  • SCALER TRIPLE PRODUCTS

    CENGAGE ENGLISH|Exercise DPP 2.3|11 Videos

Similar Questions

Explore conceptually related problems

The function f(x)=x^(1//x) is increasing in the interval

{ . } denotes the fractional part function and [.] denotes the greatest integer function. Now, match the following lists:

The function f(x) is defined in [0,1] . Find the domain of f(tanx).

A function f is defined by f(x)=e^(x) sin x in [0,pi] . Which of the following is not correct?

If a funciton f(x) is defined for x in [0,1] , then the function f(2x+3) is defined for

The function f(x) = tan ^(-1)x -x decreases in the interval

Let the function f(x)=3x^(2)-4x+8log(1+|x|) be defined on the interval [0,1]. The even extension of f(x) to the interval [0,1]. The even extension of f(x) to the interval [-1,1] is

Let the function f(x)=x^(2)+x+sinx- cosx+log(1+|x|) be defined on the interval [0,1]. The odd extension of f(x) to the interval [-1,1] is

Let f:[0,1] rarr R be a function.such that f(0)=f(1)=0 and f''(x)+f(x) ge e^x for all x in [0,1] .If the fucntion f(x)e^(-x) assumes its minimum in the interval [0,1] at x=1/4 which of the following is true ?

The function f(x) = x^(x) , x gt 0 , is increasing on the interval

Knowledge Check

  • The function f(x) = x^(x) , x gt 0 , is increasing on the interval

    A
    (0, e]
    B
    `(0, (1)/(e))`
    C
    `[(1)/(e),infty)`
    D
    none of these