Text Solution
Verified by Experts
Topper's Solved these Questions
Similar Questions
Explore conceptually related problems
SUNSTAR PUBLICATION-II PUC CHEMISTRY SUPPLEMENTARY EXAM QUESTION PAPER JUNE -2019-PART-D
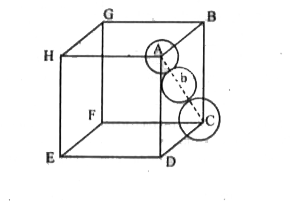
- Calculate the packing efficiency in Face Centred Cubic (FCC) structure...
Text Solution
|
- Give any two differences between Frenkel and Schottky defects .
Text Solution
|
- On dissolving 2.34g of non-electrolyte solute in 40g of benzene, the b...
Text Solution
|
- State Henry's law.
Text Solution
|
- How solubility of a gas in liquid changes with increase in temperature...
Text Solution
|
- For a given data : E(Mg^(2+) // Mg)^(@) = -2.37 V , E(Cu^(2+)// Cu)^(@...
Text Solution
|
- State Kohlrausch law of independent migration of ions.
Text Solution
|
- Write the overall cell reaction in mercury cell.
Text Solution
|
- Derive an integrated rate equation for the rate constant of a first-or...
Text Solution
|
- The rate constant of a reaction is doubled when the temperature increa...
Text Solution
|
- How is Gold-sol prepared by Bredig's-arc method?
Text Solution
|
- What is homogenous catalysis? Give an example.
Text Solution
|
- How does entropy change for adsorption?
Text Solution
|
- (a) Write the equations for the steps involved in SN^(1) mechanism for...
Text Solution
|
- Explain Friedel -Crafts alkylation for chlorobenzene. Give equation.
Text Solution
|
- What is racemic mixture ?
Text Solution
|
- Write the mechanism of acid catalysed dehydration of ethanol to ethene...
Text Solution
|
- Write general equation for preparation of ether by Williamson synthesi...
Text Solution
|
- Among alcohols and phenols which one is more acidic?
Text Solution
|
- Comlete the following chemical reaction RCH2OH underset(2.H(3)O^(+))o...
Text Solution
|