Basic Geometrical Ideas

1.0Basic Terms

Point

A point is an exact location in space. It has no length and no width. We represent a point by a dot (.) and label it with a capital letter. Some representations of a point in everyday life are shown below.

Line

A line is a straight path of points that extends on and on in both the directions without ever ending. It has one dimension. The length of a line cannot be measured. To show that a line extends endlessly in both the directions, we use arrowheads at both the ends. A line is named by using any two points on it. Thus, the line given alongside is named as line $AB$ or line $BA$ and represented as $\overleftrightarrow{\mathrm{AB}}$ or $\overleftrightarrow{\mathrm{BA}}$. Through and two points, there is exactly one line.

A horizontal line goes straight across.

A vertical line goes straight up and down.

A line can also be curved. A curved line is called a curve.

Plane

A plane is a flat surface. A plane has two dimensions. It is represented by a shape that looks like a floor or a wall, but it extends without end. In mathematics, a plane goes on and on in all directions without end. We usually work with just a part of a plane. Points and lines lie on a plane.

Through any three points not on the same line, there is exactly one plane. You can use three points that are not all on the same line to name a plane. The given figure shows plane ABC. The order of the points does not matter. Some representations of a plane surface from our everyday life are:

Collinear points are points that lie on the same line. Coplanar points are points that lie in the same plane.

Line Segment and ray (defined terms)

In geometry, terms that can be described using known words such as point or line are called defined terms.

Line Segment

The line segment $AB$ or segment $AB$, (written as $\overline{AB}$ ) consists of the endpoints $A$ and $B$ and all points on $\overline{\mathrm{AB}}$ that are between A and B . Note that $\overline{\mathrm{AB}}$ can also be named $\overline{\mathrm{BA}}$.

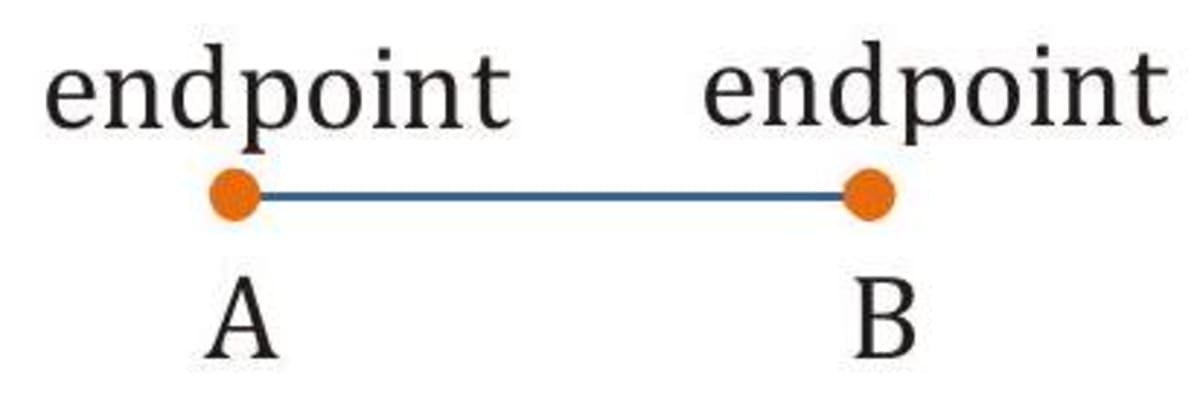
Ray

The ray $AB$ (written as $\overrightarrow{AB}$ ) consists of the endpoint $A$ and all points on $\overrightarrow{\mathrm{AB}}$ that lie on the same side of A as B . Note that $\overrightarrow{\mathrm{AB}}$ and $\overrightarrow{\mathrm{BA}}$ are different rays.

If point $C$ lies on $\overrightarrow{AB}$ between $A$ and $B$, then $\overrightarrow{CA}$ and $\overrightarrow{CB}$ are opposite rays.

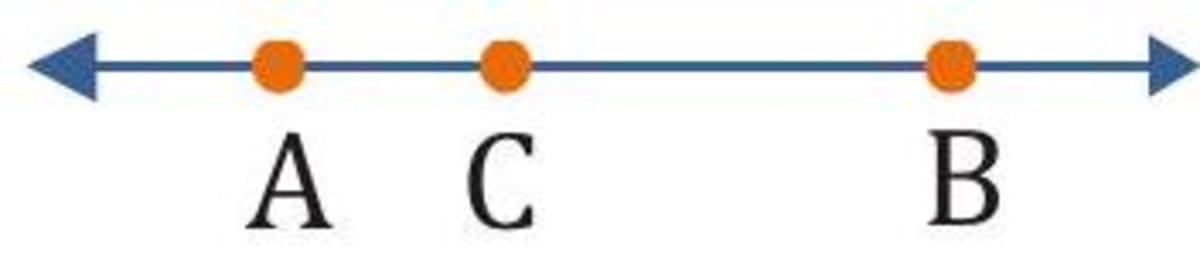
Segments and rays are collinear if they lie on the same line. So, opposite rays are collinear. Lines, segments, and rays are coplanar if they lie in the same plane.

Intersecting lines

When two or more lines intersect at a common point they are known as intersecting lines. The point at which they cross each other is known as point of intersection.

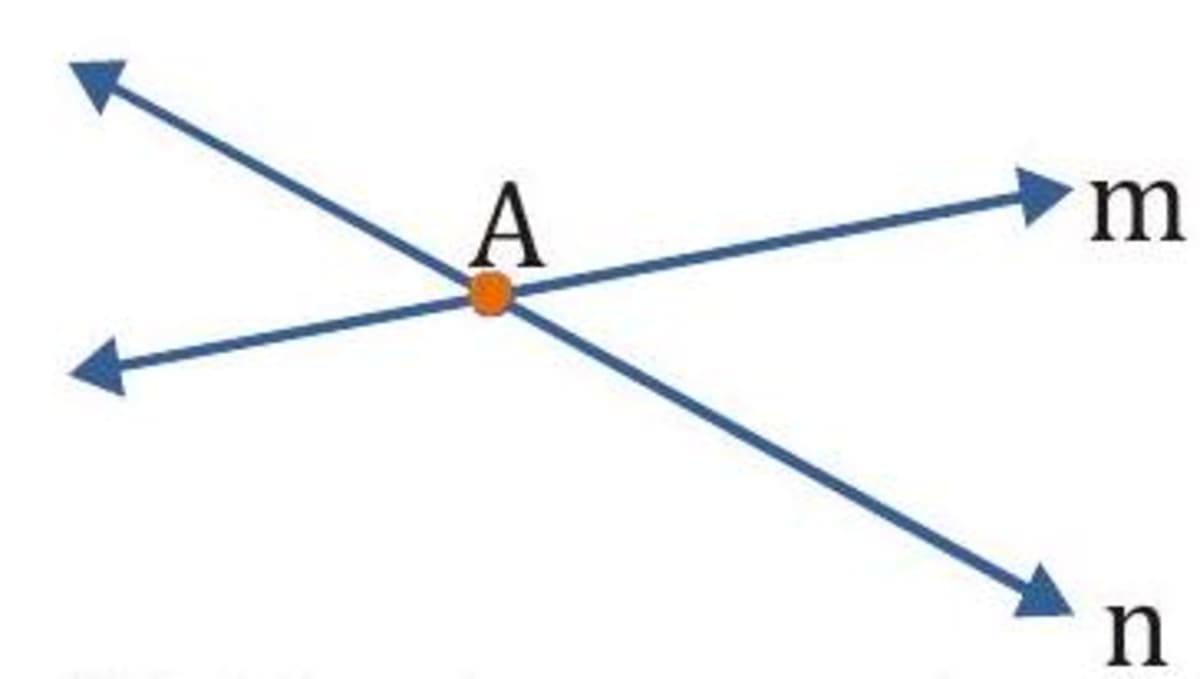
Note: There are unlimited number of lines through a point. Three or more lines in a plane are said to be concurrent if all of them pass through the same point and this point is called point of concurrence of the given lines.

Parallel lines

Two lines in the same plane either meet or do not meet. Lines that do not meet are parallel lines. $AB$ and $CD$ are horizontal parallel lines. PQ and RS are vertical parallel lines.

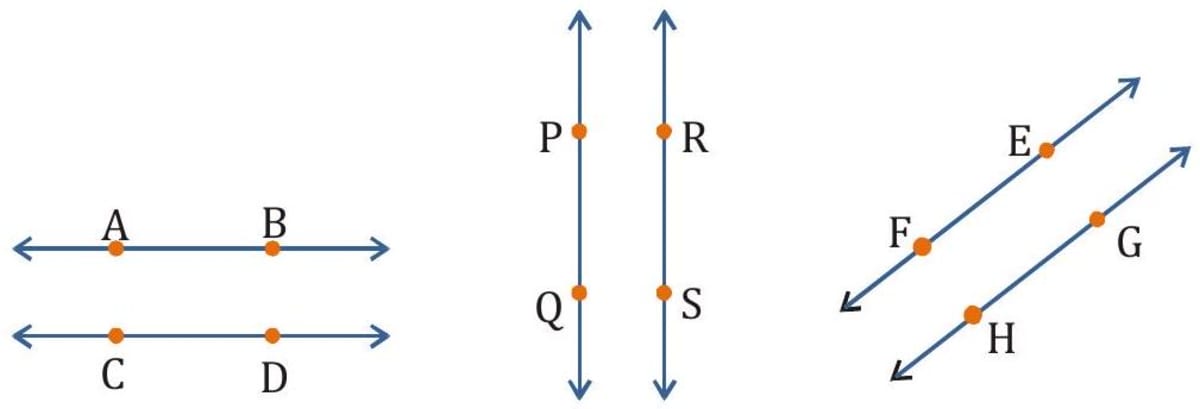
• The perpendicular distance between two parallel lines remains the same throughout.
• The rails of a railway line, opposite edges of a ruler and the opposite sides of a rectangle are examples of parallel lines.
• If two lines are not parallel, then they are intersecting.
  

2.0Plane figure, Interior and Exterior Figure

In geometry, any collection of points is called a figure. If all the points in a figure are in one plane, the figure is a plane figure.

So we can say that a line segment is plane figure.

Open and closed figures

Open figures do not begin and end at the same points.

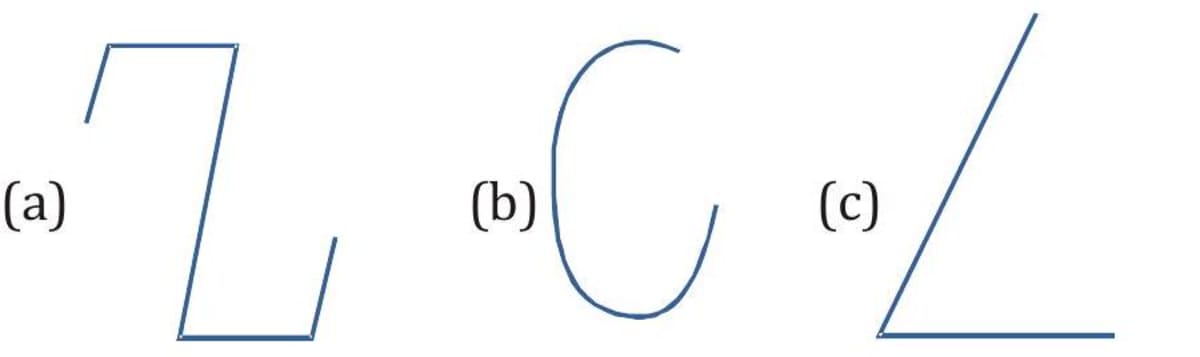
Closed figures begin and end at the same points.

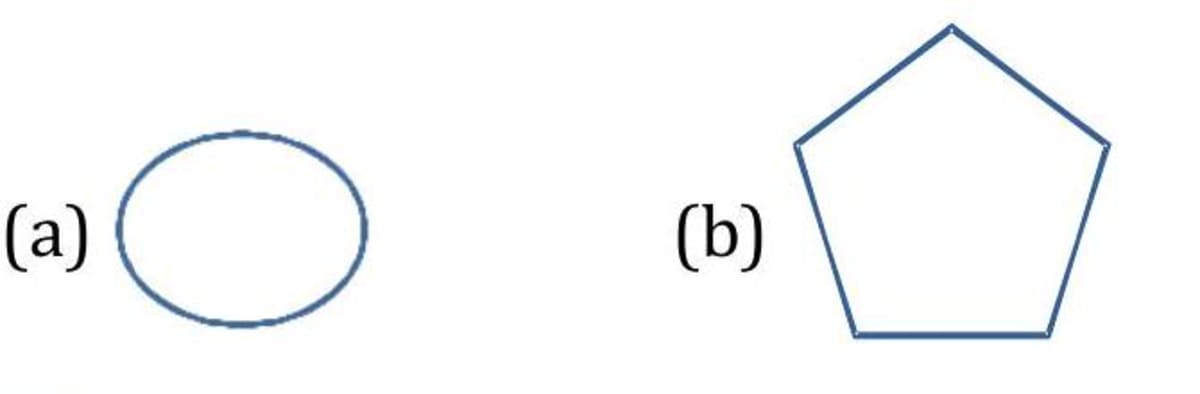
Interior and exterior of a figure

Your house has a boundary wall. The boundary wall separate your house from the main road and adjoining houses. There can be three cases - you are inside your house, you are just at the gate of the house or you are on the road, i.e. outside the house. Similarly, if we have a closed figure, there are three cases :

3.0Polygons

A simple closed figure formed of three or more line segments is called a polygon.

• Triangle is the smallest polygon with minimum sides.

Sides

The line segments forming a polygon are called its sides. $ABCD$ is a polygon in which $AB$, $BC,CD$ and $DA$ are its four sides.

Vertices

The meeting point of a pair of sides of a polygon is called its vertex. Thus, A, B, C, D are the four vertices of given polygon ABCD.

Adjacent sides

Any two sides of a polygon having a common end point are called its adjacent sides. Thus ( $\mathrm{AB},\mathrm{BC}$ ), ( $\mathrm{BC},\mathrm{CD}$ ), ( $\mathrm{CD},\mathrm{DA}$ ) and ( $\mathrm{DA},\mathrm{AB}$ ) are four pairs of adjacent sides in the given polygon $ABCD$. Here (A, B), (B, C), (C, D) and (D, A) are the pairs of adjacent vertices. Diagonals : A line segment joining two non-adjacent vertices of a polygon is called its diagonal. Thus, AC and BD are the diagonals of the given polygon ABCD .

4.0Angles

An angle is made up of two rays that have the same end point. The end point at which the two rays meet is called the vertex of the angle. Each of the rays that form the angle are called the arms of the angle.

The sign of angle is represented by $\angle$. Here, angle is $\angle \mathrm{BAC}$.

The size of an angle depends on the rotation up to the terminal side. The amount of this rotation is called the measure of the angle.

The ray which represents the starting position is called the initial side of the angle and the ray which indicates the stopping position is called the terminal side of the angle.

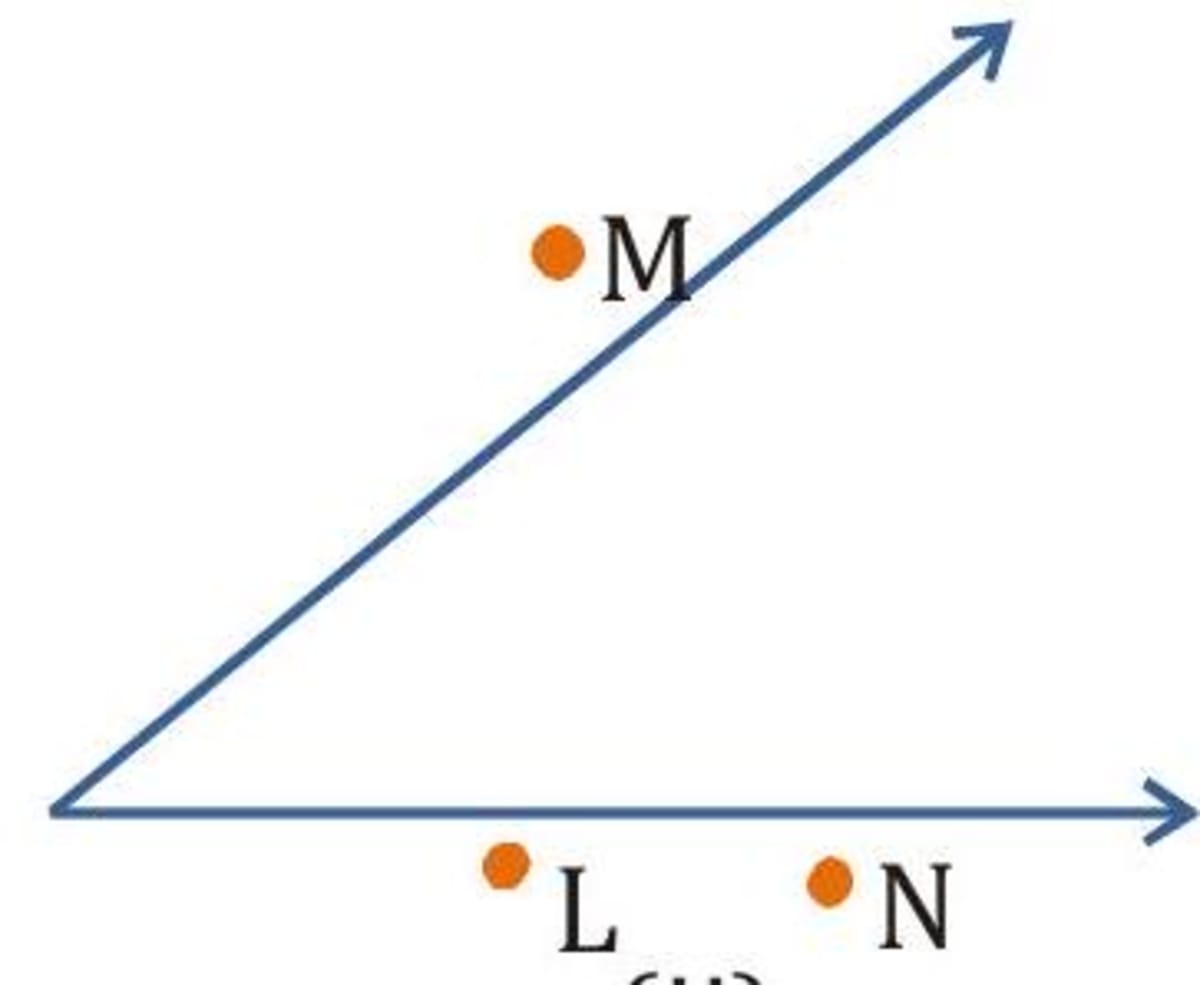
Interior and exterior of an angle

Like any plane figure, an angle divides the plane in which it lies into two parts. One part is called the inside region or the interior of an angle. The other part is called the outside region or the exterior of an angle.

The points $\mathrm{P},\mathrm{Q},\mathrm{R},\mathrm{S}$ lie in the interior of an angle. The points $\mathrm{L},\mathrm{M},\mathrm{N}$ lie in the exterior of an angle.

Name the angles $\angle 1,\angle 2,\angle 3$ and $\angle 1+\angle 2$ in the following figure.

• Explanation $\angle 1=\angle \mathrm{NCB}$ $\angle 2=\angle \mathrm{MCN}$ $\angle 3=\angle \mathrm{DCM}$ $\angle 1+\angle 2=\angle \mathrm{MCB}$ Note: A quarter turn of a ray $\overrightarrow{\mathrm{OA}}$ about " O " describe an angle called a right angle. The measure of right angle is $90^{\circ }$.

5.0Triangle

A triangle is a simple closed figure made of three-line segments. Triangle $ABC$ is denoted by the symbol $△ABC$.

Median of a triangle

A line segment joining a vertex to the midpoint of the side opposite to the vertex is called a median of a triangle. Here in $△ABC,D,E,F$ are the mid points of the sides $BC,AC$ and $AB$ respectively. The medians are $\mathrm{AD},\mathrm{BE}$ and CF . The point of intersection of three medians is called centroid (G).

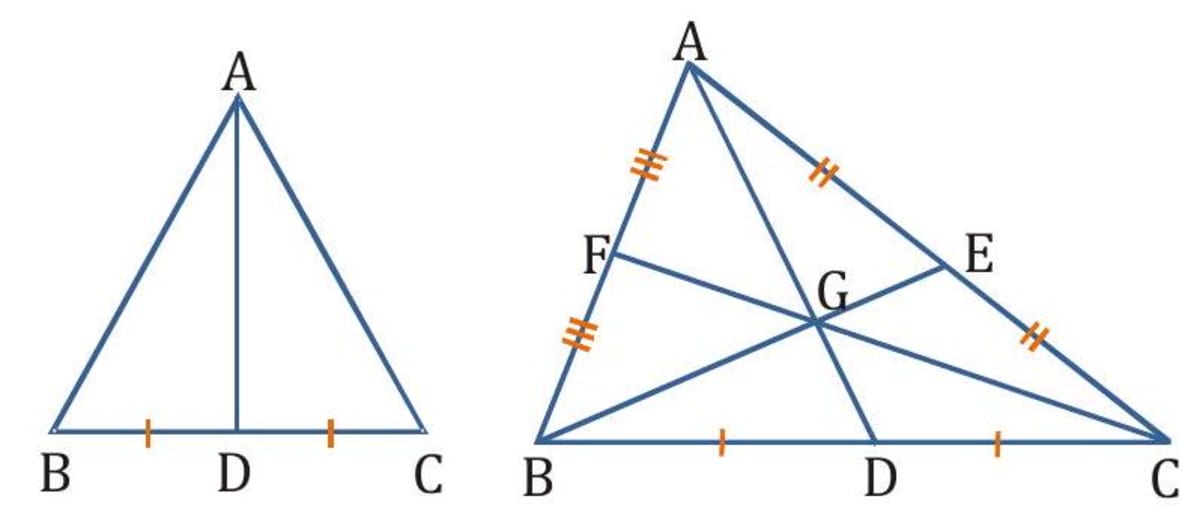
Altitude of a triangle

An altitude of a triangle is the perpendicular drawn from a vertex to the opposite side. If we take BC as the base, then AD is called the height of the triangle. Every triangle has three altitudes, one from each vertex. The point of intersection of altitude is called orthocentre.

Note: Two triangle are said to be congruent if every angle of one is equal to the corresponding angle of the other and every side of one is equal to the corresponding side of the other.

6.0Quadrilaterals

A quadrilateral is a four sided polygon. It has 4 sides and 4 angles.

7.0Circles

A circle is a simple closed curve all of whose points are at the same distance from a given point $O$ in the same plane. The given point 0 is called the centre of the circle.

Part of a circle

Radius : A line segment joining the centre of a circle to any point on the circle is called a radius of that circle.

Chord : A line segment joining any two points on a circle is called a chord of that circle.

Diameter : A chord that passes through the centre of a circle is called a diameter of that circle. The diameter is twice the radius.

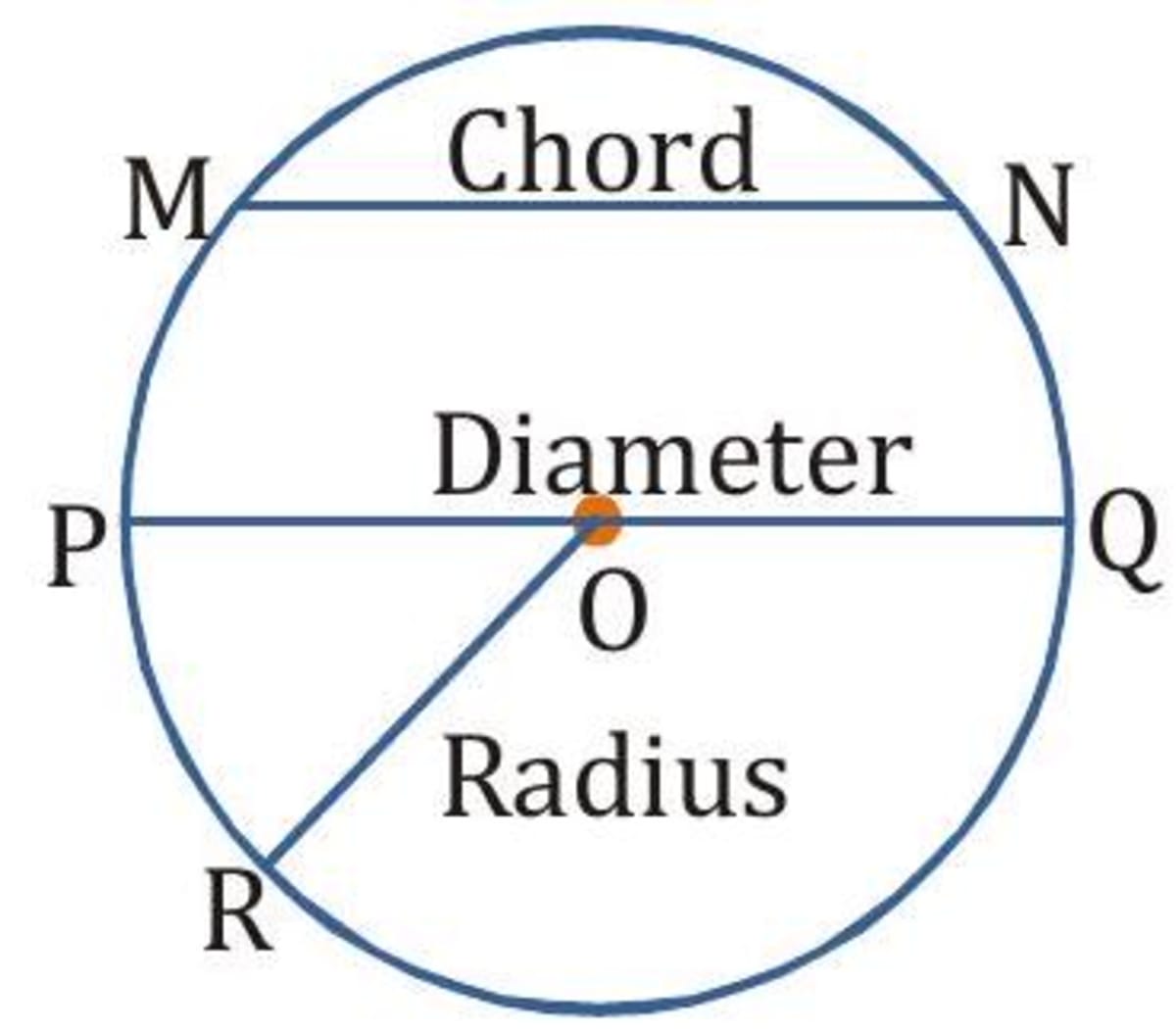
In figure, $\mathrm{MN},\mathrm{PQ}$ and OR are chord, diameter and radius respectively. All the diameters of a circle meet at the centre of the circle.

Circumference : The perimeter of a circle is called its circumference. In other words, the length of the boundary of the interior of a circle is its circumference.

Secant : A line which intersects or meets the circle at two distinct points is called a secant. $\overleftrightarrow{\mathrm{PQ}}$ is a secant.

Arc : A part (continuous) of a circle is called an arc. Semi circle : A diameter divides a circle into two equal parts which are called semi circles.

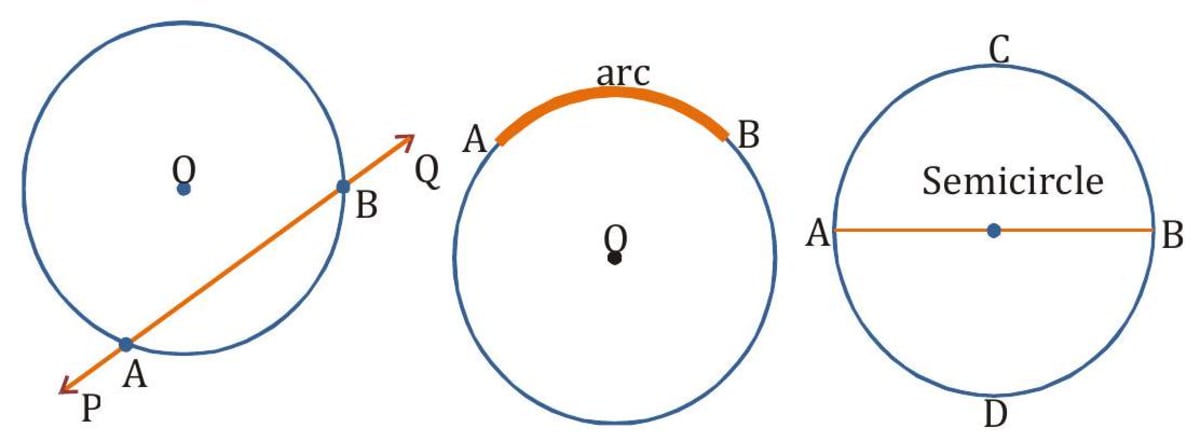
Segment : A chord AB of a circle divides the area enclosed by it into two parts which are called segments.

The smaller part is called a minor segment and the larger part is called a major segment.

Sector and quadrant : The part of a circle enclosed by any two radii of the circle is called a sector of the circle. In this figure, OACB is a sector.

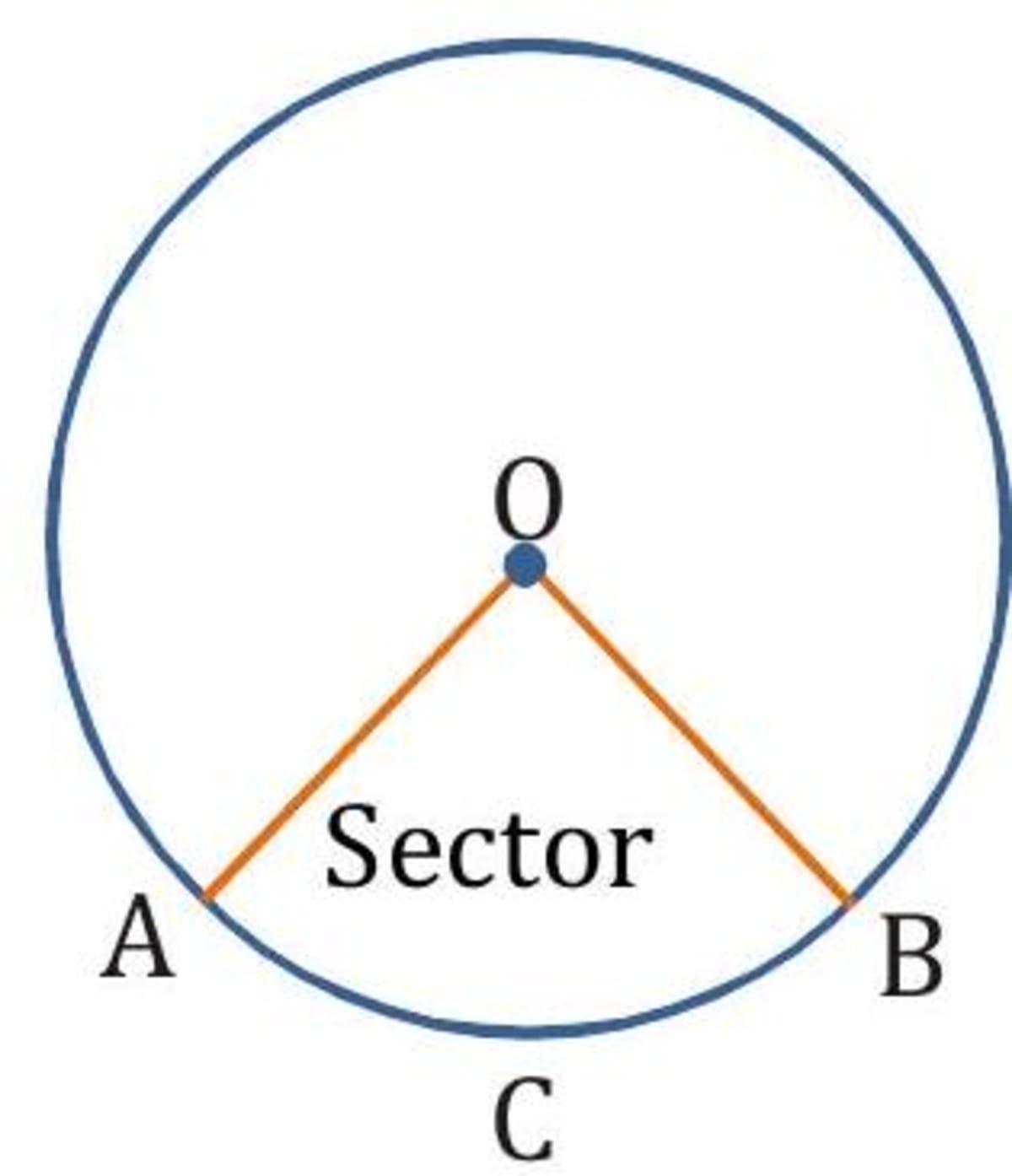
If two radii are at right angles to each other, the sector is called a quadrant. A quadrant is $1/4$ the of a circle.

8.0Building Concepts

Answer the following questions in real life examples of Point, Line and Plane. (i) A location of a place in the Map. (ii) The tip of a needle. (iii) Lines of latitude and longitude. (iv) The centre - line on a highway. (v) White - board.

• Explanation (i) Point (ii) Point (iii) Line (iv) Line (v) Plane

Draw and label each of the following. (i) $\overleftrightarrow{\mathbf{PQ}}$ (ii) Points S and T (iii) Plane EFGH

• Solution (i)
  
  (ii)
  
  (iii)
  

Give two other names for $\overleftrightarrow{\mathbf{PQ}}$ and for plane $R$.

• Explanation Other names for $\overleftrightarrow{\mathrm{PQ}}$ are $\overleftrightarrow{\mathrm{QP}}$ and line n. Other names for plane R are plane SVT and plane PTV.

Name three points that are collinear. Name four points that are coplanar.

• Explanation Points S, P and T lie on the same line, so they are collinear. Points S, P, T and V lie in the same plane, so they coplanar.
  

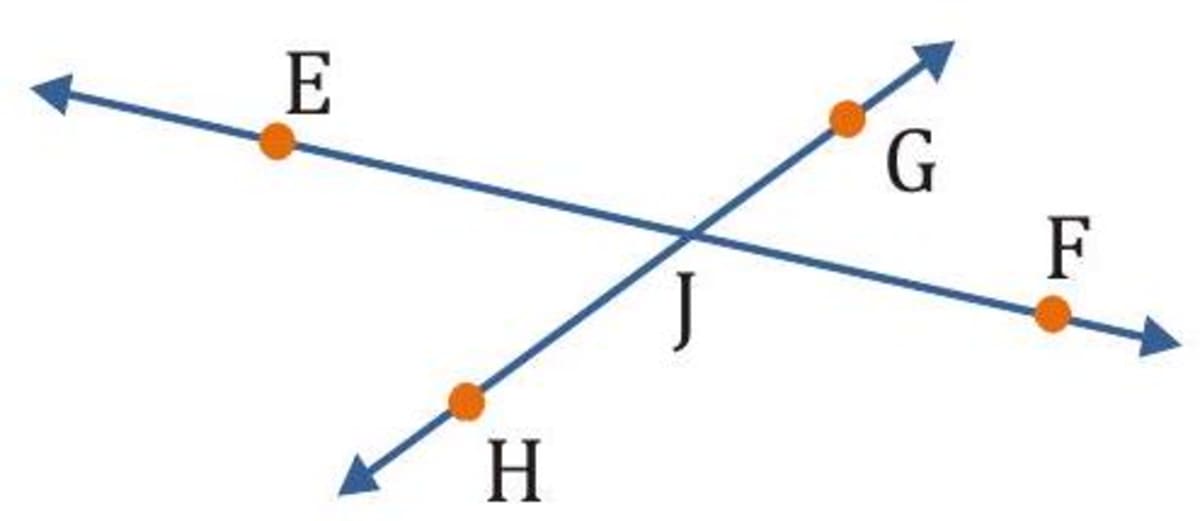
• Explanation (i) Another name for $\overline{\mathrm{GH}}$ is $\overline{\mathrm{HG}}$. (ii) The rays with endpoint J are $\overrightarrow{\mathrm{JE}},\overrightarrow{\mathrm{JG}},\overrightarrow{\mathrm{JF}}$ and $\overrightarrow{\mathrm{JH}}$. The pairs of opposite rays with endpoint J are $\overrightarrow{\mathrm{JE}}$ and $\overrightarrow{\mathrm{JF}},\overrightarrow{\mathrm{JG}}$ and $\overrightarrow{\mathrm{JH}}$.

Sketch a plane (i) and a line that is in the plane. (ii) and a line that does not intersect the plane. (iii) and a line that intersects the plane at a point.

• Explanation (i)
  
  (ii)
  
  (iii)
  

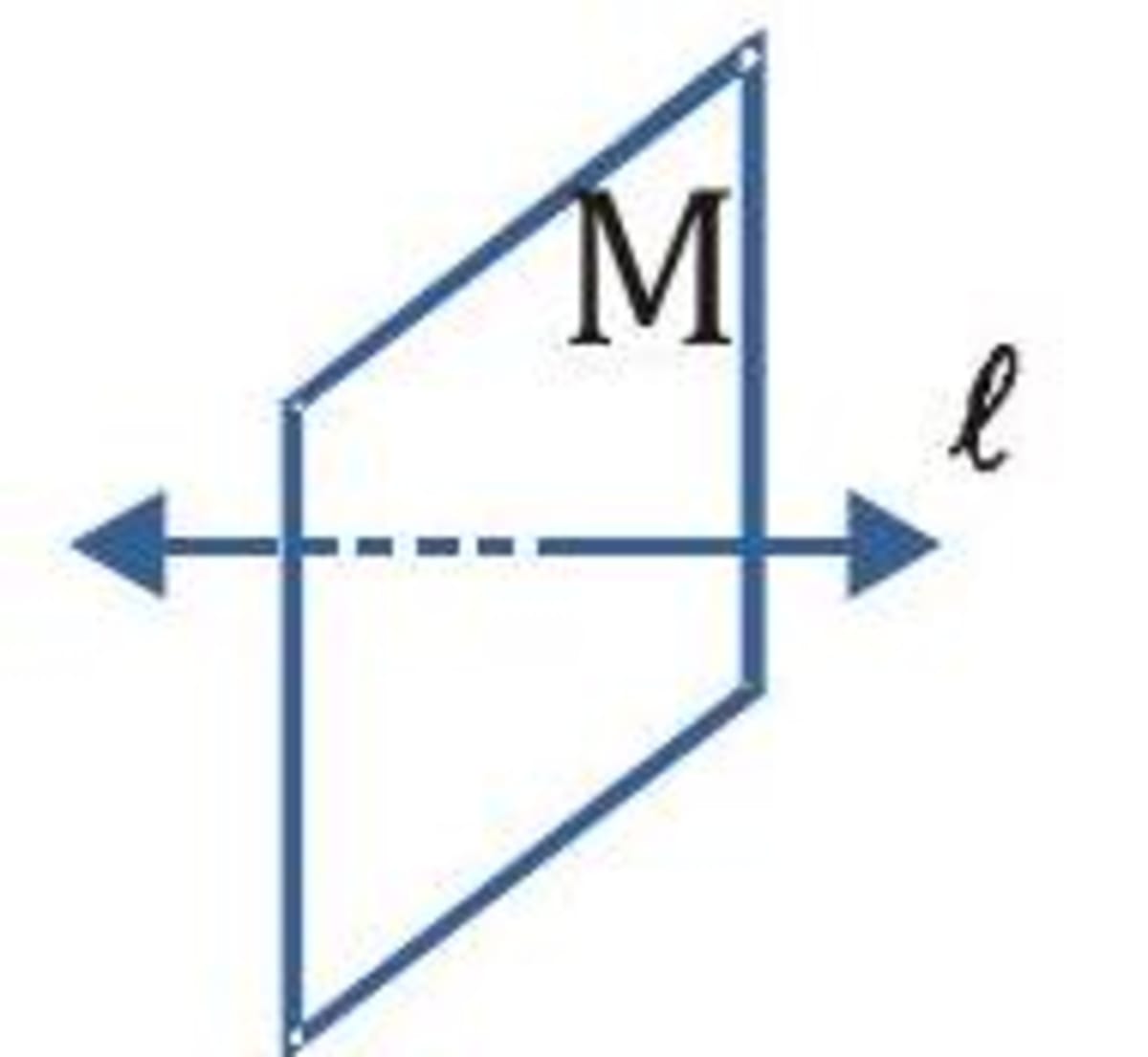
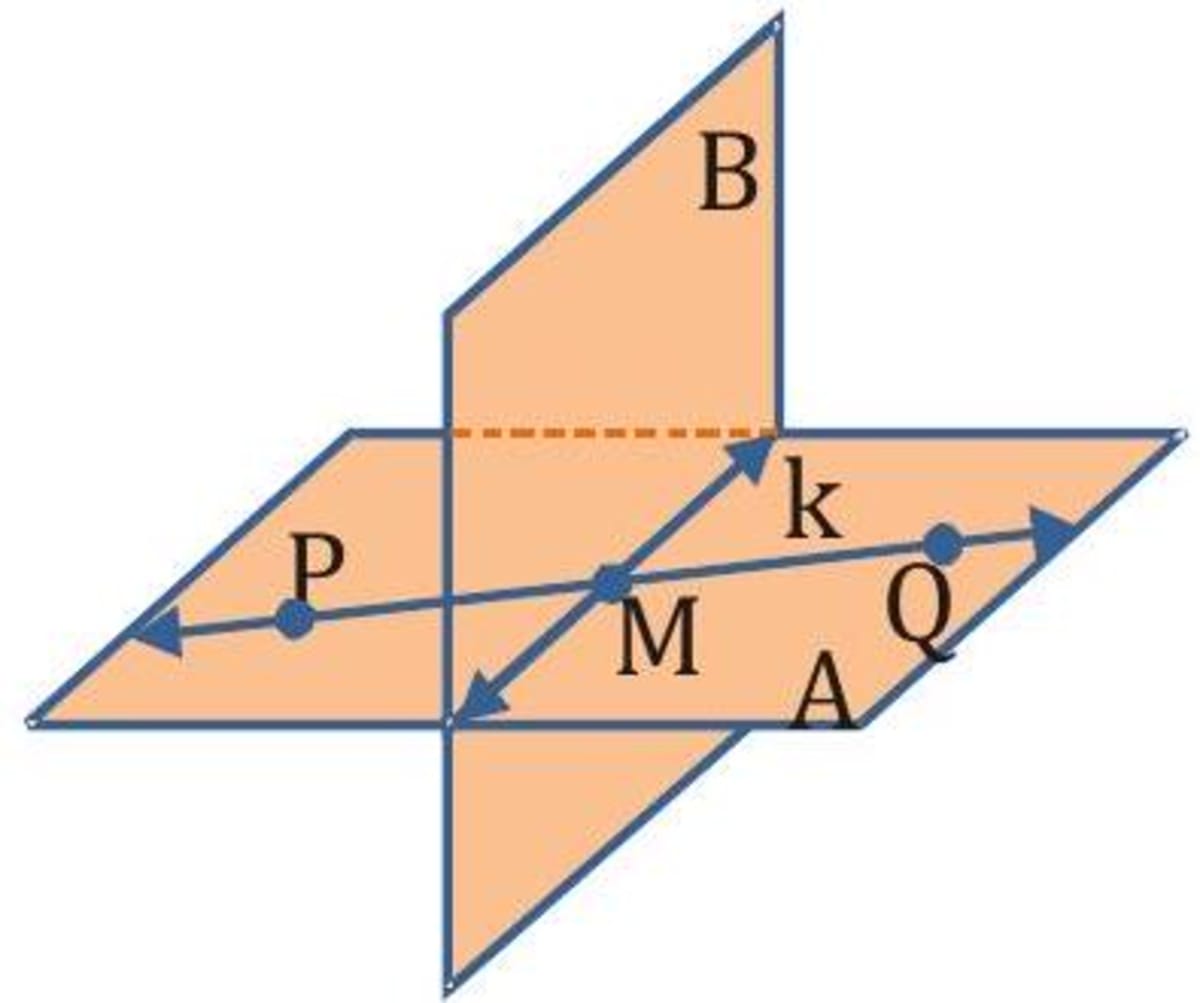
Sketch two planes that intersect in a line.

• Solution Step 1: Draw a vertical plane. Shade the plane. Step 2: Draw a second plane that is horizontal. Shade this plane with a different colour. Use dashed lines to show where one plane is hidden. Step 3: Draw the line of intersection.
  

In the given diagram, name the point (s)

• Explanation (i) A (ii) $\mathrm{C},\mathrm{A},\mathrm{D}$ (iii) B, E, O, F

Which of the following are simple closed figures and which are polygons?

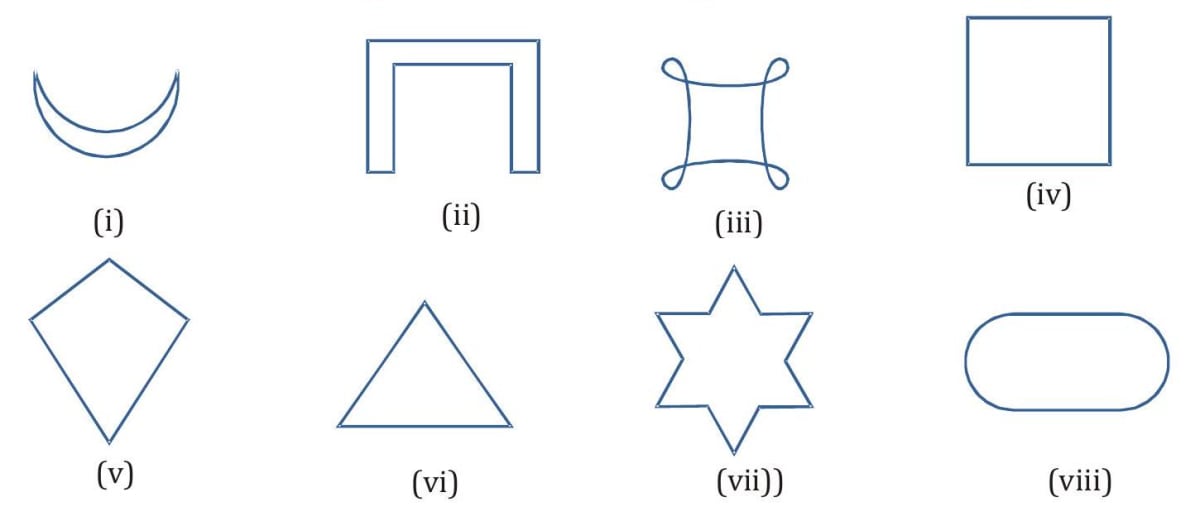
• Solution Figures (i), (ii), (iv), (v), (vi), (vii), (viii) are simple closed figures because they do not intersect itself. Figure (ii), (iv), (v), (vi), (vii) are polygons because they are made of three or more line segments.

(i) Identify all the triangles in figure. (ii) How many angles are there in the figure? Write their names. (iii) Write the names of six line segments. (iv) Which two triangles have $\angle \mathrm{B}$ as common in the figure? Name them.

• Solution (i) $△\mathrm{ABD},△\mathrm{ADC},△\mathrm{ABC}$ (ii) There are 8 angles in the figure $\angle \mathrm{ABD},\angle \mathrm{BAD},\angle \mathrm{ADB},\angle \mathrm{ADC},\angle \mathrm{DAC},\angle \mathrm{ACD},\angle \mathrm{BAC},\angle \mathrm{BDC}$ (iii) $\mathrm{AB},\mathrm{BD},\mathrm{DC},\mathrm{BC},\mathrm{AC},\mathrm{AD}$ (iv) $△\mathrm{ABD}$ and $△\mathrm{ABC}$ have $\angle \mathrm{B}$ as common.

Take a point 0 inside a given quadrilateral $ABCD$. Join the point 0 to the vertices $A$, $B,C$ and $D$. Into which figures the quadrilateral will be divided?

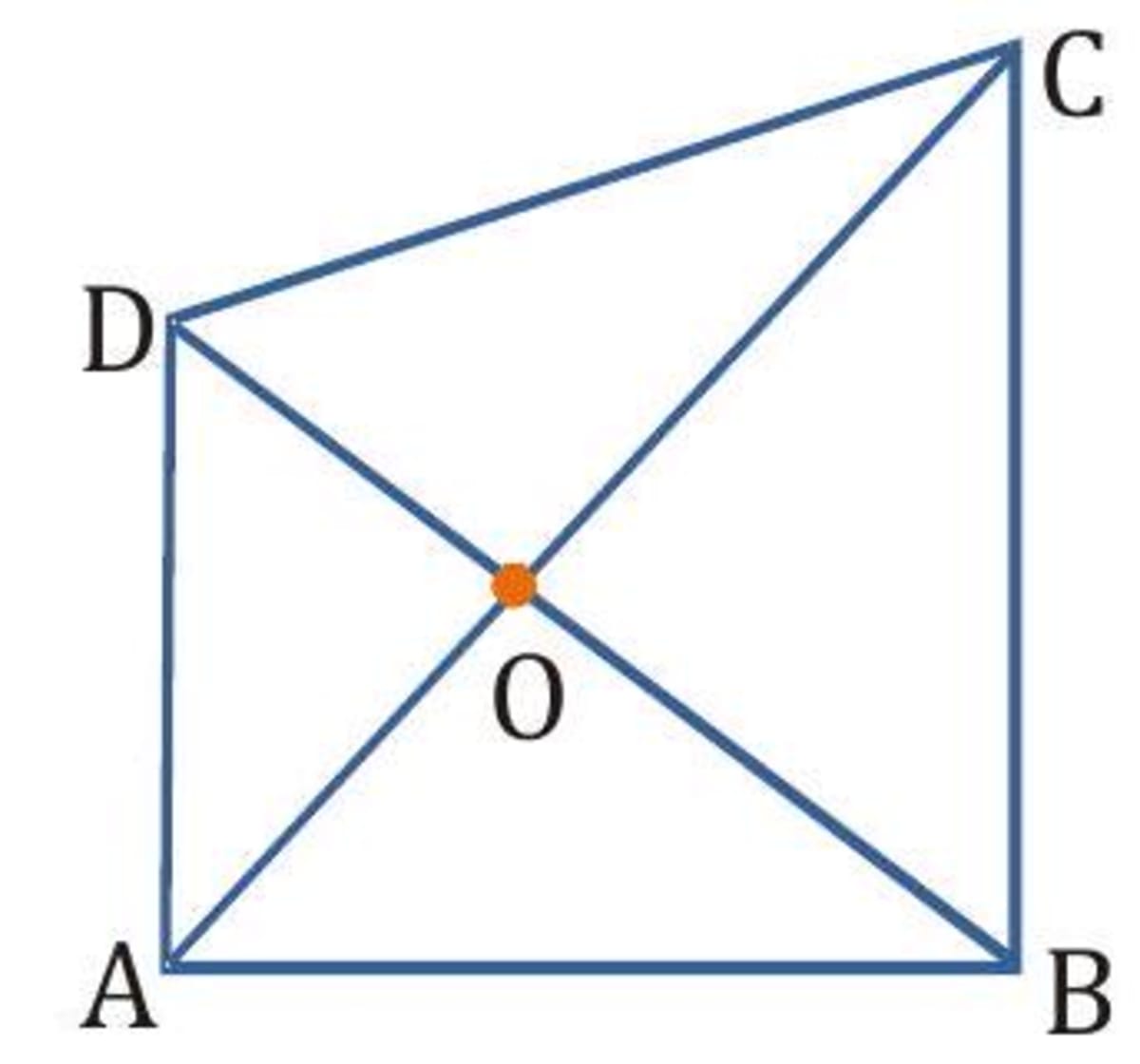
• Explanation The quadrilateral is divided into 4 triangles that are $△BOC,△COD,△DOA,△AOB$.

Study the given figure and answer the following.

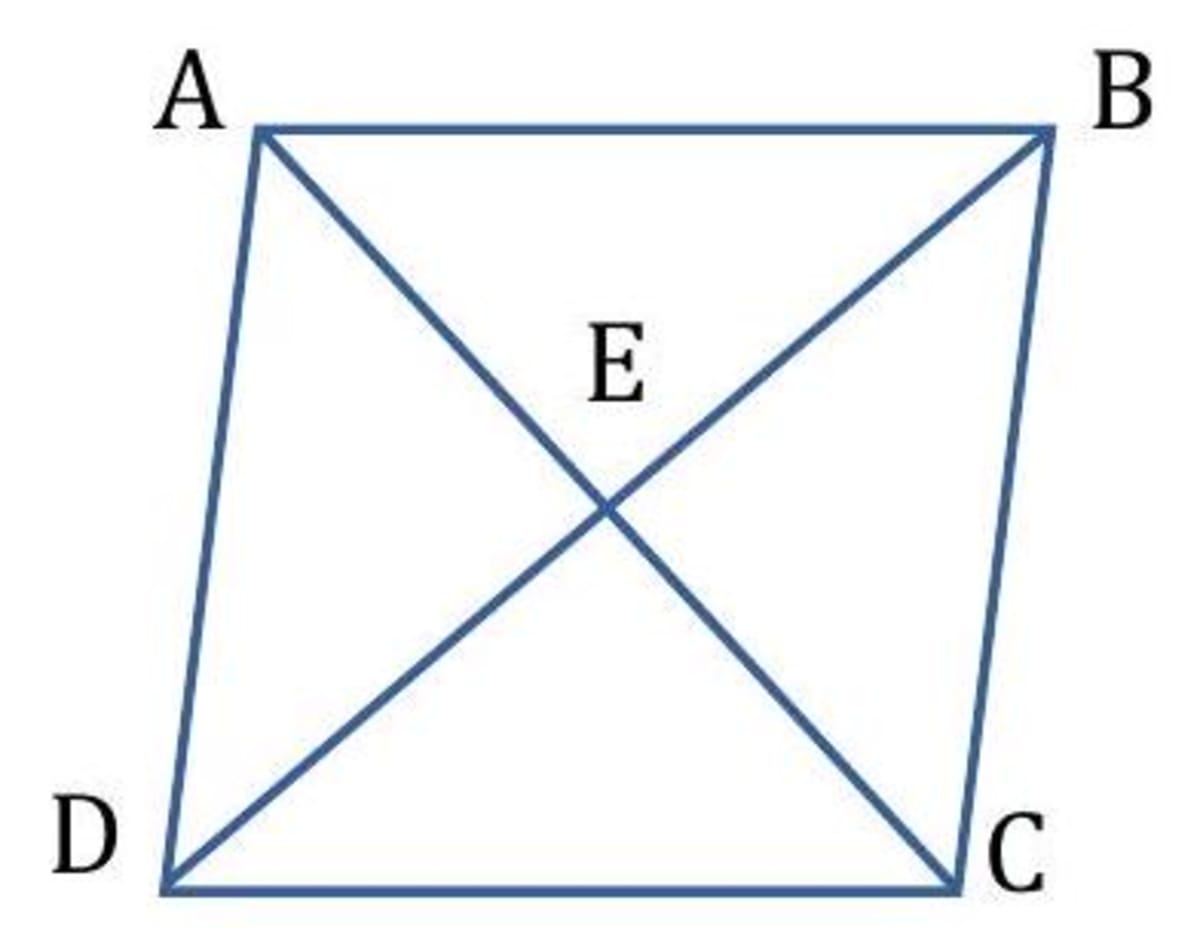
• Solution
  
  (i) $\angle \mathrm{EDC}$ can be named as $\angle \mathrm{CDE},\angle \mathrm{BDC}$ and $\angle \mathrm{CDB}$. (ii) E is the vertex of $\angle \mathrm{AEB}$ (iii) Three angles are formed at vertex D i.e. $\angle \mathrm{ADB},\angle \mathrm{BDC}$ and $\angle ADC$. (iv) Eight triangles i.e.; $△\mathrm{DEC},△\mathrm{AEB},△\mathrm{AED},△\mathrm{BEC},△\mathrm{ADC},△\mathrm{ABC}$,

Use circle to name following figures.

• Explanation (i) The three radii are $\mathrm{OA},\mathrm{OB}$ and OC . (ii) The three chords are $\mathrm{AC},\mathrm{BC}$ and AB . (iii) The diameter is AB . (iv) The triangle that has centre as a vertex are $△AOC$ and $△BOC$.

• Solution (i) COA, AOD, DOB, BOC four quadrants of the circle. (ii) PAQNP is a minor segment of the circle. (iii) PBQNP is a major segment of a circle.
  

9.0Memory Map