NEETClass 11thClass 12thClass 12th PlusJEEClass 11thClass 12thClass 12th PlusClass 6-10Class 6thClass 7thClass 8thClass 9thClass 10thOnline CoursesDistance LearningInternational OlympiadNEETClass 11thClass 12thClass 12th PlusJEE (Main+Advanced)Class 11thClass 12thClass 12th PlusJEE MainClass 11thClass 12thClass 12th PlusClass 6-10Class 6thClass 7thClass 8thClass 9thClass 10thNEET2025202420232022JEE20262025202420232022Class 6-10JEE MainPrevious Year PapersSample PapersMock TestResultAnalysisSyllabusExam DatePercentile PredictorAnswer KeyCounsellingEligibilityExam PatternJEE MathsJEE ChemistryJEE PhysicsJEE AdvancedPrevious Year PapersSample PapersMock TestResultAnalysisSyllabusExam DateAnswer KeyEligibilityExam PatternRank PredictorNEETPrevious Year PapersSample PapersMock TestResultAnalysisSyllabusExam DateCollege PredictorAnswer KeyRank PredictorCounsellingEligibilityExam PatternBiologyNCERT SolutionsClass 6Class 7Class 8Class 9Class 10Class 11Class 12TextbooksCBSEClass 12Class 11Class 10Class 9Class 8Class 7Class 6SubjectsSyllabusNotesSample PapersQuestion PapersICSEClass 10Class 9Class 8Class 7Class 6State BoardBiharKarnatakaMadhya PradeshMaharashtraTamilnaduWest BengalUttar PradeshOlympiadMathsScienceEnglishSocial ScienceNSOIMONMTCASATInstant Online ScholarshipAIOT(NEET)TALLENTEXALLEN for SchoolsAbout ALLENBlogsNewsCareersRequest a call backBook a demo
Visualising Solid Shapes
1.0Geometric Solids
(i) Geometric solids are three- dimensional figures that have length, breadth and height. (ii) Every geometric solid has a fixed number of edges, vertices and faces. (iii) The face of a solid is a flat or curved surface that is two-dimensional in shape. (iv) Every solid has flat surfaces or curved surfaces or both types of surfaces (flat and curved). (v) A solid with all its surfaces flat is a polyhedron. Each surface of a polyhedron is called a face of the solid. (vi) An edge forms when two faces meet. (vii) The vertex is the point where three or more edges meet.
Note : A solid is any enclosed three-dimensional shape, i.e., it has 3 dimensions- length, width and height, whereas there are some common (flat) shapes which can be easily drawn on paper. They have only 2 dimensions -length and breadth.
- The plane figures are also called 2-dimensional figures, also written as 2-D.
The table below shows the various types of geometric solids.
2.0Geometric Properties
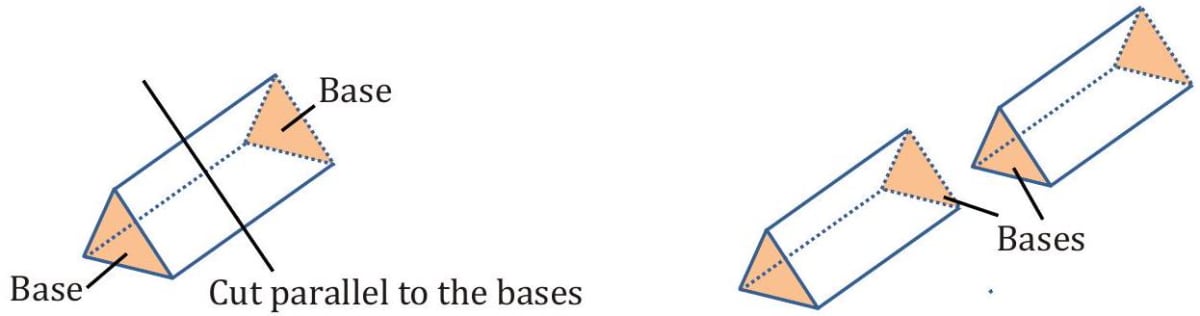
Prism
A prism is a solid with
Properties
(i) The perpendicular distance between the two bases is the height of the prism. (ii) A right prism is a prism in which the bases of the prism are perpendicular to the lateral faces.
Cuboid
A cuboid is a solid with six rectangular faces. Opposite faces have same shapes and sizes.
- If length, breadth and height of cuboid become equal, then it will be a cube.
Cube
A cube is a special type of cuboid with six square faces of the same size. All the edges are equal in length.
Pyramid
A pyramid is a solid with a
Properties
(i) The lateral triangular faces meet at a common vertex. (ii) The perpendicular distance from the common vertex to the base is the height of the pyramid. (iii) A right pyramid is a pyramid in which its vertex is vertically above the centre of the base.
Cylinder
A cylinder is a solid with
Properties
(i) The perpendicular distance between the two bases is the height of the cylinder. (ii) A right cylinder is a cylinder in which the axis is perpendicular to the bases.
- A cylinder has no vertex.
- When term cylinder is used, it is always considered closed cylinder from both ends (3 faces i.e., 2 circular and 1 lateral face).
- Hollow cylinder is open from both the sides (1 lateral face).
Cone
A cone is a solid with
Properties
Sphere
A sphere is a solid in which all points on its curved surface are equidistant from a fixed point which is the centre of the sphere.
Property
The fixed distance from the centre to the surface is its radius.
3.0Euler's formula
If and E are the number of faces, number of vertices and number of edges of a polyhedron then
Q. If then find the value of (no. of edges) of polyhedron.
- Explanation As we know that (given)
4.0Net of Solid Shapes
A net is a flat diagram on one plane that is folded to make a hollow solid. Alternatively, if a hollow solid is opened out, the result is its net. (i) A net is also known as a layout. (ii) The nets of a solid may have different shapes.
Q. Copy each net into your book and add the face that is needed to make the net of the named solid. Shade the added face.
- Explanation
Q. Label each net as of : (i) Cuboid (ii) Cube (iii) Triangular pyramid (iv) Rectangular pyramid (v) Cone (vi) Cylinder (vii) Square pyramid (viii) Triangular prism
- Explanation (i) Cuboid (ii) Rectangular pyramid (iii) Cube (iv) Cylinder (v) Triangular prism (vi) Square pyramid (vii) Triangular pyramid (viii) Cone
5.0Viewing Different Section of a Solid
A solid may be cut vertically, horizontally or obliquely. The cut faces are called cross-sections. Here is a cube which is being cut across. The cross-section of a cube is a square.
By slicing a cube in different planes, we can create differently shaped cross-sections. However, in the case of a cube both a horizontal cut, a vertical cut yield a square. As shown below, the crosssection of the horizontal and vertical cuts of a cuboid are rectangles.
The cross-section of a diagonal cut of a cube is a rectangle.
The figures given below show the cross-sections of an oblique cut of a cube.
Q. Name the shape of the cross-section in each solid?
- Explanation (i) Circle (ii) semicircle (iii) Triangle (iv) Circle (v) Circle (vi) Rectangle (vii) Triangle (isosceles) (viii) Triangle (isosceles)
6.02-D representations of 3-D Shapes
The pictures given below show the two-dimensional drawings of a car which is a threedimensional object.
We can use 2-D representations of 3-D shapes to help us to visualise them. A solid can be viewed from different directions, i.e., from above, from front, from side. We can use these views to visualise what the whole solid looks like.
The simplest example is that of a cube. The cube has a square as a shape when viewed from the given directions. The diagram shows a solid.
Special names are given to the views from different directions. (i) Plan of a solid is the view seen when looking down from above. (ii) Front elevation is the view seen from the front. (iii) Side elevation is the view seen from the side.
Q. Draw the above, front and side elevations of following solids.
- Explanation
Q. Sketch the rectangular pyramid as shown as if seen directly from
- Explanation
(i)
(ii)(iii)view from the side
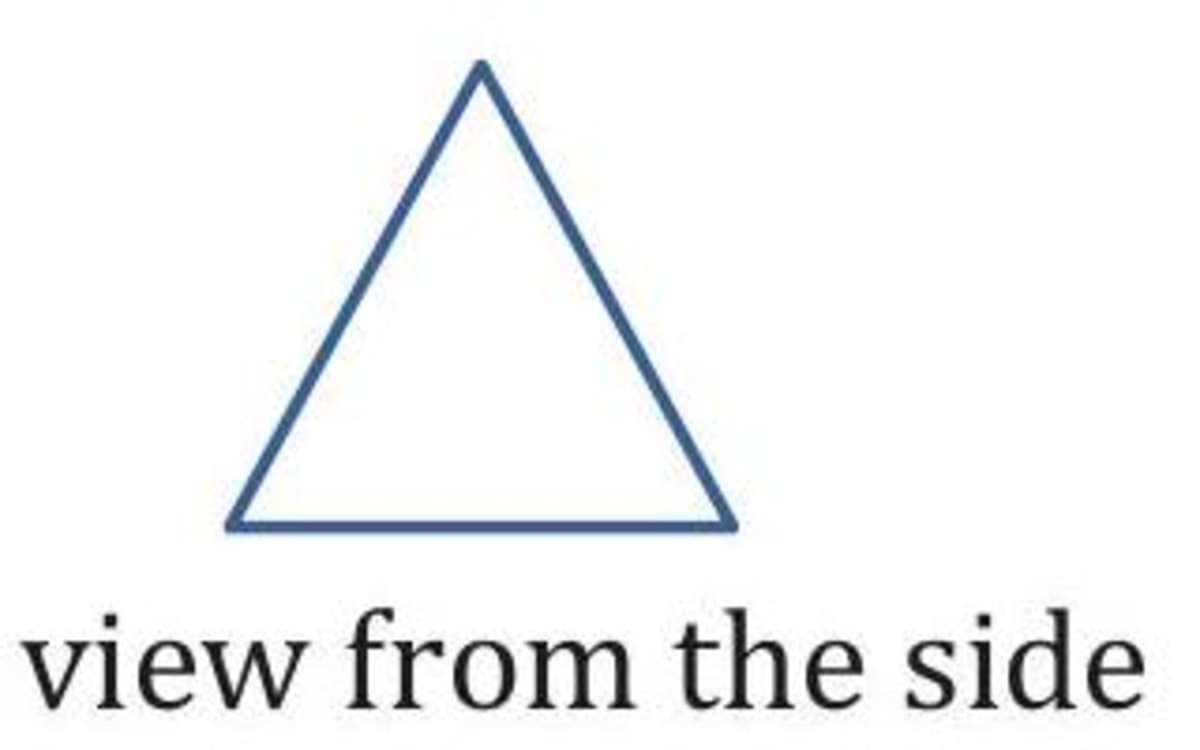
Q. The diagram given below shows a solid, made of cubes drawn on a dotted (isometric) paper. Draw its plan, front and side elevations.
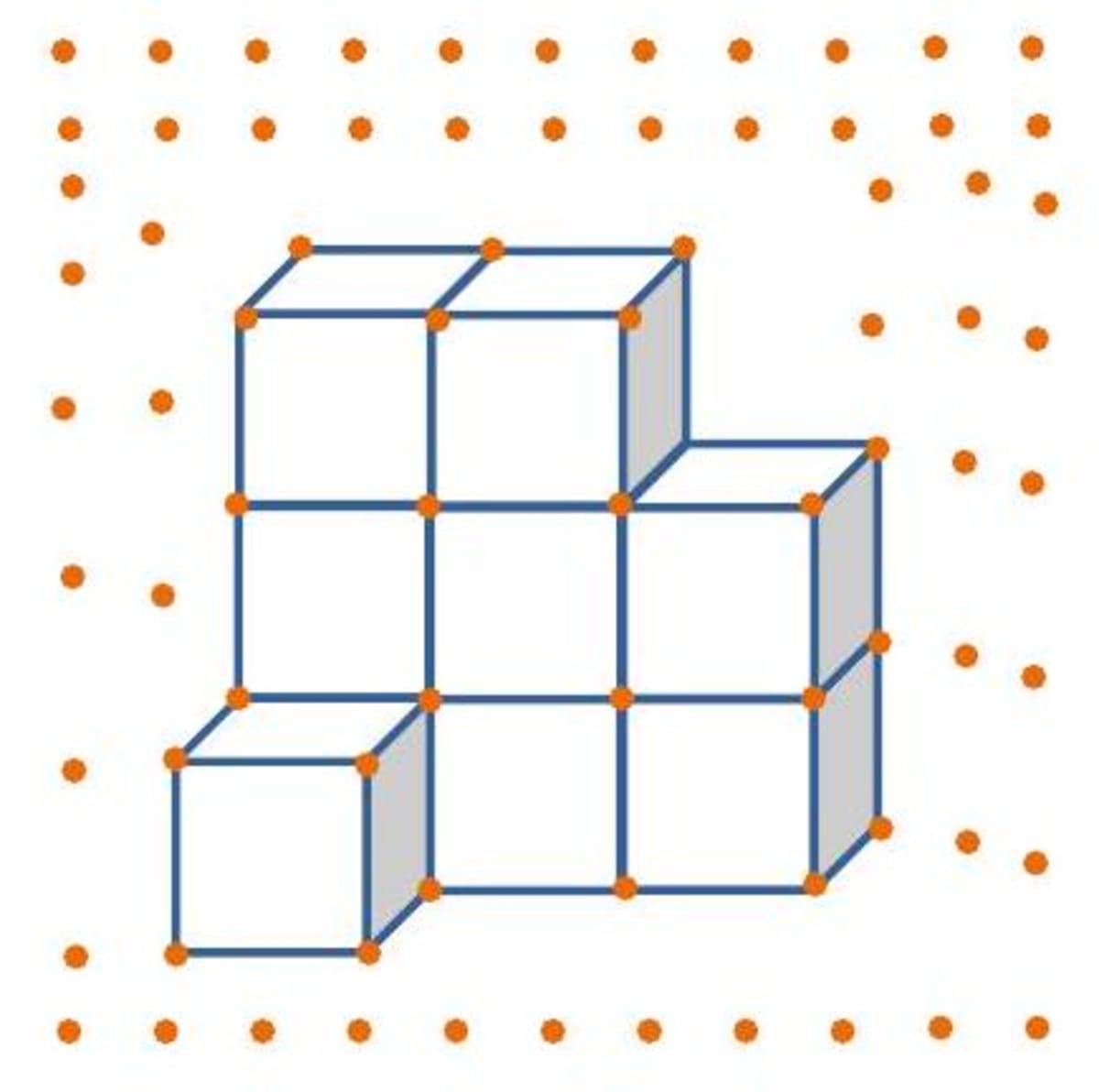
- Explanation
Visualising solid shapes (Representing 3-D in 2-D)