Integers

1.0The need of negative numbers
As we know that when a smaller whole number is subtracted from larger whole number we get a whole number but what about etc...? Clearly there are no whole numbers to represent them. So, there is a need to extend our whole number system to represent the above differences. Corresponding to natural number , we introduce new numbers denoted by . , respectively such that , and so on. The oppositeness of two quantities may be indicated by representing one as a positive and the other as a negative number. We say that -1 and 1 are the opposites of each other; -2 and 2 are the opposites of each other; -3 and 3 are the opposites of each other, and so on.
2.0Integers
Integers were introduced by Arbermouth Holst in 1563. Numbers greater than 0 are called positive numbers. Extending the number line to the left of 0 allows us to picture negative numbers those are less than 0 . When a single + sign or no sign is in front of a number, the number is a positive number. When a single - sign is in front of a number, the number is a negative number. -5 indicates "negative five". 5 and +5 indicates "positive five". The number 0 is neither positive nor negative.
3.0Representing integers on number line
Integers can be represented on a number line. The symbol for integer is Z and Z stands for Zahlen which is German word. The number line shows that every integer has an opposite number except ' 0 '. The numbers .... are positive numbers, denoted by +Z . The numbers ..... are negative numbers, denoted by . The positive and negative integers together with 0 are integers, denoted by Z or I . thus

4.0Comparing the values of two integers
Number line can be used to compare the values of two integers.
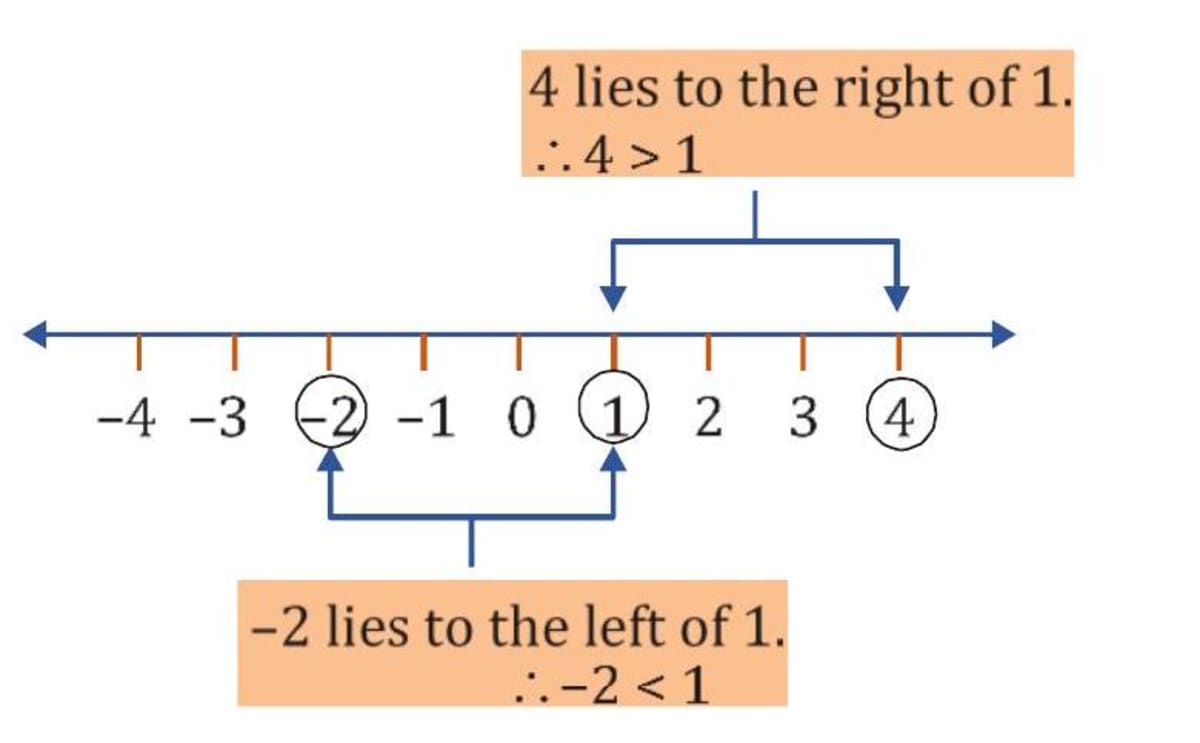
Horizontal number line
(i) On a horizontal number line, an integer is greater than the integer on its left. (ii) On a horizontal number line, an integer is less than the integer on its right.
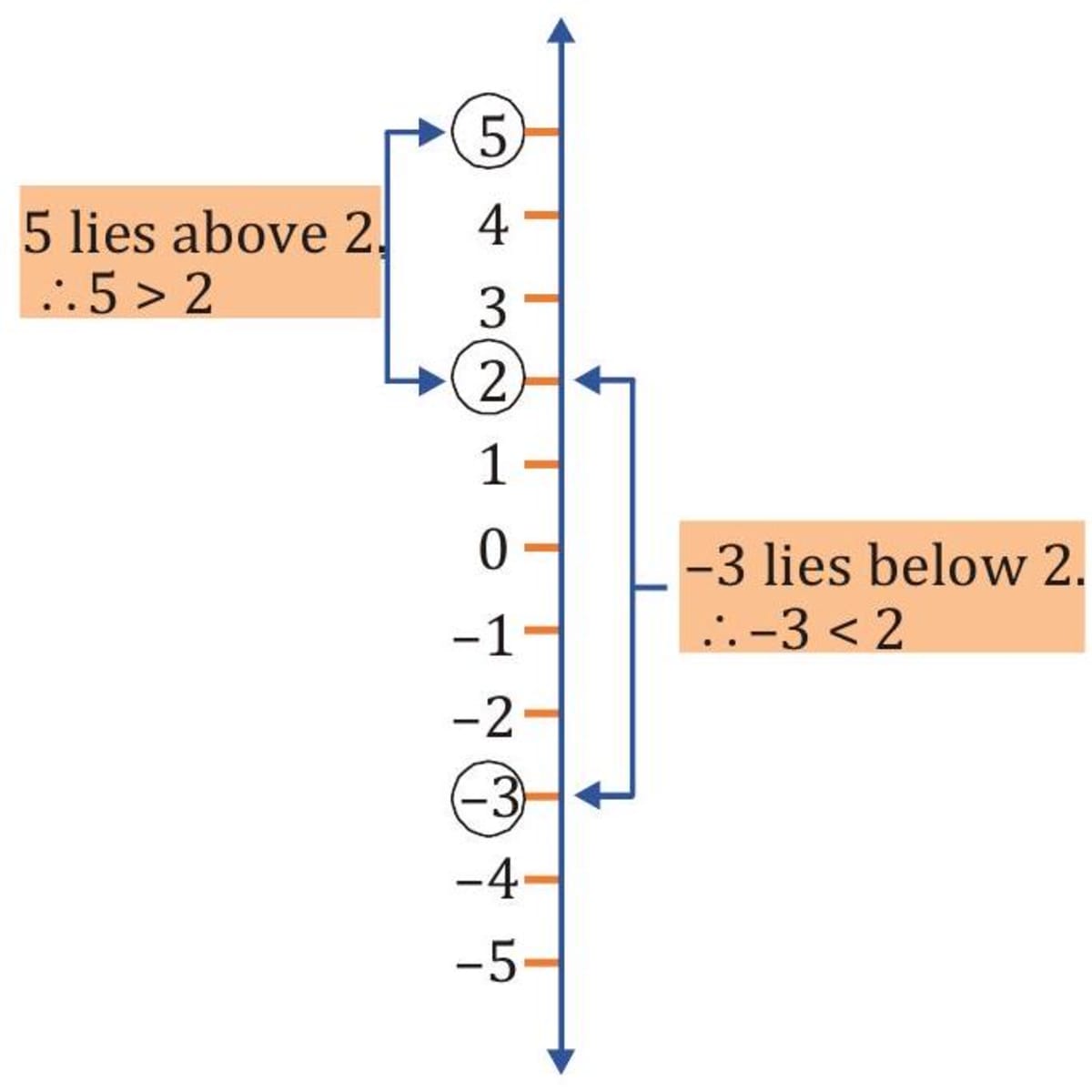
Vertical number line
(i) On a vertical number line, an integer is greater than the integer below it. (ii) On a vertical number line, an integer is less than the integer above it.
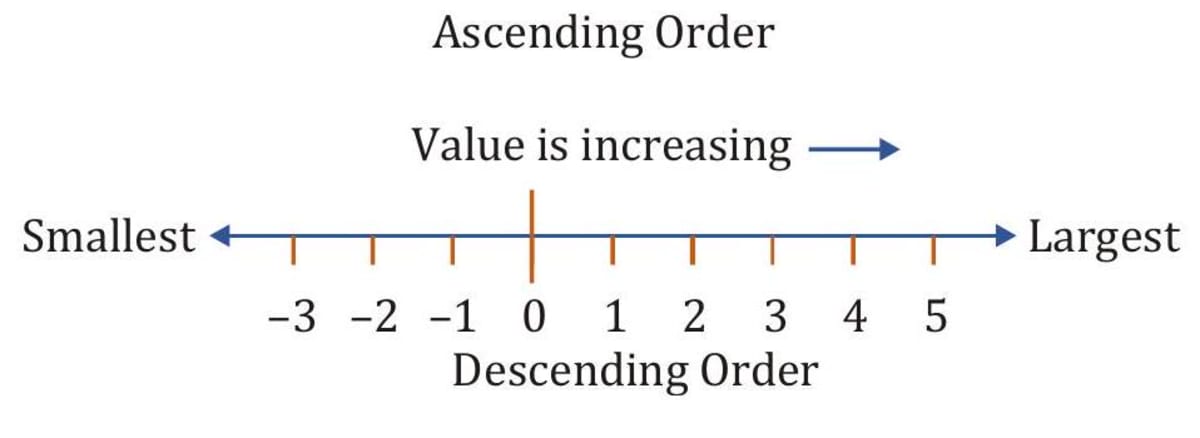
Arranging integers in order
(i) Number lines can be used to arrange the order of integers in increasing or decreasing order. (ii) The value of integers on a horizontal number line increases from left to right and decreases from right to left.
Negative numbers were finally accepted into the number line in the nineteenth century.
- Two integers are opposite, if they are on the same distance away from zero, but on opposite sides of the number line.
- There is no such thing as the lowest or largest integer. 1 is the lowest positive integer, and -1 is the largest negative integer.
Writing positive and negative integers to represent word descriptions
A positive or negative number is used to denote
I. An increase or decrease in value For e.g., (i) Rs. 70 withdrawn is denoted by -Rs. 70. (ii) Rs. 70 deposited is denoted by + Rs. 70.
II. Values more than zero or less than zero For e.g., (i) denotes a temperature that is below . (ii) denotes a temperature that is above .
III. A positive direction or a negative direction (opposite direction) For e.g., (i) 5 m denotes a direction 5 m to the right. (ii) -5 m denotes a direction 5 m to the left.
IV. Position above or below sea level

- Positive integers may be written with or without a sign.
- Remember that positive integers represent gains, or deposits, and negative integers represent losses, or withdrawals.
5.0Operations on integers
Using number line-
Addition of integers
You know how to use the number line to add whole numbers. You can also use the number line in the same way to add positive and negative numbers. (i) Adding two positive integers. For e.g., add 3 and 2

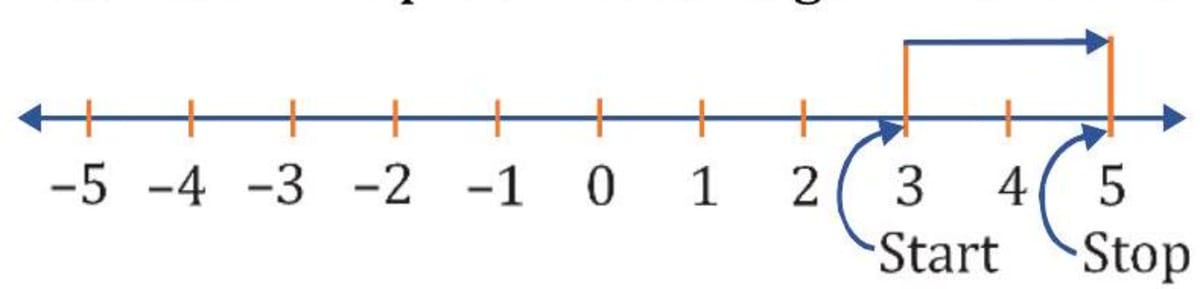
(ii) Adding two negative integers For e.g., add - 3 and - 2

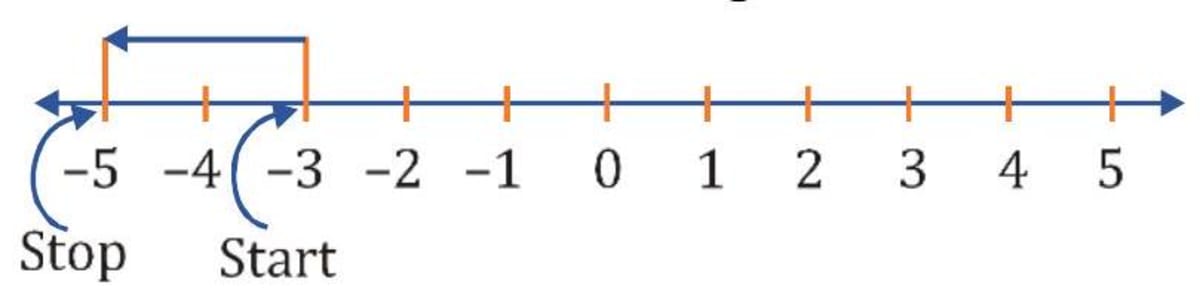
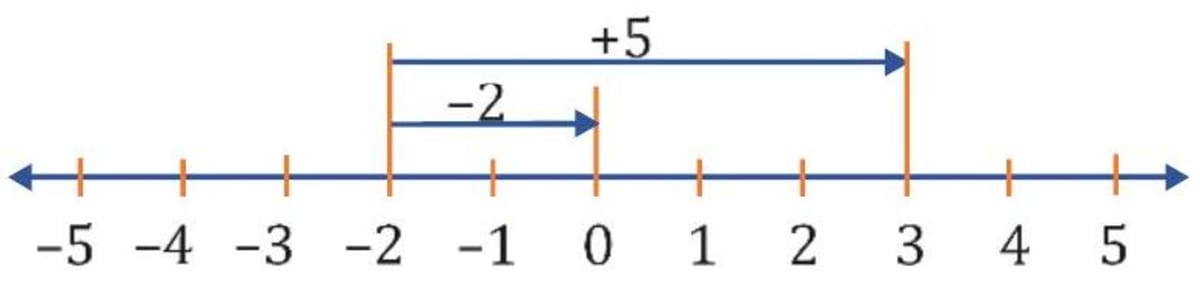
(iii) Adding a positive integer and a negative integer For e.g., add - 2 and 5
Using basic operation
Rule 1: To add two integers of like signs, find the sum of their absolute values and place the common sign before the sum. E.g.
Rule 2: To add two integers of unlike signs, find the difference of their absolute values and place the sign of the integer which has the larger absolute value before this difference. E.g. E.g.
General mistake by student
- , not 50
Subtraction of integers
If and are two integers then is equal to , i.e., to subtract from , change the sign of and add to . Rule: (i) Change the sign of the subtrahend. (ii) Add by the rules for adding integers.
In general, 'a-b' means the displacement from the point of to the point of . Eg. (i)
(ii)
Rule of signs in addition and subtraction
If is any number, then The sign of the number inside the brackets remains unchanged if there is a positive sign before it. The sign of the number inside the bracket changes if there is a negative sign before it.
6.0Properties of Integers
Additive Inverse
If and are three integers then and The sum of an integer and its opposite is 0 . Thus, if is an integer then a and -a are called opposites or negatives or additive inverses of each other.
Successor and predecessor of an integer
Let be an integer then is called the successor of a and is called the predecessor of a. Eg. The successor of -18 is and the predecessor of .
7.0Numerical Ability
Use a number line to answer the following questions. (i) Which number shall we reach if we move 5 numbers to the left of 3? (ii) Which number shall we reach if we move 6 numbers to the right of -3 ?
- Explanation
(i)
Moving 5 numbers to the left of 3 , we reach the point -2 . (ii)
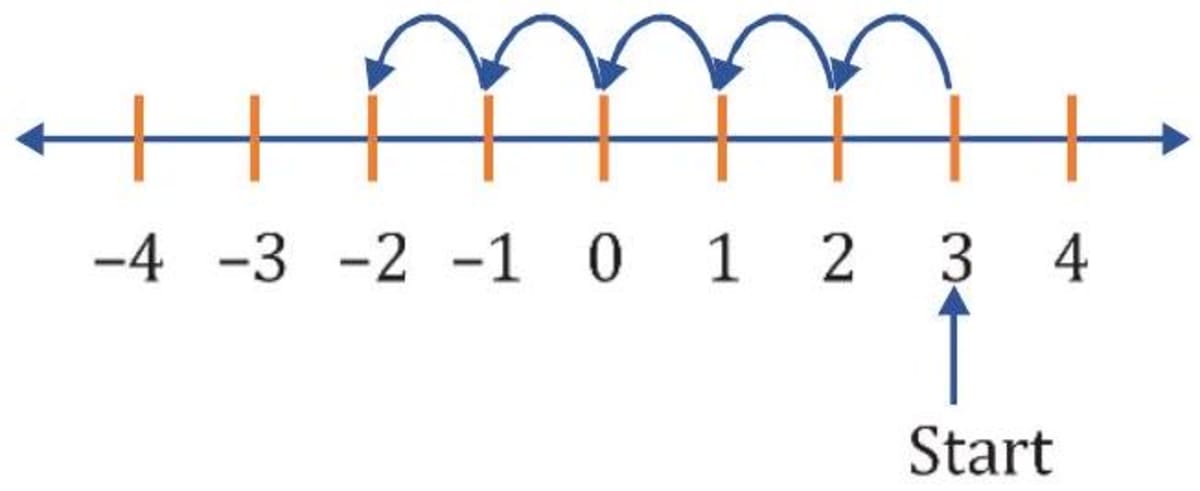 Moving 6 numbers to the right of -3 , we reach the point 3 .
Moving 6 numbers to the right of -3 , we reach the point 3 .
Fill in the blanks by the appropriate symbol ' ' or ' ' in each of the following cases. (i) 0 0...... 3 (ii) -7...... 0 (iii) 7......-5 (vi) -3 ......-8
- Explanation (i) 0 ...... 3 Since 0 is less than 3 and on the left hand side of 3 . . (ii) -7 is on the left side of 0 so it is less than 0 . . (iii) 7......-5. -5 is less than 7 and 7 is on the right hand side of -5 . . (vi) -8 is on the left side of -3 . .
Represent the integers on the number line.
- Solution
Draw a number line and show the points corresponding to the integers , and -2 by the dots.
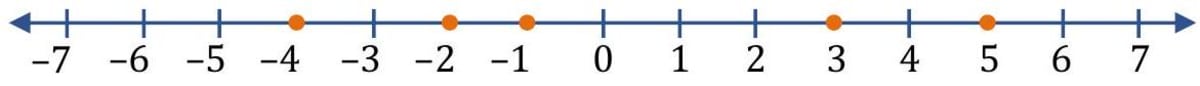
Write the numbers in the following situations with appropriate sign. (i) 100 m below sea level (ii) A gain of Rs. 600
- Explanation (i) 100 m below sea level. Since, it is below sea level, the sign will be negative. Therefore, it can be written as -100 m . (ii) A gain of Rs. 600. A gain indicates that the sign will be positive. Therefore, it can be written as + Rs. 600 .
Write the opposite of the following: (i) Withdrawn of Rs. 1000 (ii) 50 km North (iii) temperature falls (iv) Won by 2 seconds
- Solution (i) Deposit of Rs. 1000 (ii) 50 km South (iii) temperature increase (iv) Lose by 2 seconds
Add the following : (i) (ii) (iii)
- Explanation (i) (ii) (Find and since and it is a negative integer, the answer will also be negative.) (iii) (Add the absolute values and place the common sign which is negative or minus sign in the answer.)
Add the following : (i) (ii) (iii) (iv) (v) (vi) (vii) (viii)
- Solution (i) (Add as both the numbers have the same sign.) (ii) (iii) (iv) (Subtract as both the numbers have different signs.) (v) (vi) (Subtract as both have opposite signs.) (vii) (Add as both have the same sign.) (viii) Add as both have the same sign
(i) Find the additive inverse of 70 and -1002. (ii) Find the successor and predecessor of . (iii) Find an integer a such that (a) (b)
- Explanation (i) The additive inverse of 70 is -70 and -1002 is 1002 . (ii) The successor of -39 is . The predecessor of -39 is . (iii) (a) (b)
Find the sum of the successor and additive inverse of 452.
- Solution Successor of 452 is Additive inverse of Sum of successor and additive inverse of
Shyam has overdrawn his checking account by Rs.38. The bank debited him Rs. 20 for an overdraft fee. Later, he deposited Rs.150. What is his current balance? Explanation Total amount deposited= Rs. 150 Amount overdrew by Shyam= Rs. 38 Debit amount [Debit is represented as negative integer] Amount charged by bank= Rs. 20 Debit amount Total amount debited Current balance= Total deposit + Total Debit [Subtract and give the sign of greater number] Hence, the current balance is Rs. 92.
Anna is a microbiology student. She was doing research on optimum temperature for the survival of different strains of bacteria. Studies showed that bacteria need optimum temperature of while bacteria Y need optimum temperature of . What is the temperature difference?
- Solution Bacteria X need optimum temperature Bacteria Y need optimum temperature Temperature difference [Subtract and give the sign of greater number] Hence, temperature difference is .
A submarine submerges at the rate of . If it descends from above the sea level, how long will it take to reach 250 m below sea level?
- Solution Initial position (above sea level) Final position Total depth it submerged negative sign shows that the submarine travelled below sea level. Thus, the submarine travelled 270 m below sea level. Time taken to submerge 1 meter minutes Time taken to submerge Time Hence, the submarine will reach 250 m below sea level in 54 minutes.
The diagram below shows a pendulum tied to a string. (i) When the pendulum was released from the table, it dropped to a height of 80 cm below the table. It was then pulled 35 cm up. How far is the pendulum from the table now? (ii)The temperature of a town is at night. During the day, the temperature increases by . What is the temperature of the town during the day?
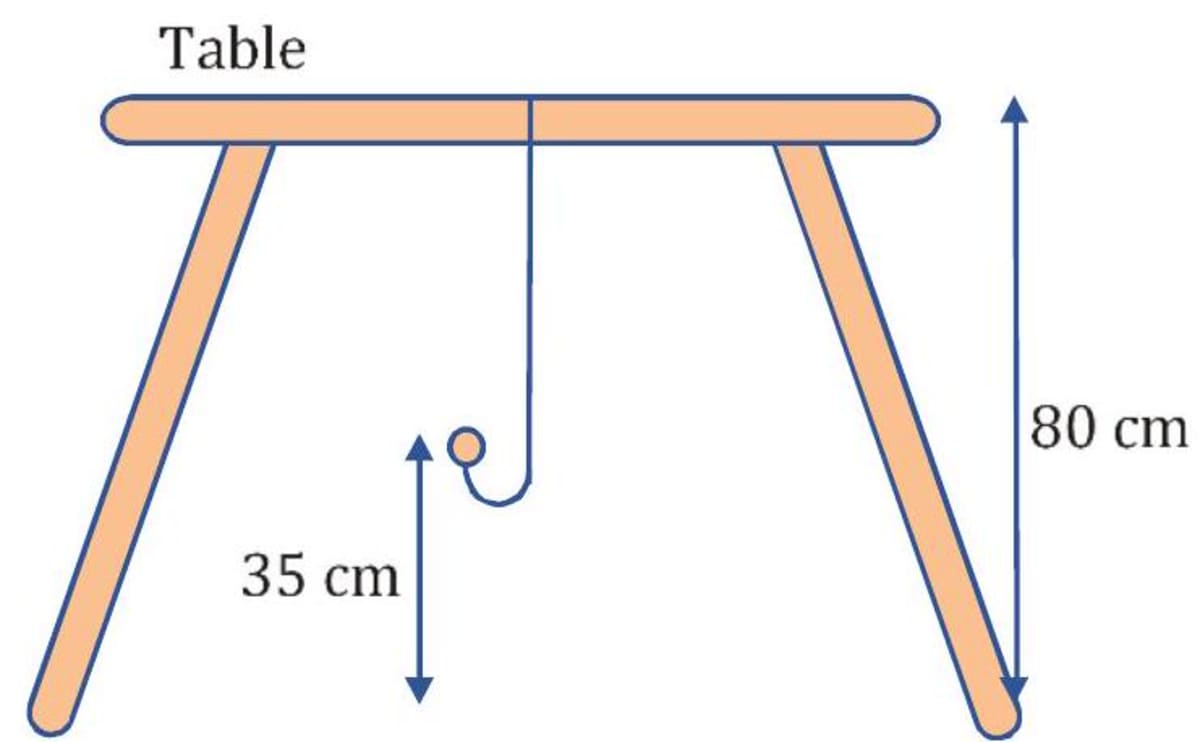
- Solution (i) The distance of the pendulum from the table The pendulum is 45 cm below the table. (ii) The question involves the sum of negative integer and a positive integer. The temperature of the town during the day is .
Subtract: (i) - 8 from 5 (ii) 8 from 5 (iii) - 8 from - 5 (iv) 8 from - 5
- Explanation
(i)
Step 1. Change the sign of -8 . It becomes +8 .
Step 2. Add 8 to 5
You can show it on the number line as under
Start at -8 and find the displacement from -8 to 5 . To arrive at 5 , you have to move 13 units in the positive direction. (ii) Step 1. Change the sign of 8 . You get -8 . Step 2. Add 5 to -8 On the number line, start at 8 and move so as to arrive at For this you have to move 3 units in the negative direction.
 The two integers which are opposite of each other are called additive inverse of each other as their sum is zero. (iii) Step 1. Change the sign of -8 . It becomes +8 . Step 2. Add 8 to -5 On the number line, start at -8 and move so as to arrive at -5 . For this you have to move 3 units in the positive direction.
The two integers which are opposite of each other are called additive inverse of each other as their sum is zero. (iii) Step 1. Change the sign of -8 . It becomes +8 . Step 2. Add 8 to -5 On the number line, start at -8 and move so as to arrive at -5 . For this you have to move 3 units in the positive direction.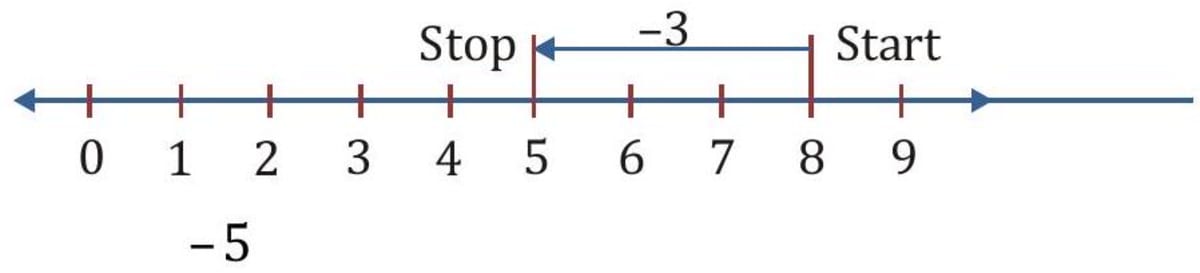 (iv) Step 1. Change the sign of 8 . You get -8 . Step 2. Add -8 to -5 On the number line, start at 8 and move so as to arrive at -5 . For this you have to move 13 units in the negative direction.
(iv) Step 1. Change the sign of 8 . You get -8 . Step 2. Add -8 to -5 On the number line, start at 8 and move so as to arrive at -5 . For this you have to move 13 units in the negative direction.

Subtract the sum of 837 and from the sum of and 792 .
- Explanation Sum of 837 and Sum of -392 and Now 400-350=50
The sum of two integers is . If one of them is , determine the other.
- Solution Sum of two integers other integer other integer sum
Find the value of .
- Solution
Find the value of .
- Solution
Related Article:-
Join ALLEN!
(Session 2026 - 27)