Symmetry

• In our daily to day life we come across many items, which have looking exactly a like.

1.0Symmetry

If we fold a picture in half and both the halves-left half and right half-match exactly then we can say that the picture is symmetrical. Eg.- India Gate and Red Fort in Delhi, Taj Mahal in Agra, are all symmetrical monuments. Symmetry is different types, such as reflection symmetry, line symmetry, rotational symmetry etc.

2.0Transformation

Transformation geometry shows how shape changes position and size according to certain rules. Some of the most common mathematical transformations are reflection (flips), rotations (turns), translation (sliding without turning), and enlargement or reductions (making larger or smaller).

3.0Line Symmetry

A shape is symmetrical if one part of the object appears identical to the other part (mirror image).

If a figure can be drawn on paper in such a way that if the paper is folded in half, the two halves of the figure exactly cover each other, then the shape is symmetric. The line of fold is the axis of symmetry.

A shape has symmetry if you can fold it so that one side fits exactly on to the other. The fold line is the line of symmetry. A line of symmetry is also called a mirror line. The two halves of a symmetrical body exactly match in shape and size.

Linear symmetry in some common geometrical shapes

• Lines :A line has an infinite number of symmetry lines, all perpendicular to it. The line itself coincides with its image.
  
• Segments : A segment has two symmetry lines, its perpendicular bisector and the segment itself.
  
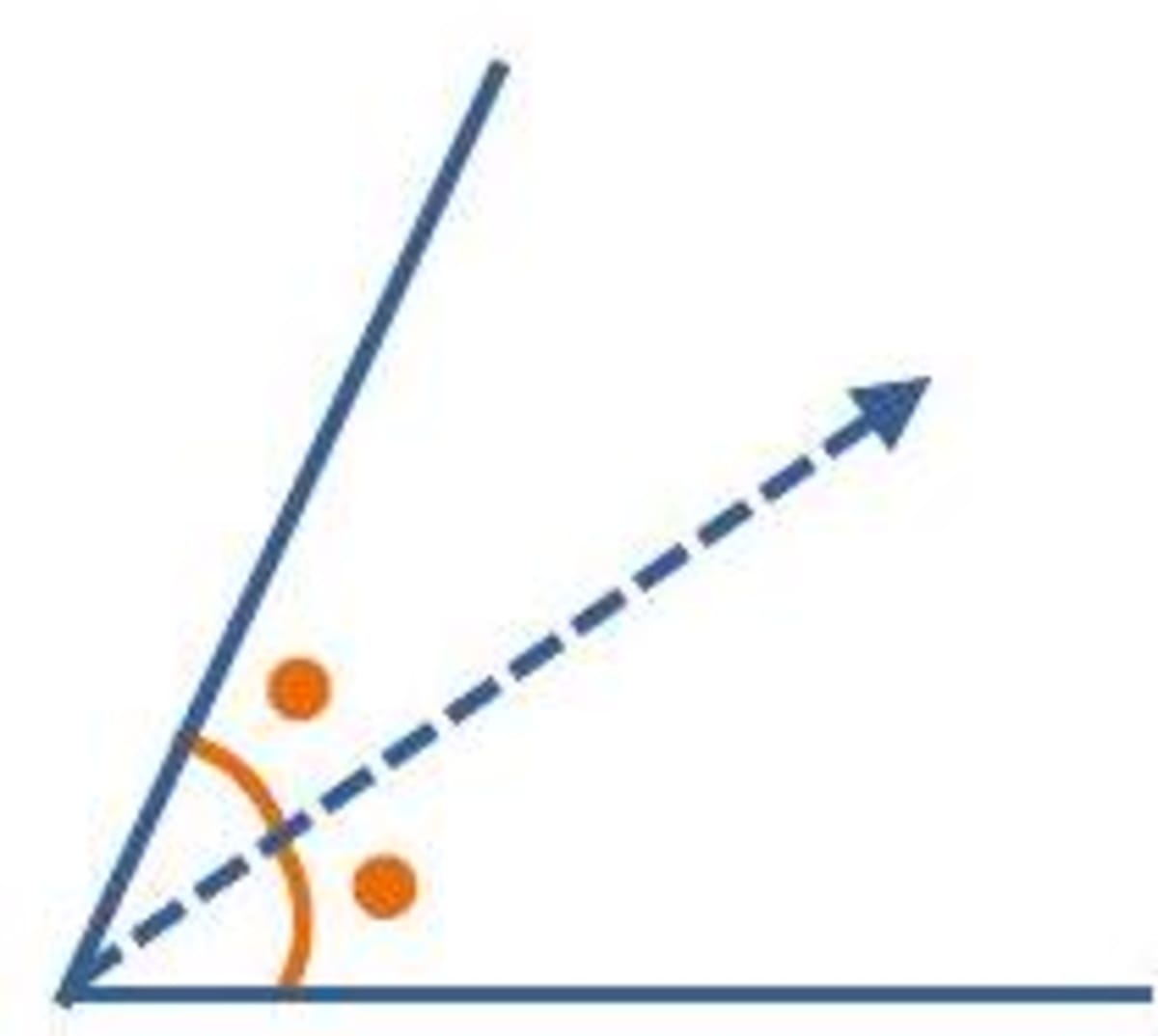
• Angles : An angle has one symmetry line. The angular bisector of the angle is the line of symmetry. Lines of symmetry are shown by dotted lines.
  
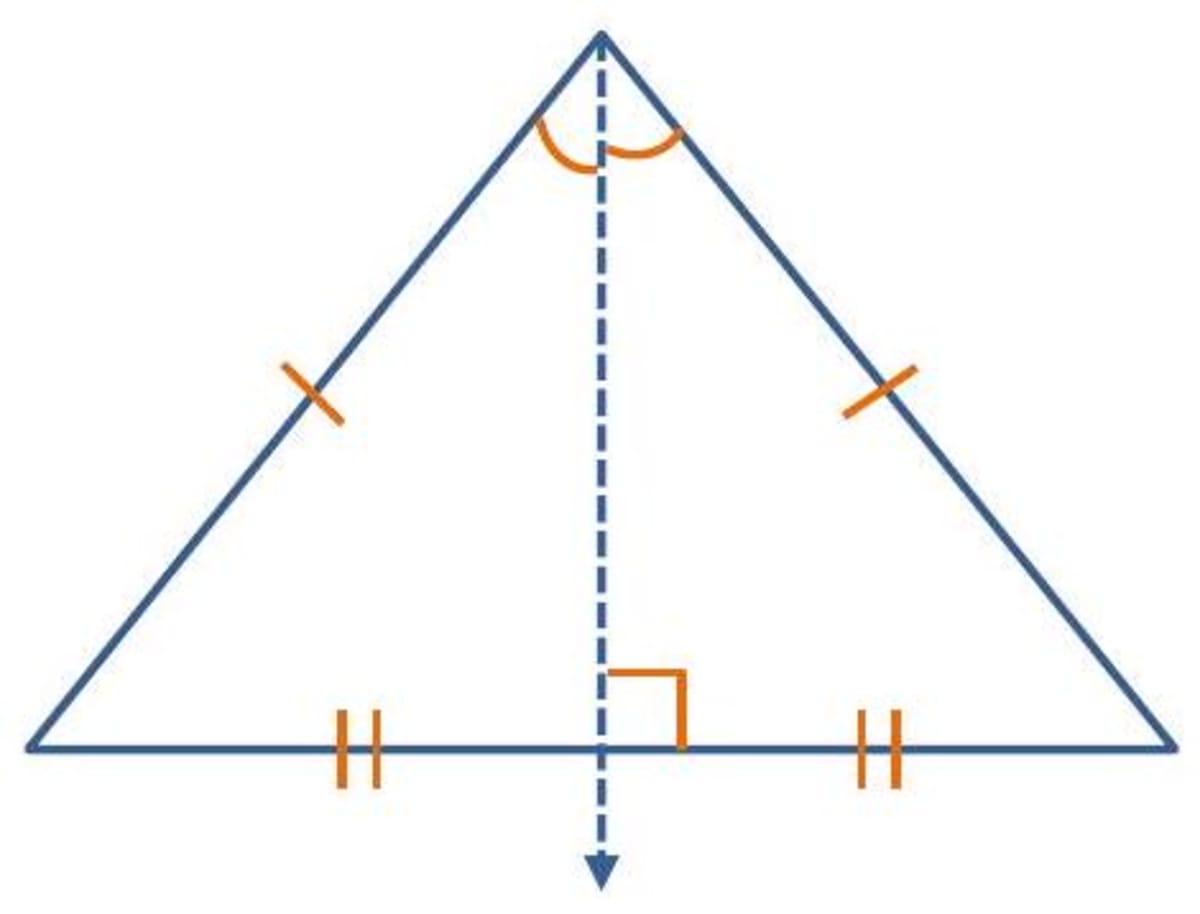
• Isosceles triangle : An isosceles triangle has one symmetry line, the angular bisector of the vertex, which is also the perpendicular bisector of the base.
  
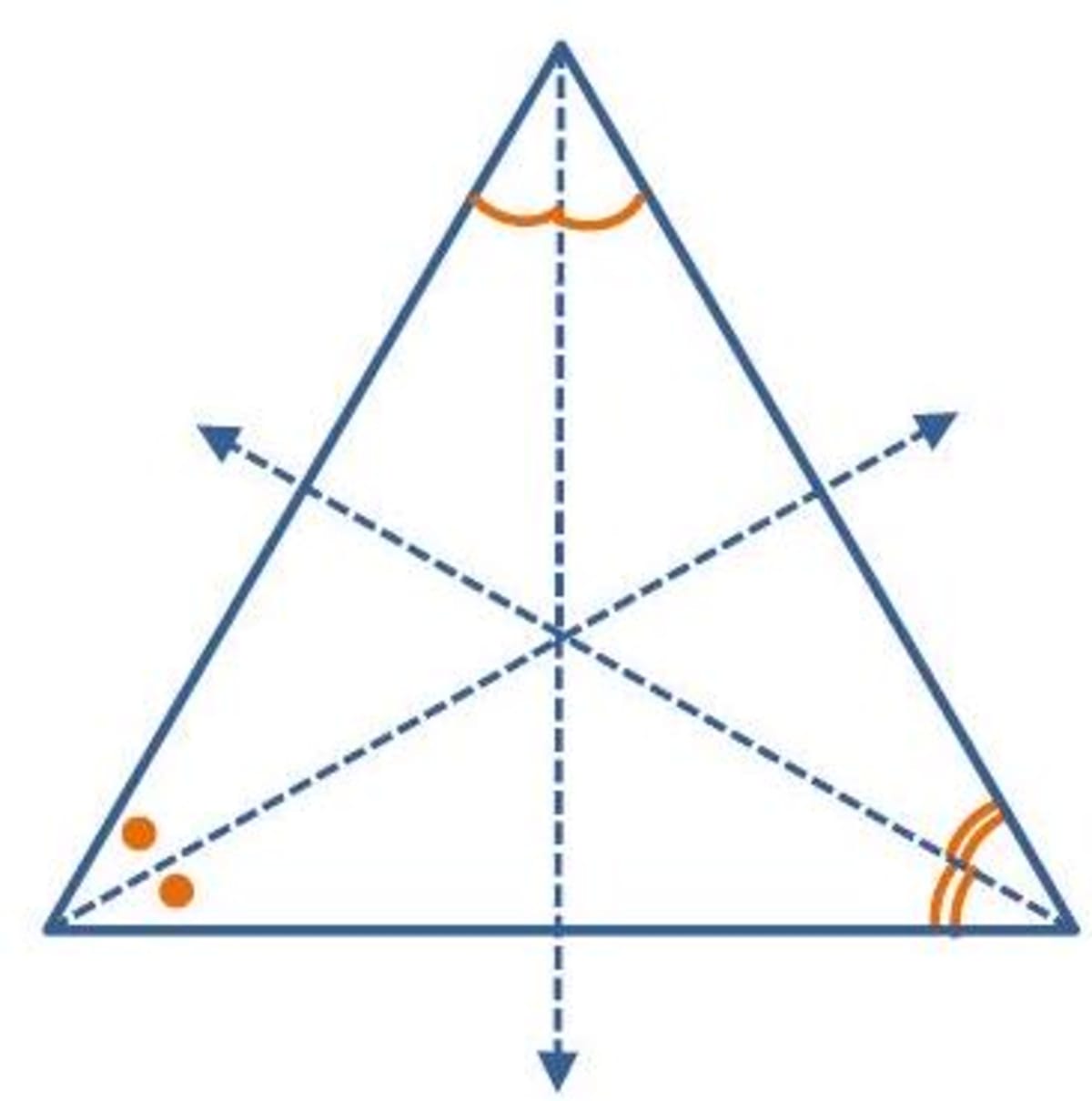
• Equilateral triangles : An equilateral triangle has three symmetry lines, the angular bisector of each of the vertices.
  
• Isosceles trapezium : An isosceles trapezium has one symmetry line, the perpendicular bisector of the parallel sides.
  
• Kites and arrowheads: One of their diagonals is a symmetry line.
  
• Rhombus : The two diagonals of a rhombus are its two lines of symmetry.
  
• Rectangles : A rectangle has two symmetry lines - the perpendicular bisectors of each pair of opposite sides.
  
• Squares: A square has four symmetry lines, the two diagonals and the perpendicular bisectors of each pair of opposite sides.
  
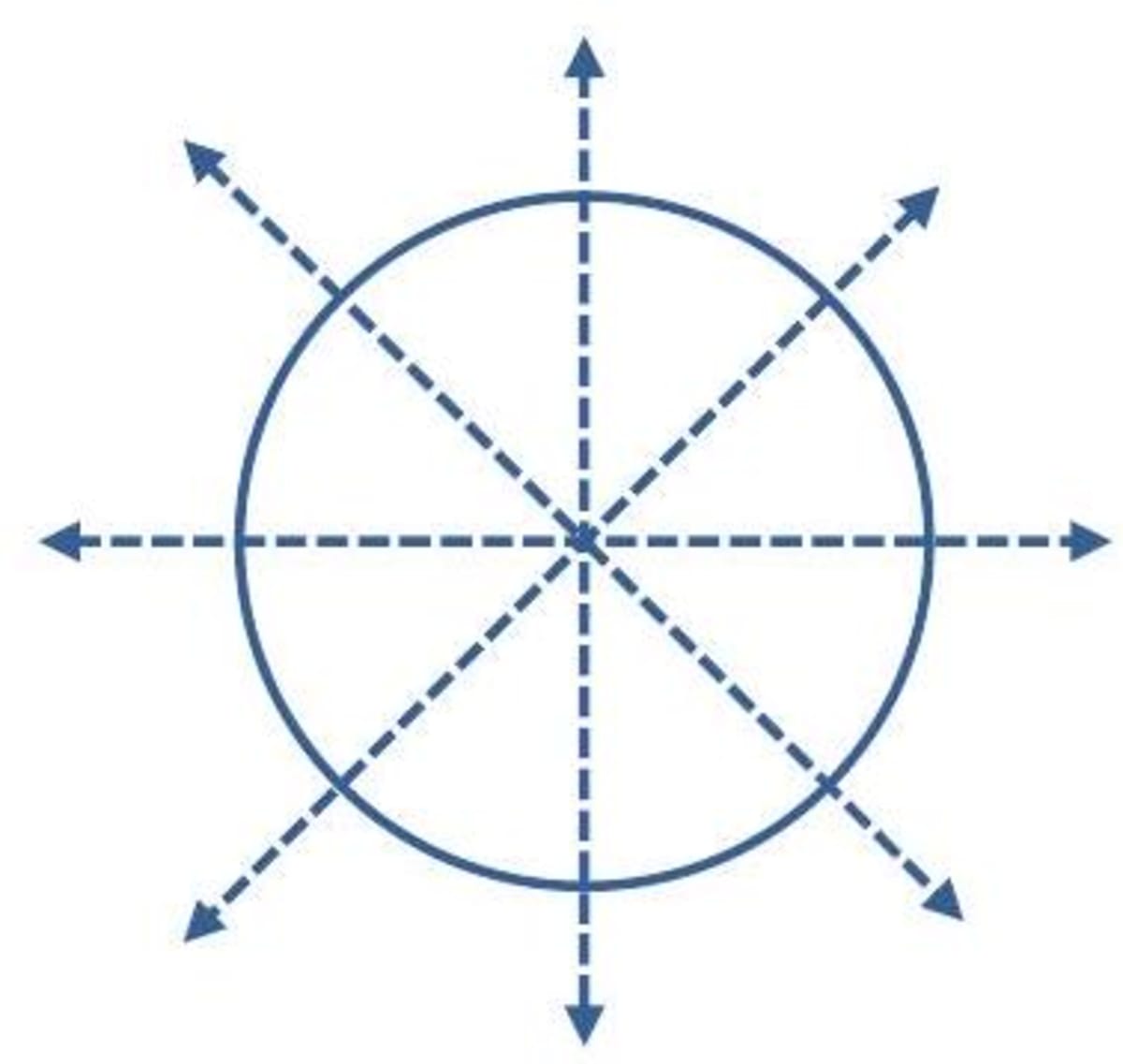
• Circles: A circle has an infinite set of symmetry lines through the centre (diameters).
  

Symmetry of letters of the alphabet

The following letters of the English alphabet are symmetrical about the dotted line (or lines).

The following letters have no line of symmetry.

The concept of line of symmetry is closely linked to the concept of reflection. You already know that the line of symmetry is also called the mirror line.

4.0Reflection symmetry (Mirror symmetry)

The effect of a mirror is to produce an image of the same shape and size but in the opposite direction. This is called a reflection. Reflection symmetry has the same effect as a mirror. A reflection in a line produces a mirror image. In a reflection, the image is of the same size and each point on it is at the same perpendicular distance from the axis of reflection as the corresponding point on the object.

A point ${\mathrm{P}}^{\prime }$ is called the image of a point P in a line $\ell$, if $\ell$ is the perpendicular bisector of the line segment ${\mathrm{PP}}^{\prime }$. The transformation $\mathrm{P}\to {\mathrm{P}}^{\prime }$ is called the reflection in $\ell$.

(i) The line ' $\ell$ ' is called the mirror line. (ii) All points on line $\ell$ are their own images. (iii) The length and angle measures remain unchanged under reflection. (iv) The image of a figure under reflection is congruent to original figure. (v) Perpendicular and parallel lines reflect into perpendicular and parallel lines respectively.

Reflection in x-axis

A point $P(a,b)$ has its image $P^{\prime }(a,-b)$, when reflected in $x$-axis $(y=0)$.

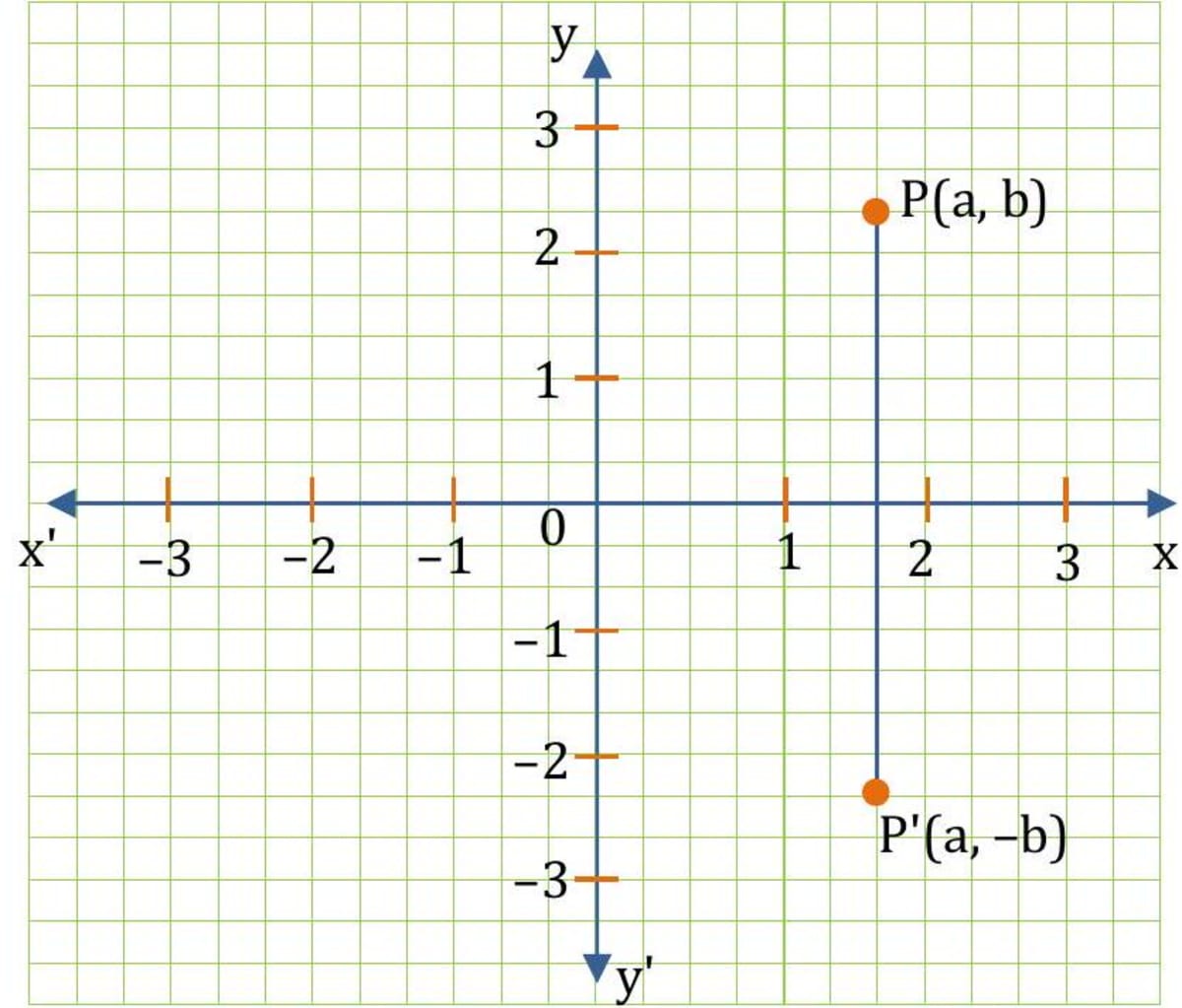
Reflection in y-axis

A point $P(a,b)$ has its image $P^{\prime }(-a,b)$, when reflected in $y$-axis $(x=0)$.

5.0Rotational symmetry

Rotation is the movement (turning) of an object about a point through a given number of degrees in a clockwise or an anticlockwise direction. The below figure shows a rotation of $90^{\circ }$ in clockwise direction about the point 0 .

The direction in which the hands of a clock rotate is called clockwise. The opposite direction of rotation is called anticlockwise.

Centre of rotation and angle of rotation

When an object rotates, its shape and size do not change. The rotation turns an object about a fixed point. This fixed point is called the centre of rotation.

The angle of turning during rotation is called the angle of rotation. A full turn, means a rotation of $360^{\circ }$. A half turn is a rotation of $180^{\circ }$ and a quarter turn is a rotation of $90^{\circ }$.

Rotation through 90^{\circ}

Plot a point on a graph-paper and rotate the graph paper through $90^{\circ }$ about the origin 0 . (i) When rotated through $90^{\circ }$ anticlockwise, point $\mathrm{P}(\mathrm{a},\mathrm{b})$ takes the position ${\mathrm{P}}^{\prime }(-\mathrm{b},\mathrm{a})$. (ii) When rotated through $90^{\circ }$ clockwise, point $\mathrm{P}(\mathrm{a},\mathrm{b})$ takes the position ${\mathrm{P}}^{\prime \prime }(\mathrm{b},-\mathrm{a})$.

Rotation through 180^{\circ}

Plot a point on a graph-paper and rotate the graph-paper through $180^{\circ }$ about the origin 0 . When rotated through $180^{\circ }$, the point $\mathrm{P}(\mathrm{a},\mathrm{b})$ takes the position ${\mathrm{P}}^{\prime }(-\mathrm{a},-\mathrm{b})$. Both directions of rotation (clockwise/anticlockwise), produces the same result.

6.0Line symmetry and rotational symmetry

We now discuss the symmetry of some geometrical shapes which have both line of symmetry as well as rotational symmetry.

A square

It is clear from the following that the square ABCD when rotated about the point 0 through $90^{\circ }$, $180^{\circ },270^{\circ }$ and $360^{\circ }$ will fit exactly each time onto itself. So, it has a rotational symmetry of order 4. Also, it has 4 lines of symmetry, namely, the diagonals and the lines joining the mid-points of opposite sides.

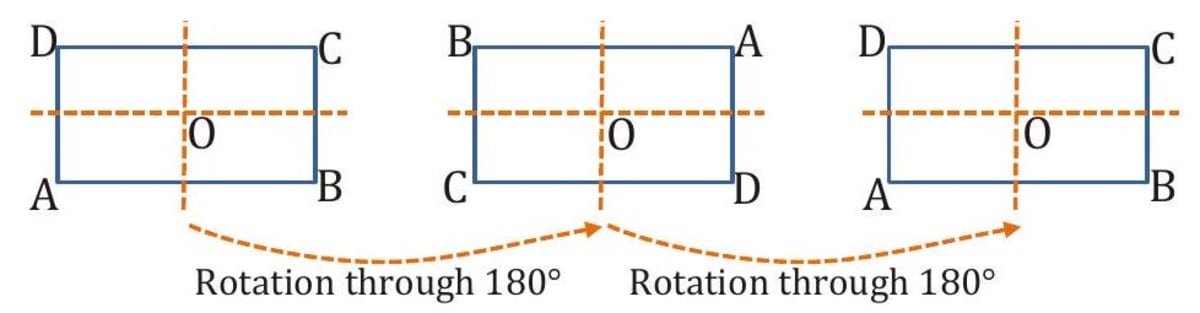
A rectangle

As shown below a rectangle ABCD fits exactly each time onto itself when rotated about 0 through $180^{\circ }$ and $360^{\circ }$. So, it has rotational symmetry of order 2 . Also, it has 2 lines of symmetry.

An equilateral triangle

An equilateral $△\mathrm{ABC}$ fits exactly each time onto itself when rotated through $120^{\circ },240^{\circ }$ and $360^{\circ }$ about the centroid 0 . So, it has rotational symmetry of order 3 . Also, it has three lines of symmetry along the bisectors of interior angles of the triangle.

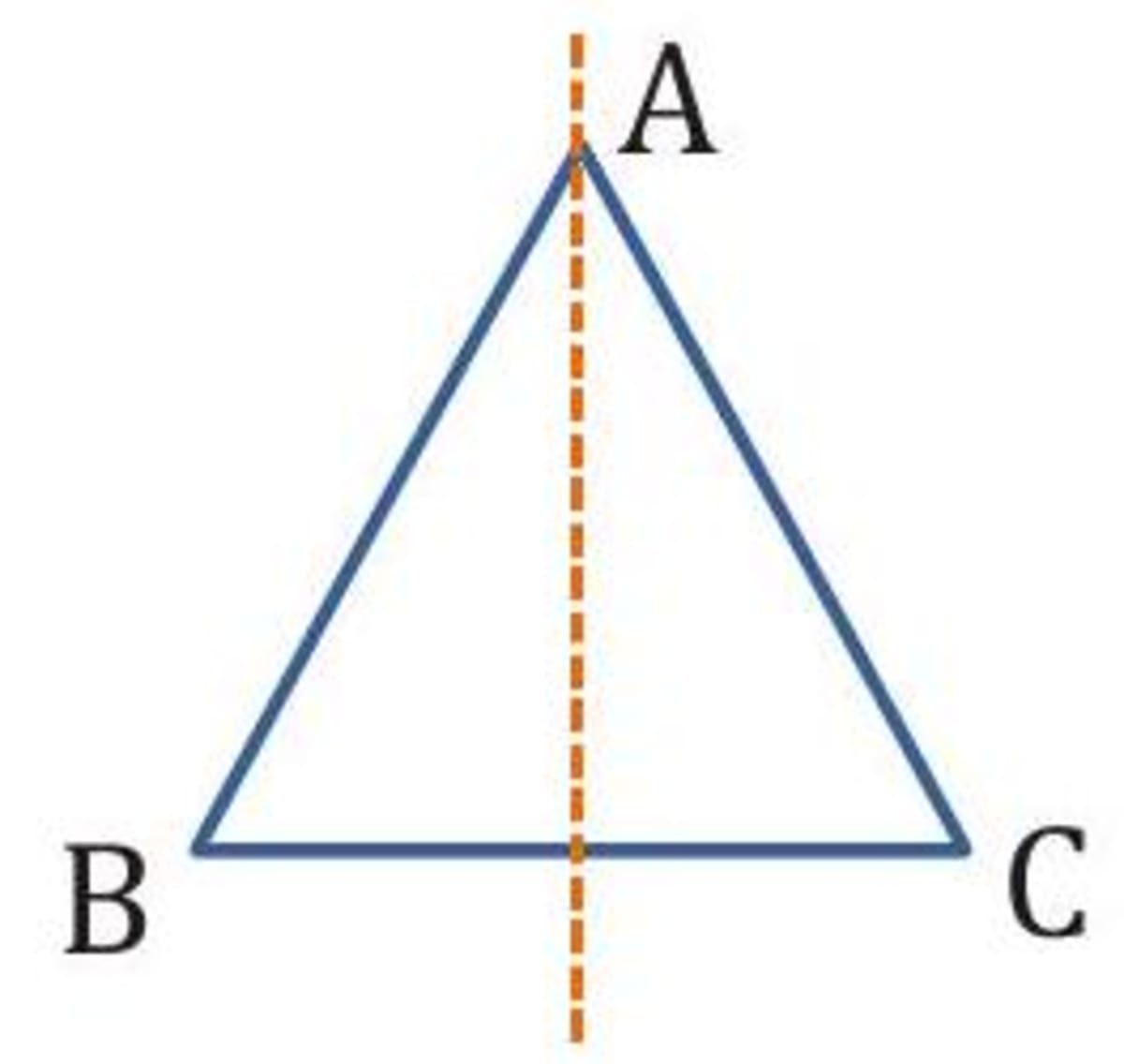
An isosceles triangle

It has a line of symmetry but does not have rotational symmetry.

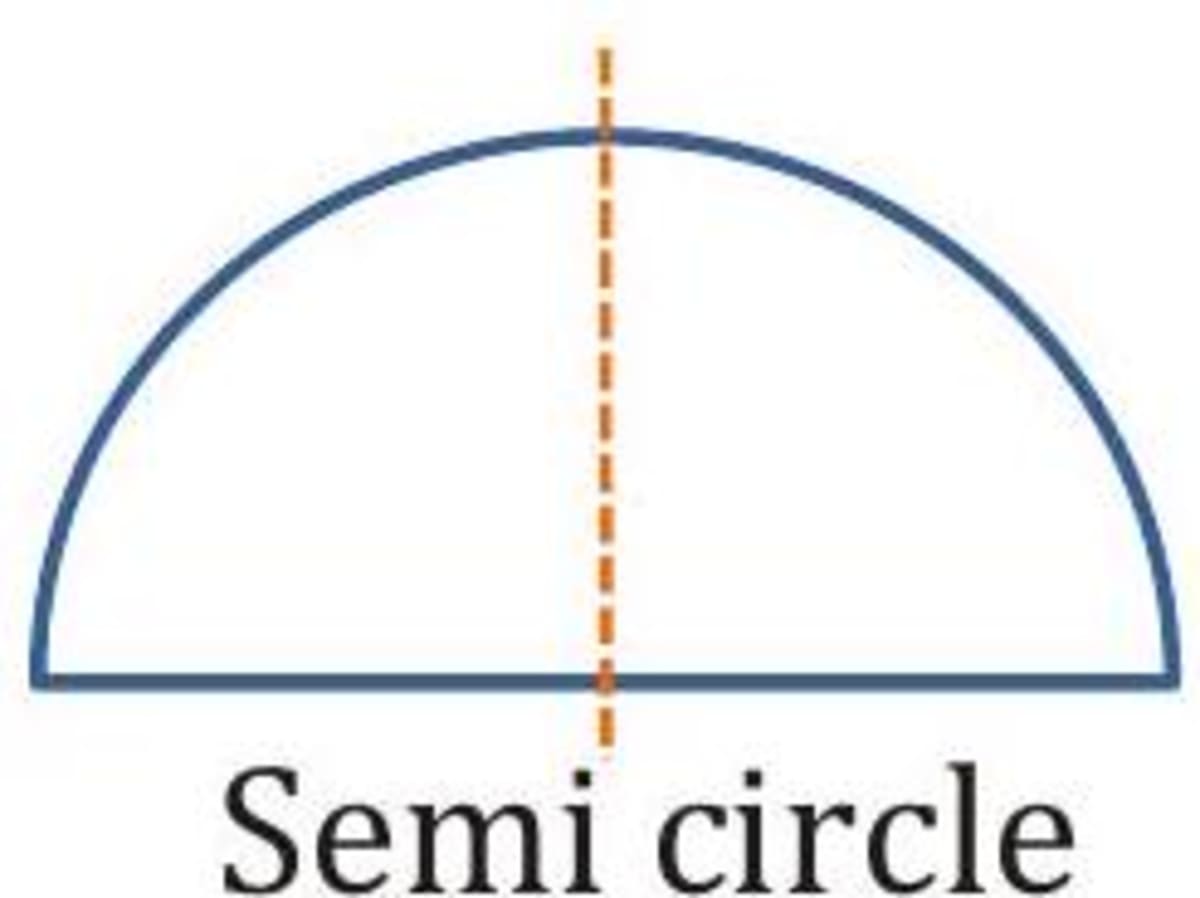
A semi-circle and a circle

(i) A semicircle has only 1 line of symmetry. It does not have any rotational symmetry.

7.0Numerical Ability

Q. Draw the lines of symmetry of the following figures.

• Explanation (i) MN - the angular bisector of $\angle \mathrm{RTS}$ (or $\angle \mathrm{PTQ}$ ) is the line of symmetry.
  
  (ii) There are two lines of symmetry i.e., $l$, m.
  
  (iii)
  
  (iv)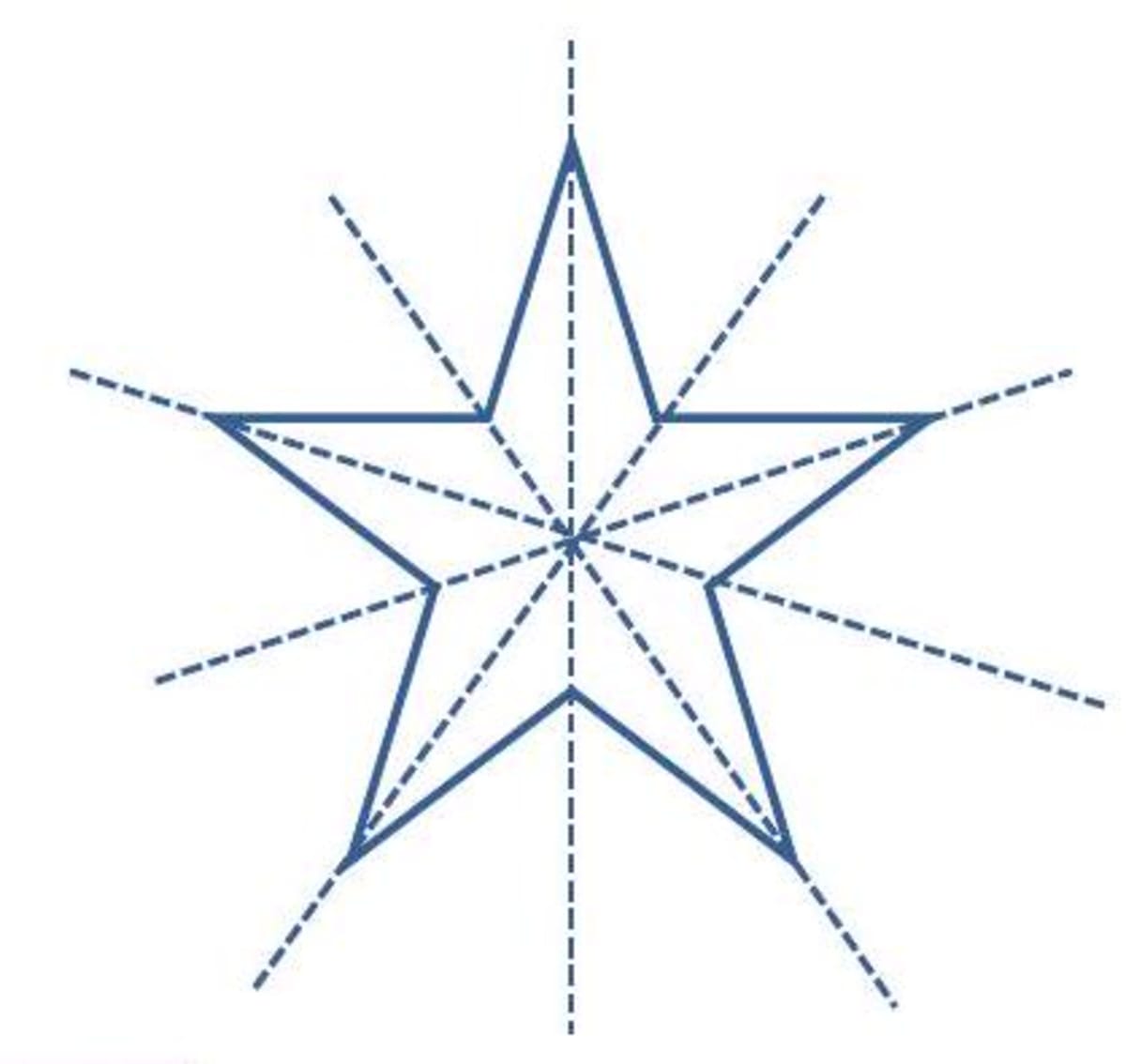
  

Q. Part of a geometrical figure is given in each of the diagrams given below. Complete the figures so that the dotted line in each case is a line of symmetry of the completed.

• Explanation
  
  (ii)
  
  (iii)
  
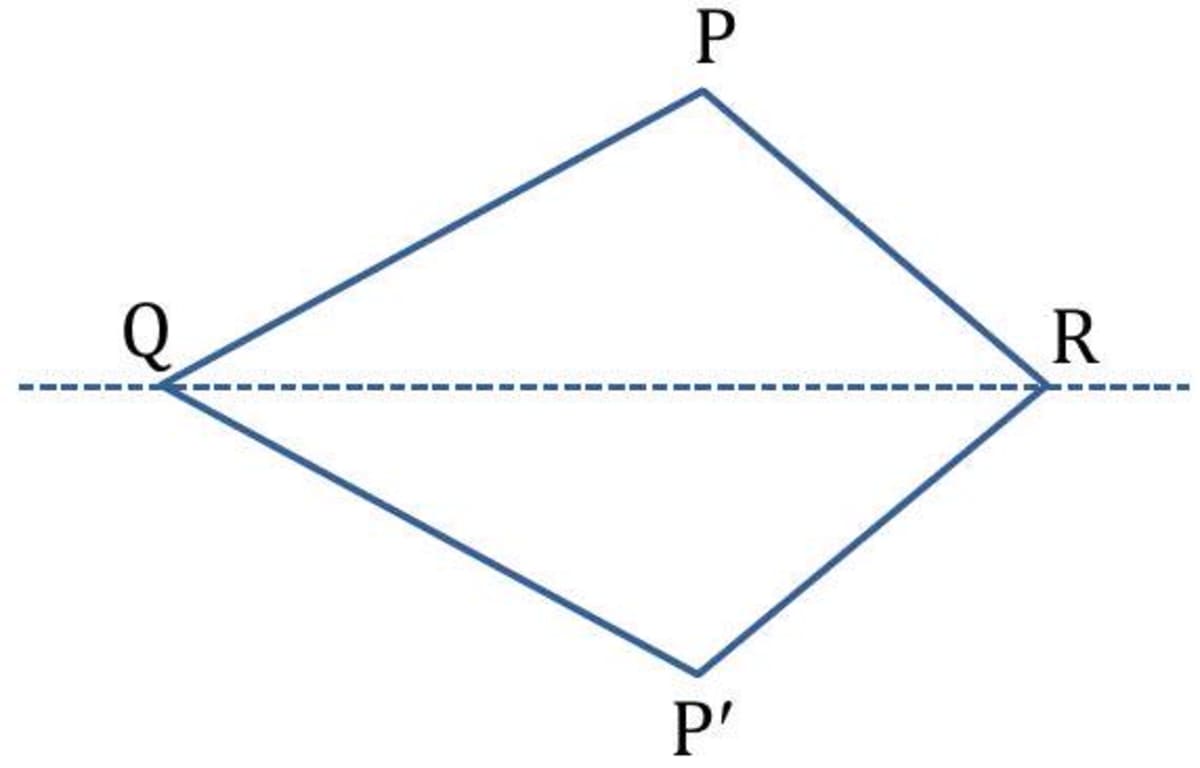  (iv)
  

Q. Copy the diagram and complete the shape to be symmetric about the mirror line.

• Explanation Step 1: Label the vertices. Draw straight line from A to cut the mirror line at $90^{\circ }$.
  
  Step 2: Measure the distance. Continue the line behind the mirror and measure the same distance and mark ${\mathrm{A}}^{\prime }$. Step 3: Repeat with the other vertices and join up the points.
  

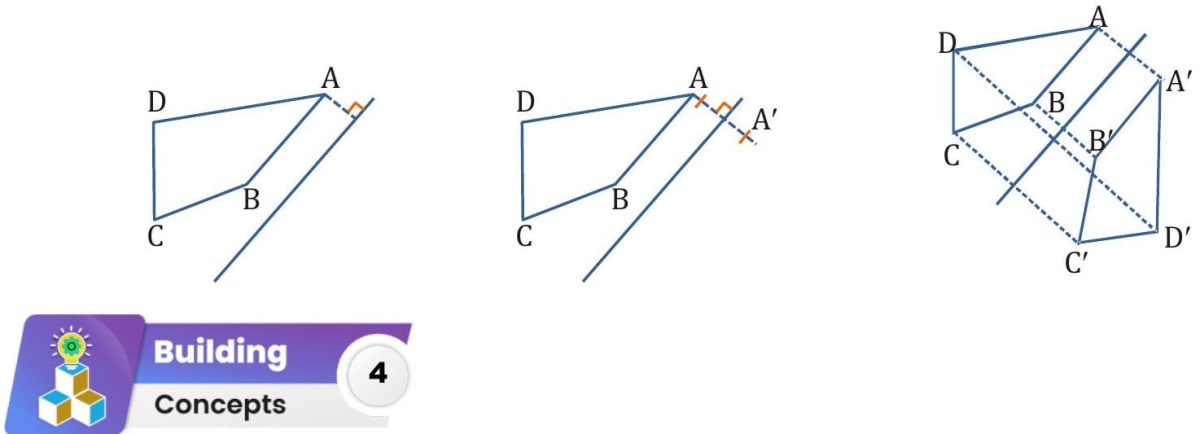
Q. Copy the diagram and complete each shape to be symmetric about the mirror line. (i)

• Explanation (i)
  
  (ii)
  

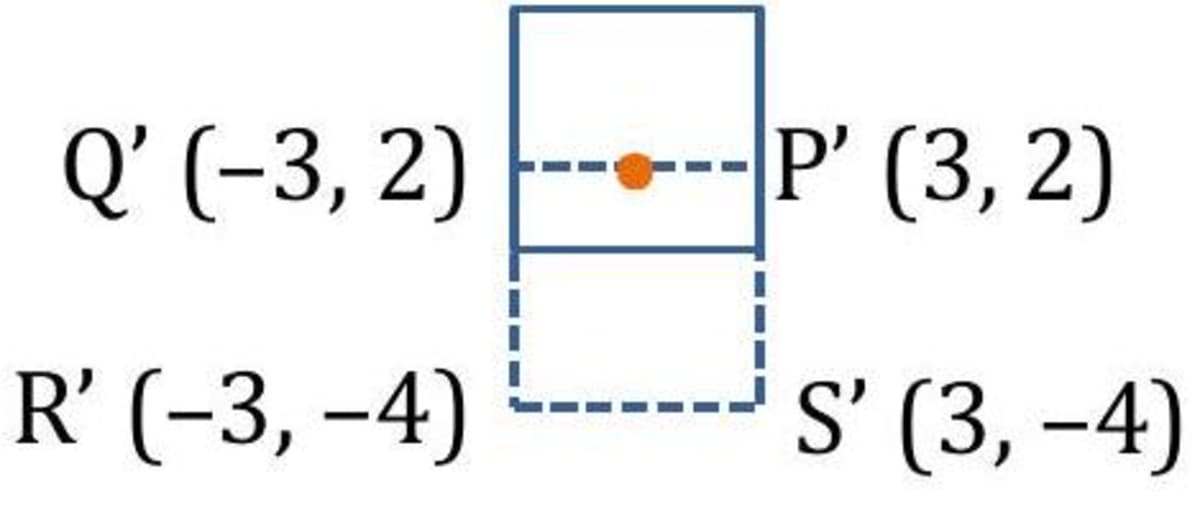
Q. A square $PQRS$ having its vertices at $P(-3,-2),Q(3,-2),R(3,4)$ and $S(-3,4)$ is shown below. It is rotated through $180^{\circ }$ about the origin 0 . Construct the new square $P^{\prime }{Q}^{\prime }{R}^{\prime }{S}^{\prime }$.

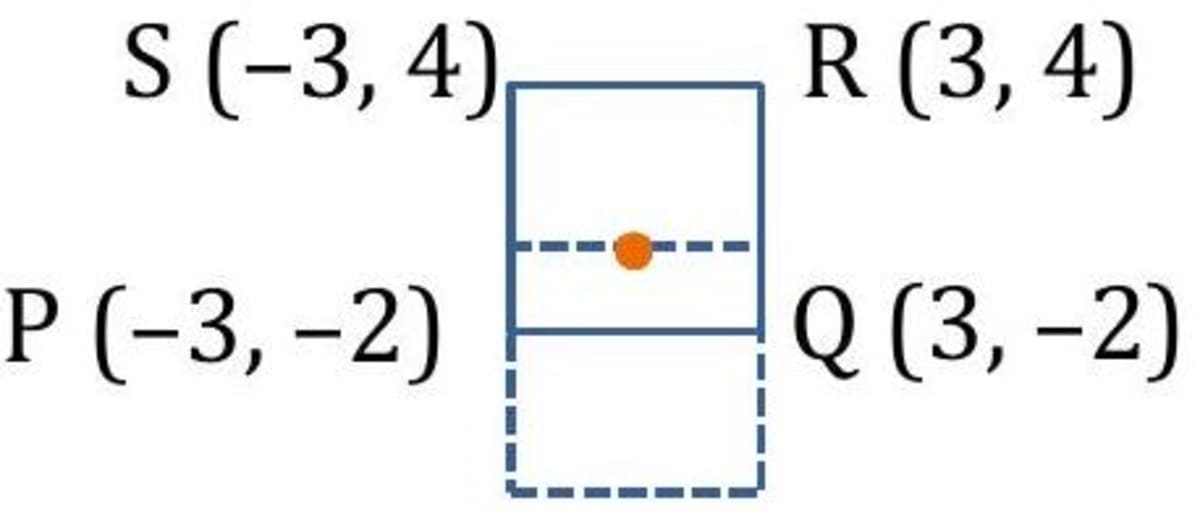
• Explanation:
  
  $P(x,y)$ takes the position $P^{\prime }(-x,-y)$ then, $P(-3,-2)\to P^{\prime }(3,2)$ $\mathrm{Q}(3,-2)\to {\mathrm{Q}}^{\prime }(-3,2)$ $\mathrm{R}(3,4)\to {\mathrm{R}}^{\prime }(-3,-4)$ $S(-3,4)\to S^{\prime }(3,-4)$

Q. Find out which of the following figures have rotational symmetry about the marked point and also find the order of rotational symmetry.

• Explanation (i) As shown here, the given figure fits onto itself after rotation through $180^{\circ }$. It will fit again onto itself after a further rotation of $180^{\circ }$. Thus, it fits onto itself twice during a rotation of $360^{\circ }$. Hence, it has a rotational symmetry of order 2.
  
  (ii) The given figure fits onto itself after a rotation through $90^{\circ },180^{\circ },270^{\circ }$ and $360^{\circ }$, i.e., it does so four times. So, it has a rotational symmetry of order 4.
  
  (iii) The given figure fits onto itself only once, i.e., when it is rotated through $360^{\circ }$. So, it does not have a rotational symmetry.
  
  (iv) The figure fits onto itself when rotated through $120^{\circ },240^{\circ }$ and $360^{\circ }$. So, it has rotational symmetry of order 3 .
  
  The lines $\ell ,m$, and $n$ are the three lines of symmetry.