Whole Numbers

Count the number of apples shown below.

When you count, you start counting from one, then go on to two, three, four, etc. This is the natural way of counting any set of objects. Hence, are called counting numbers or natural numbers. The number of students in a class, the number of days in a week are all examples of natural numbers. The natural numbers along with zero form the collection of whole numbers.
1.0Successor and Predecessor
Successor
The number which comes immediately after a particular number is called its successor. The successor of a whole number is the number obtained by adding 1 to it. Successor of a given number is 1 more than the given number. We observe that every whole number has its successor.
- Successor is obtained by adding 1 to given whole number.
- Predecessor is obtained by subtracting 1 from the given whole number.
- Number + 1 = Successor
Predecessor
The number which comes just before a particular number is called its predecessor. The predecessor of a whole number is one less than the given number. We observe that every whole number, other than zero, has its predecessor.
- Number-1 = Predecessor
Also, if is the successor of , then is the predecessor of .
- Whole number 0 has no predecessor.
2.0Number line
You can represent whole numbers on a number line. Draw a line. Mark a point on it. Label it 0 . Mark a second point to the right of 0 . Label it 1 . The distance between these points labelled as 0 and 1 is called unit distance. On this line, mark a point to the right of 1 and at unit distance from 1 and label it 2 . In this way go on labelling points at unit distances as ,... on the line. You can go to any whole number on the right in this manner. This is a number line for the whole numbers.

Addition on the number line
Addition of whole numbers can be shown on the number line. Let us see the addition of 3 and 4.

Subtraction on the number line
The subtraction of two whole numbers can also be shown on the number line. Let us find 7-5.

Multiplication on the number line
We now see the multiplication of whole numbers on the number line. Let us find .

Start from 0, move 3 units at a time to the right, make such 4 moves. Where do you reach? You will reach 12. So, we say, .
3.0Properties of whole numbers
Four basic operations - addition, subtraction, multiplication, and division can be performed on whole numbers. You will now learn about some properties of these operations.
Closure property
The difference and the quotient of two whole numbers is not always a whole number but the sum and product of two whole numbers is always a whole number. This is the closure property of the whole numbers. If and are two whole numbers, then (i) , then c is also a whole number.
For e.g., (whole number) (ii) , then c is not always a whole number.
For e.g., and (not a whole number). (iii) , then c is also a whole number.
For e.g., (whole number). (iv) is not always a whole number.
For e.g., (whole number) but (not a whole number). Hence, whole numbers are closed under addition and multiplication but are not closed under subtraction and division.
- While doing division and subtraction we can get decimals and negative number respectively. That's why division and subtraction is not closed under closure property.
Commutative property
The order in which we add or multiply two whole numbers does not alter the solution but is not true in case of subtraction and division. This is the Commutative property of the whole numbers. Let a and b are two whole numbers, then (i) . (ii) (iii) . (iv) Hence, only addition and multiplication are commutative for whole numbers.
Associative property
The sum and the product of three whole numbers do not change even if the grouping is changed but it is not true in the case of subtraction and division. This is the Associative property of the whole numbers. Let , and c are three whole numbers, then (i)
For e.g., (ii) .
For e.g., . (iii) .
For e.g., . (iv) .
Hence, addition and multiplication are associative for whole numbers.
Add the numbers 234, 197 and 103. Solution
Identity (for addition and multiplication)
What happens when you add zero to any whole number? You get the same whole number again. Hence, zero is called the additive identity of a whole number because it maintains the identity of the number during the operation of addition. Zero has a special role in multiplication too. Any whole number when multiplied by zero becomes zero.
Now, let's talk about multiplicative identity. Can you think of a whole number which when multiplied by any whole number gives that whole number itself as the answer. Yes, it is one. One is the multiplicative identity for whole numbers. Note: If zero is divided by a whole number, the result will always be zero.
Some important rules to learn.
- a+0=a
- a }\times0=
- a < 1=a
4.0Patterns in whole numbers
Numbers and elementary shapes can be correlated using patterns. Whole numbers can be arranged in different shapes as:
Every whole number (greater than 1) can be arranged as a line; • • • • • • • • •
- Some numbers can be arranged as squares.
These are also known as perfect squares.

- Some numbers can be arranged as rectangles.
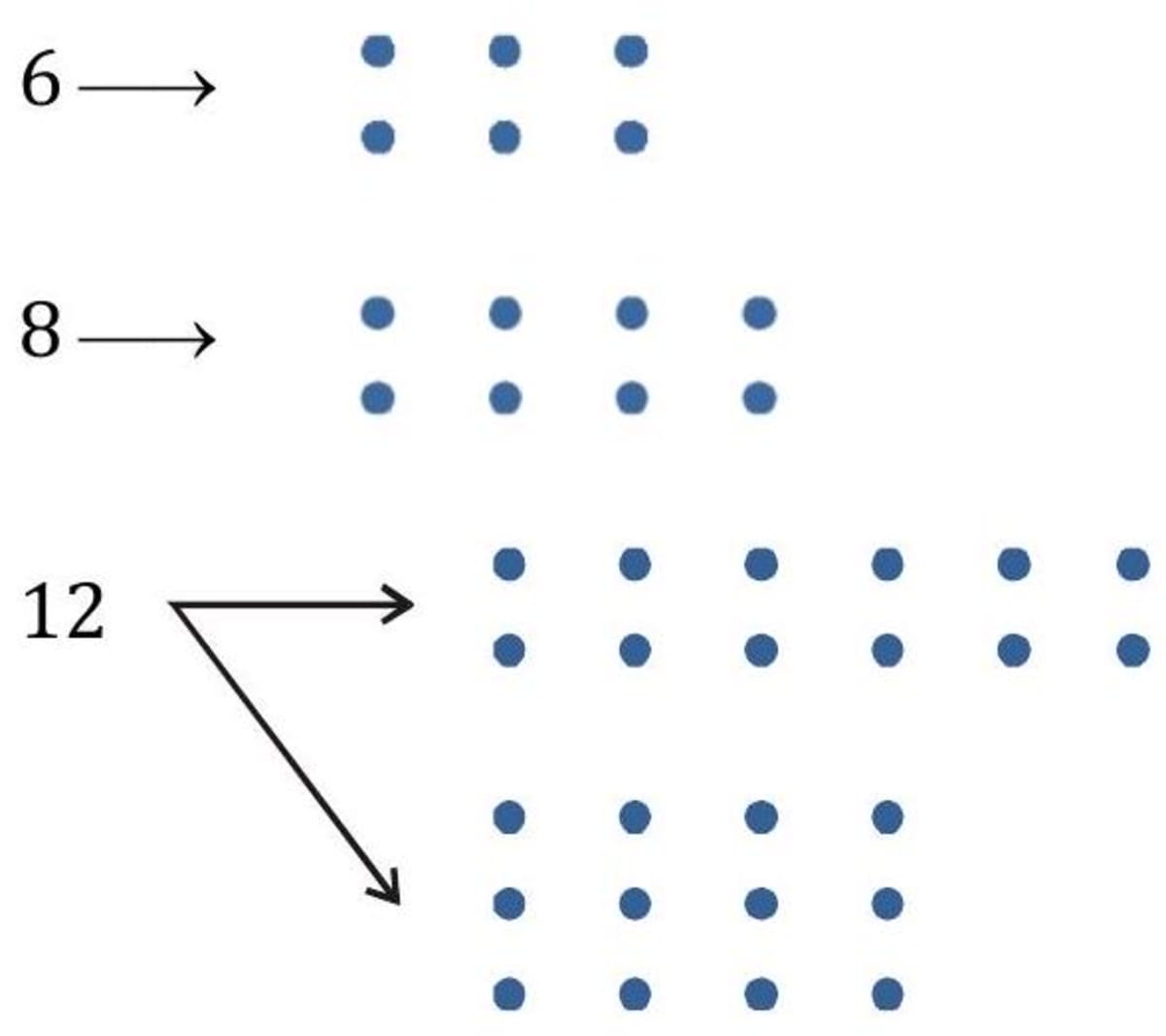
- Some numbers can be arranged as triangles.

5.0Pattern observations
The mathematical operations can be simplified by observing patterns.
- Pattern 1
- Pattern 2 and so on.
- Pattern 3
- Pattern 4
6.0Numerical Ability
How many whole numbers are there between 32 and 53 ?
- Explanation Whole numbers between 32 and That is
Find the successor and predecessor of 6199, 8540, 934, 13469.
- Explanation
(i) Write the next three natural numbers after 10999. (ii) Which is the smallest whole number?
- Solution Next three natural numbers after 10999 are (ii) Smallest whole number is 0 .
(i) Show addition of 4 and 5 on number line. (ii) Subtract 3 from 8 using number line.
- Explanation
(i) Addition of 4 and 5
(ii) Subtract 3 from 8


What is the value of in the given number line?
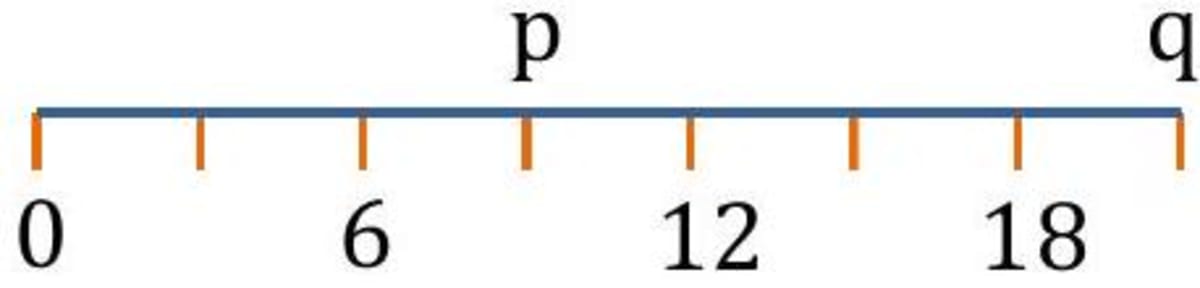
- Solution from the number line from the number line
Find .
- Solution In the above example, we have used associativity to get the advantage of multiplying the smallest even number by a multiple of 5 . Distributive property
A florist arranges 6 gladioli and 7 roses in a bouquet, Raj buys 5 such bouquets for the school annual function. What is the total number of flowers in these 5 bouquets?
- Explanation Gladioli in 5 bouquets flowers flowers Roses in 5 bouquets flowers flowers Total number of flowers in 5 bouquets flowers Another way of solving the problem is as follows. Flowers in one bouquet (gladioli + roses flowers Total number of flowers in 5 bouquets flowers flowers flowers So, Hence, we can conclude that if and c are whole numbers, then This property is called the distributive property of multiplication over addition.
There are 7 plates. Six biscuit are placed on each plate. If 4 biscuits are taken away from each plate, how many biscuits are left on the plates? Write the mathematical statement.
- Explanation Biscuits on 7 plates biscuits Biscuits taken away from 7 plates biscuits Biscuits remaining biscuits or, Biscuits left on one plate biscuits Biscuits left on 7 plates biscuits biscuits So, the mathematical statement So in above case, multiplication is distributive over subtraction also. But if is greater than , then ( ) does not exist in whole numbers. If and c are whole numbers, then if and only if is greater than .
7.0Memory Map

Related Article:-
Join ALLEN!
(Session 2026 - 27)