NEETClass 11thClass 12thClass 12th PlusJEEClass 11thClass 12thClass 12th PlusClass 6-10Class 6thClass 7thClass 8thClass 9thClass 10thOnline CoursesDistance LearningInternational OlympiadNEETClass 11thClass 12thClass 12th PlusJEE (Main+Advanced)Class 11thClass 12thClass 12th PlusJEE MainClass 11thClass 12thClass 12th PlusClass 6-10Class 6thClass 7thClass 8thClass 9thClass 10thNEET2025202420232022JEE20262025202420232022Class 6-10JEE MainPrevious Year PapersSample PapersMock TestResultAnalysisSyllabusExam DatePercentile PredictorAnswer KeyCounsellingEligibilityExam PatternJEE MathsJEE ChemistryJEE PhysicsJEE AdvancedPrevious Year PapersSample PapersMock TestResultAnalysisSyllabusExam DateAnswer KeyEligibilityExam PatternRank PredictorNEETPrevious Year PapersSample PapersMock TestResultAnalysisSyllabusExam DateCollege PredictorAnswer KeyRank PredictorCounsellingEligibilityExam PatternBiologyNCERT SolutionsClass 6Class 7Class 8Class 9Class 10Class 11Class 12TextbooksCBSEClass 12Class 11Class 10Class 9Class 8Class 7Class 6SubjectsSyllabusNotesSample PapersQuestion PapersICSEClass 10Class 9Class 8Class 7Class 6State BoardBiharKarnatakaMadhya PradeshMaharashtraTamilnaduWest BengalUttar PradeshOlympiadMathsScienceEnglishSocial ScienceNSOIMONMTCASATInstant Online ScholarshipAIOT(NEET)TALLENTEXALLEN for SchoolsAbout ALLENBlogsNewsCareersRequest a call backBook a demo
Motion and Time
"The motion of this racing car, and of other moving objects, can be described in terms of the distance covered during a certain time period."
1.0Introduction
Motion is one of the more common events in your surroundings. You can see motion in natural events such as clouds moving, rain and snow falling, and streams of water moving, etc. Motion can also be seen in the activities of people who walk, jog, or drive various vehicles from place to place. Motion is so common that you may think that everyone understand the concepts of motion. The study of motion is called 'mechanics'. It is broken down into two parts, kinematics and dynamics. Kinematics is the "how" of motion, that is, the study of how objects move, without concerning that why they move. Dynamics is the "why" of motion. In dynamics, we are concerned with the causes of motion, which is the study of forces.
2.0Position and reference point
Suppose you live in near Allen Career Institute, Kota. Figure shows the aerial view (top view) of your locality. To reach Allen's building, you follow a path shown in the figure. Your house is the starting place for you to find the location, or position, of Allen's building.
A reference point is needed in order to describe the location of an object. point is also called the origin. To describe an object's position, three things must be included in the description : (i) a reference point, (ii) a direction from the reference point, (iii) distance from the reference point (the length of the line segment joining the reference point and the object).
For example, in figure, choose your house as the reference point. Next, choose a direction from the reference point, let it be 'towards the ABC garden' (see figure). Finally, give the distance from the reference point: let it be 1.2 km .
How to describe the reference direction?
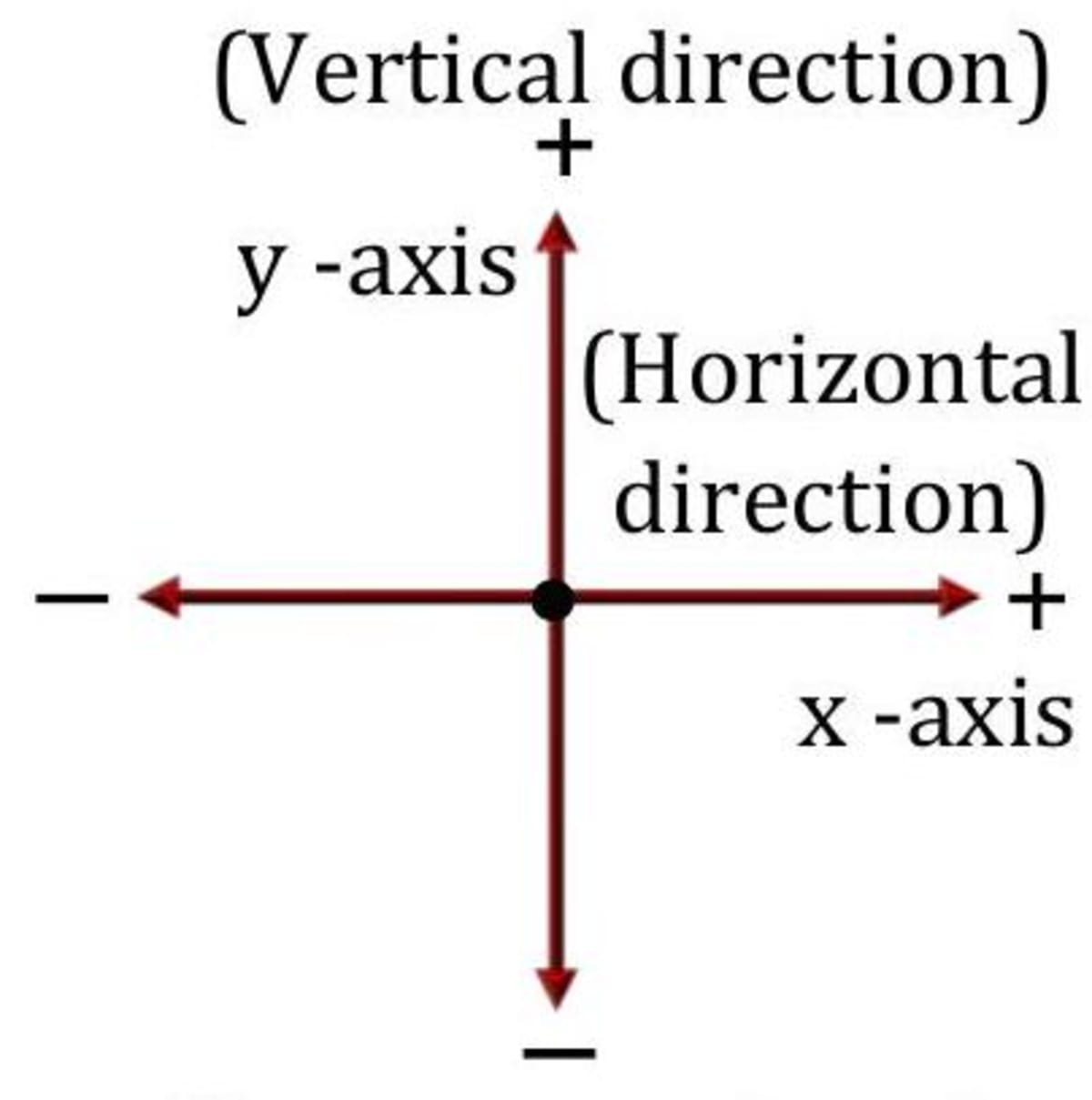
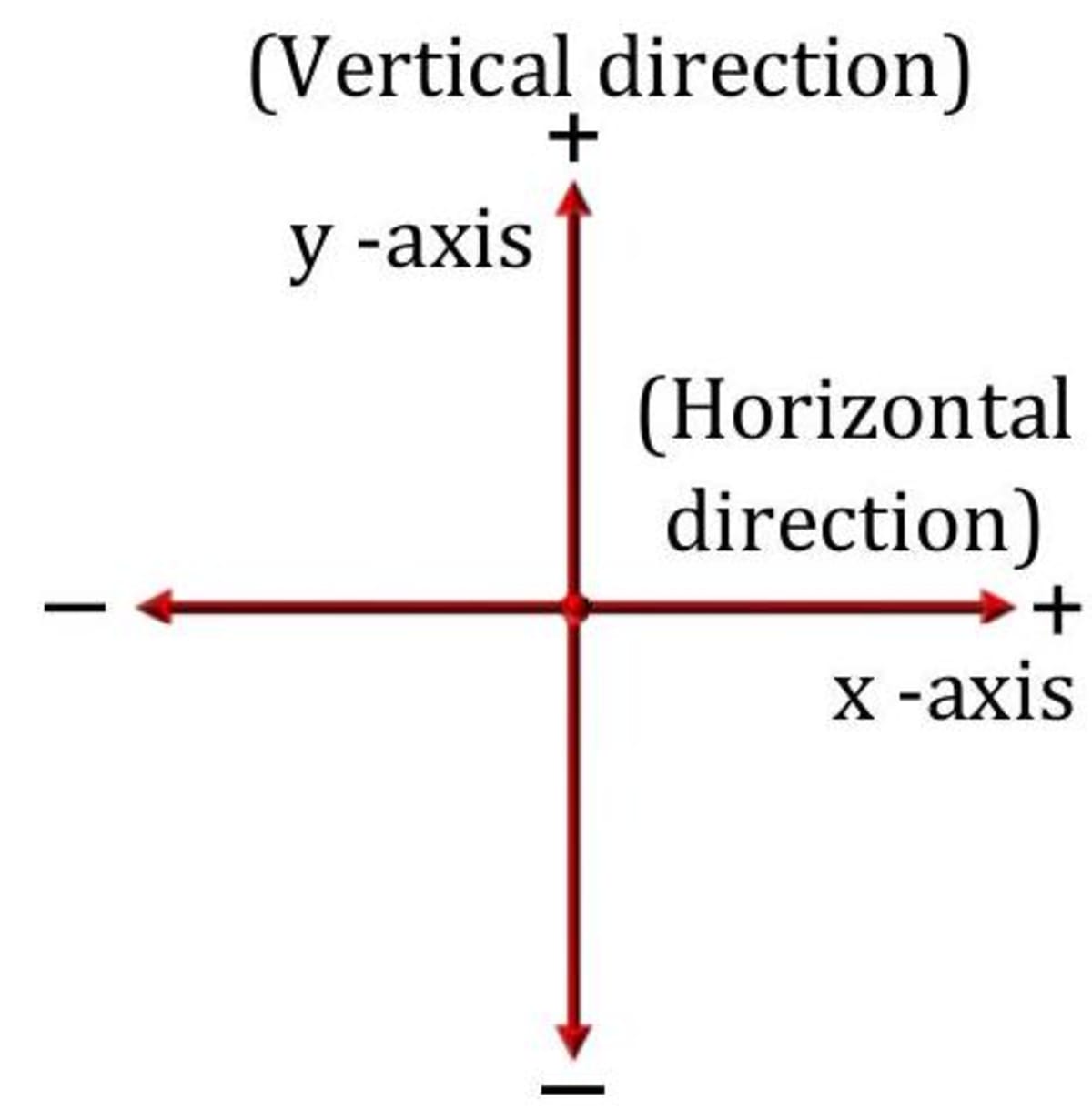
One way of indicating the direction is to use a plus ( + ) or a minus (-) sign. The plus sign can be the direction from the reference point, is in the reference direction (see figure). A minus sign means the direction is opposite to the reference direction. For example, plus ( + ) sign can be used to indicate 'towards the school' in the figure on previous page and minus (-) sign to indicate 'away from the school'.
The position of an object can be described as a distance from the origin together with a plus or minus sign that indicates the direction.
3.0Understanding motion
Consider a ball that you notice one morning in the middle of a lawn. Later in the afternoon, you notice that the ball is at the edge of the lawn, against a fence, and you wonder if the wind or some person moved the ball. You do not know if the wind blew it at a steady rate, or even if some children kicked it all over the yard. All you know for sure is that the ball has been moved because it is in a different position after some time passed. These are the two important aspects of motion: (1) A change of position (2) The passage of time
Moving involves a change of position during some time period. Motion is the act or process of something changing position. The motion of an object is usually described with respect to a stationary object. Such a stationary object is said to be 'at rest'.
- Motion is a change in an object's position with respect to time compared to a fixed object. If you ride in a car, your position changes compared to a tree or an electric pole.
- An object is said to be at rest if it does not change its position with time.
Rest and motion are relative terms
Imagine that you are traveling in an automobile with another person. You know that you are moving across the land outside the car since your location on the highway changes from one moment to another. Observing your fellow passenger shows that there is no change of position. You are in motion relative to the ground but you are not in motion relative to your fellow passenger. The motion of any object or body is the process of a change in position 'relative' to some reference object or location.
4.0Uniform and Non-Uniform motion
Uniform motion
If a body covers equal distances in equal intervals of time in a particular direction, its motion is called 'uniform motion'.
- A uniform motion always takes place in straight line. Any motion along a curved path is not a uniform motion. Examples : (i) A car moving with a constant speed in straight line. (ii) Motion of an athlete along straight path with constant speed.
In real world, we are rarely in uniform motion. We can be in uniform motion for a short time period but whenever we have to take turn, reduce speed or increase speed according to our need, we are not in uniform motion.
Motion of this cyclist is uniform motion, she is covering equal distances in equal intervals of time, she is moving in straight line in a particular direction.
Non-uniform motion
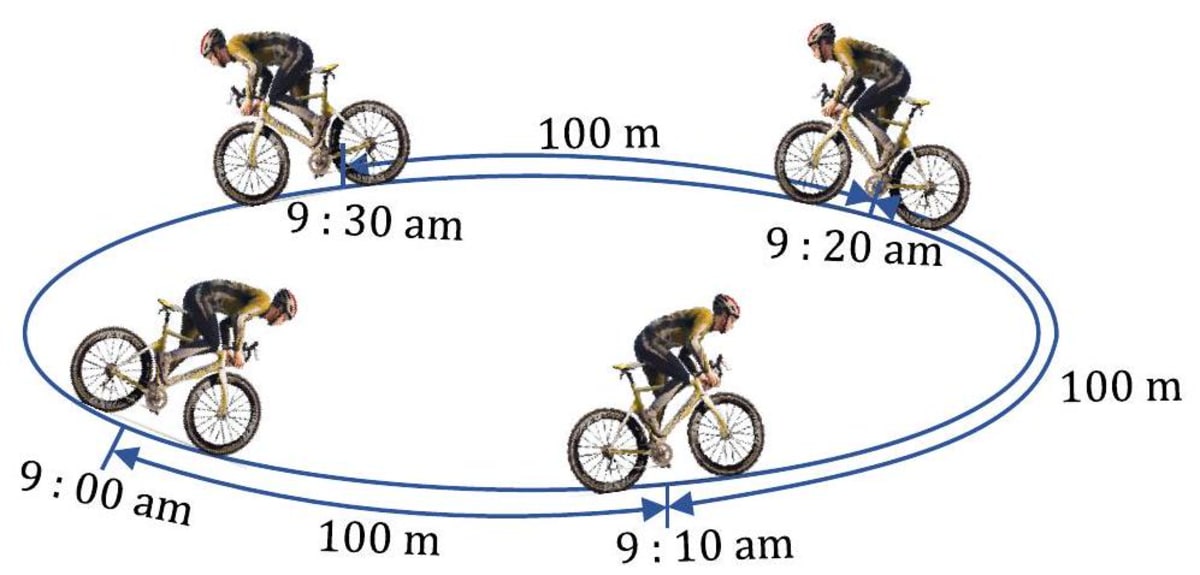
If a body covers unequal distances in equal intervals of time, its motion is called 'non-uniform motion'. Even if a body covers equal distances in equal intervals of time but it changes its direction, still its motion is said to be 'non-uniform'.
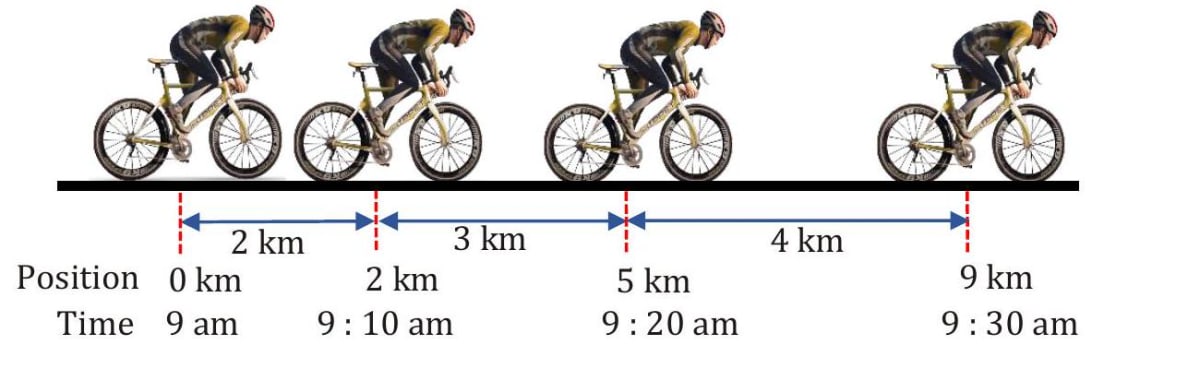
Motion of this cyclist is 'non-uniform', she is covering unequal distances in equal intervals of time, she is moving in straight line in a particular direction.
5.0Distance and displacement
Distance
The length of the actual path between initial and final positions of a moving object is called 'distance'.
6.0Important points related to distance
(1) Distance is a scalar quantity. (2) Distance depends on the path. (3) Distance is always taken positive
Unit of distance : In S.I. system, unit of distance is metre ( m ). Some other popular units are millimetre ( mm ), centimetre ( cm ), kilometre ( km ).
- Distance travelled by a vehicle is measured by a device called 'odometer'.
Displacement
The shortest distance between the initial position and the final position of the particle is called displacement. It is also defined as the change in the position of the particle.
Displacement =
Where, final position initial position.
Important points related to displacement:
- Displacement is a vector quantity, its direction is always taken from initial position to final position.
Sign conventions for displacement
- Displacement depends only on initial position and final position, but does not depend on path.
- Displacement of a particle in motion can be positive, negative or even zero.
Unit of displacement :
Units of distance and displacement are same as both represent some length. Thus, in S.I. system, unit of displacement is metre ( m ). Some other popular units are millimetre ( mm ), centimetre ( cm ), kilometre ( km ). Let us understand the distance and displacement using some real life situations. Suppose an athlete is running on a circular path. Let in a certain time interval, he moves from position A to position B as shown in figure. The distance travelled by the athlete is the arc length APB , while the displacement of the athlete is line segment .
Distance is always greater than or equal to the magnitude of displacement. Distance is exactly equal to displacement (i) when it follows a straight path without changing its direction (ii) when it is in uniform motion.
Note:
- Always take care of the direction (north, south, east, west) given in the problem.
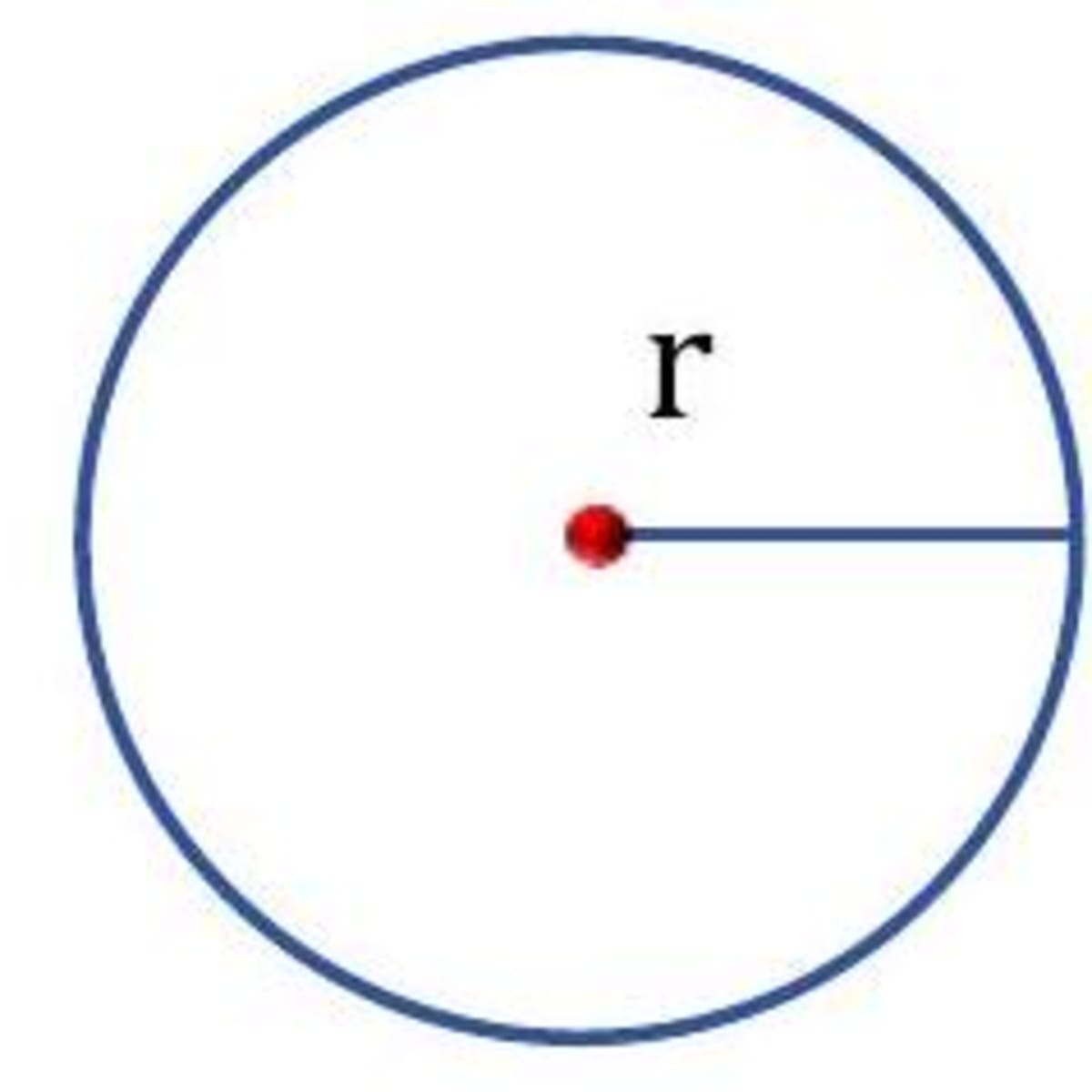
- For a Circle : Diameter Circumference or or 3.14
- For a rectangle and a square
Perimeter of rectangle Perimeter of square side
- A positive direction or a negative direction (opposite direction)
For e.g.,
(i) 5 m denotes a direction 5 m to the right. (ii) -5 m denotes a direction 5 m to the left.
- Position above or below sea level
For e.g.,
(i) Sea level is taken as 0 m .
(ii) The helicopter flies 350 m above sea level or +350 m .
(iii) The submarine lies 150 m below sea level or -150 m .
Whenever a particle changes its direction, distance is greater than displacement. Example: The bend in the road means that the distance the cyclists cover is greater than their final displacement.
- A body moving in a circular path when reaches its original position after one round, then the displacement at the end of one round is zero, but the distance travelled by it is equal to the circumference of circular path.
7.0Speed and velocity
Speed
The distance travelled by a particle per unit time is called speed.
Important points related to speed
- Speed is a scalar quantity.
- Speed depends on the path.
- Speed gives no idea about the direction of motion of the object.
- Speed can never be negative. In motion, it is taken positive ; at rest, it is zero.
In uniform motion, speed is always equal to the magnitude of velocity. In nonuniform motion, speed can only be either greater than or equal to the magnitude of velocity.
Unit of speed : S.I. system - metre/second (m/s). C.G.S.system - centimetre/second (cm/s).
Another commonly used unit for measuring speed is kilometer per hour. Now,
or,
Uniform speed :
An object is said to be moving with a uniform speed, if it covers equal distances in equal intervals of time. That is, magnitude of speed is constant.
Non-uniform speed :
An object is said to be moving with a variable speed, if it covers unequal distances in equal intervals of time. That is, magnitude of speed is variable.
Speedometer of the vehicle measures its speed (see figure).
Velocity
The rate of change of displacement is called velocity.
Important points related to velocity
- Velocity is a vector quantity.
- Velocity can be negative, positive or zero.
- Velocity does not depend on the path, it depends only on the initial position and final position of an object.
- Velocity gives the direction of motion of an object.
Unit of velocity : S.I. system - metre/second (m/s) C.G.S. system - centimetre/second (cm/s)
Uniform velocity :
A particle is said to have uniform velocity, if the magnitude as well as the direction of its velocity remains constant. It is possible only when the particle moves in straight line without changing its direction.
Non-uniform velocity :
A particle is said to have non-uniform velocity, if either the magnitude or direction of its velocity changes (or both changes).
Always take care of the units of the quantities like distance, time and speed given in the question. All the quantities should be in the same system of units.
Example : If the distance travelled by a body is 20 m , in 2 min , then find the speed of the body. Here, the time is to be converted into seconds, so that all the quantities are in same system of units and the final answer is also in the correct units.
8.0Measurement of time
We tell time many times a day. When is football practice? What time is the dinner? When does the party start? We use clocks to tell time. They help people to plan their day.
If you did not have a clock, how would you decide what time of the day it is? Have you ever wondered how our elders could tell the approximate time of the day by just looking at shadows? How do we measure time interval of a month? A year?
Our ancestors noticed that many events in nature repeat themselves after definite intervals of time. For example, they found that the sun rises everyday in the morning. The time between one sunrise and the next was called a day. Similarly, a month was measured from one new moon to the next. A year was fixed as the time taken by the earth to complete one revolution of the sun.
History of measuring time
People have been telling time for a long, long time. Clocks from long ago did not look like ours and they did not keep the best time either.
Once upon a time, people woke up when the sun rose and went to bed when the moon and stars came out. These were the first clocks.
Starting in 1400 BC, ancient Egyptians and Greeks used water clocks to tell time during the day and the night. Water was poured into a bowl with holes in it. As the water dripped out through the holes, people checked the water levels using special marks. This told them how much time had passed.
Some of the instruments made by the man in the earlier times are Sun dial, Sand clock, Candle clock. In 1582 , Galileo Galilei noticed that an oil lamp swinging from a chain kept perfect time. He found that a swinging weight always took the same time to go backward and forward. Another name for a swinging weight is a pendulum. In 1657, Christian Huygens invented a clock that used a pendulum to keep time. Sailors used hourglasses filled with sand or powdered eggshells to tell time. The powder would take one hour to flow from the top bulb to the bottom bulb.
Greenwich Mean Time (GMT) :
It is the time in Greenwich, England. Each time zone was described by how many hours away from GMT it was. In the 1880s, women were the first to wear wristwatches. After soldiers wore them in World War I, men liked to wear them as well.
Later, watches with tiny quartz crystals inside became the best timekeepers. The crystals moved like pendulums, but kept even better time. Quartz watches are still popular today.
In 1972, quartz watches went digital. A display of numbers appeared instead of a clock face.
Simple pendulum
The working of clocks is rather complex. But all of them make use of some periodic motion. One of the most well-known periodic motions is that of a simple pendulum.
- A simple pendulum consists of a small metallic ball or a piece of stone suspended from a rigid stand by a thread [see figure(a)]. The metallic ball is called the bob of the pendulum. Figure (a) shows the pendulum at rest in its mean position. When the bob of the pendulum is released after taking it slightly to one side, it begins to move to and fro [see figure (b)]. The to and fro motion of a simple pendulum is an example of a periodic or an oscillatory motion.
Oscillatory motion of a pendulum The pendulum is said to have completed one oscillation when its bob, starting from its mean position 0 , moves to A , to B and back to 0 . The pendulum also completes one oscillation when its bob moves from one extreme position to the other extreme position and comes back to A.
The time taken by the pendulum to complete one oscillation is called its time period. Time period
Unit of time : The S.I. unit of time is second (s). Some commonly used units of time are minute and hour.
1 minute hour minutes ; 1 hour
9.0Graphical representation of motion
Graph
A graph is a line, straight or curved, showing the relation between two variable quantities, of which one varies as a result of the change in the other.
Distance/displacement-time graph
This graph is plotted between the time taken and the distance covered, the time is taken along the x -axis and the distance covered is taken along the y -axis.
When the body is at rest
When position of the body does not change with time then it is said to be stationary. The distance-time graph of such a body is a straight line parallel to x -axis.
When the body is in uniform motion
In uniform motion, constant as speed Now, Since is constant , thus, the distance-time graph of such a body is a straight line, inclined to x -axis.
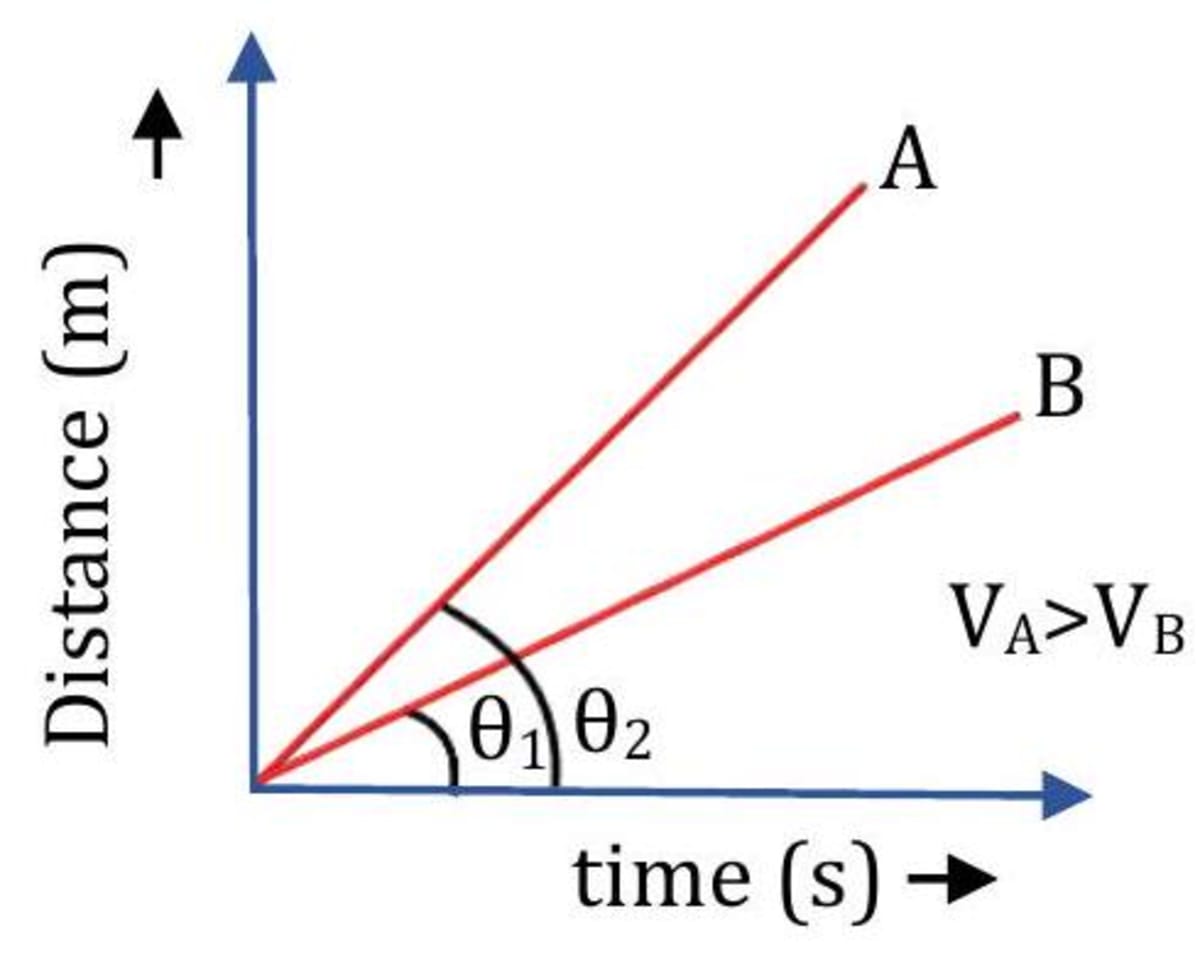
Slope Slope Thus, slope of distance-time graph gives speed of the body (see figure).
In a distance-time graph, more the slope of the graph of an object in motion, more will be its speed and vice-versa. Example : In given graph (figure) speed of particle A is greater than the speed of particle because slope of graph of particle is greater than slope of graph of particle B.
- In distance time graph where body is in a straight line parallel to x -axis. Speed is zero.
- The slope of distance/displacement time graph gives the speed/velocity of the body.
- More the slope of distance/displacement time graph more will be the speed/velocity of the moving body.
10.0Concept Map
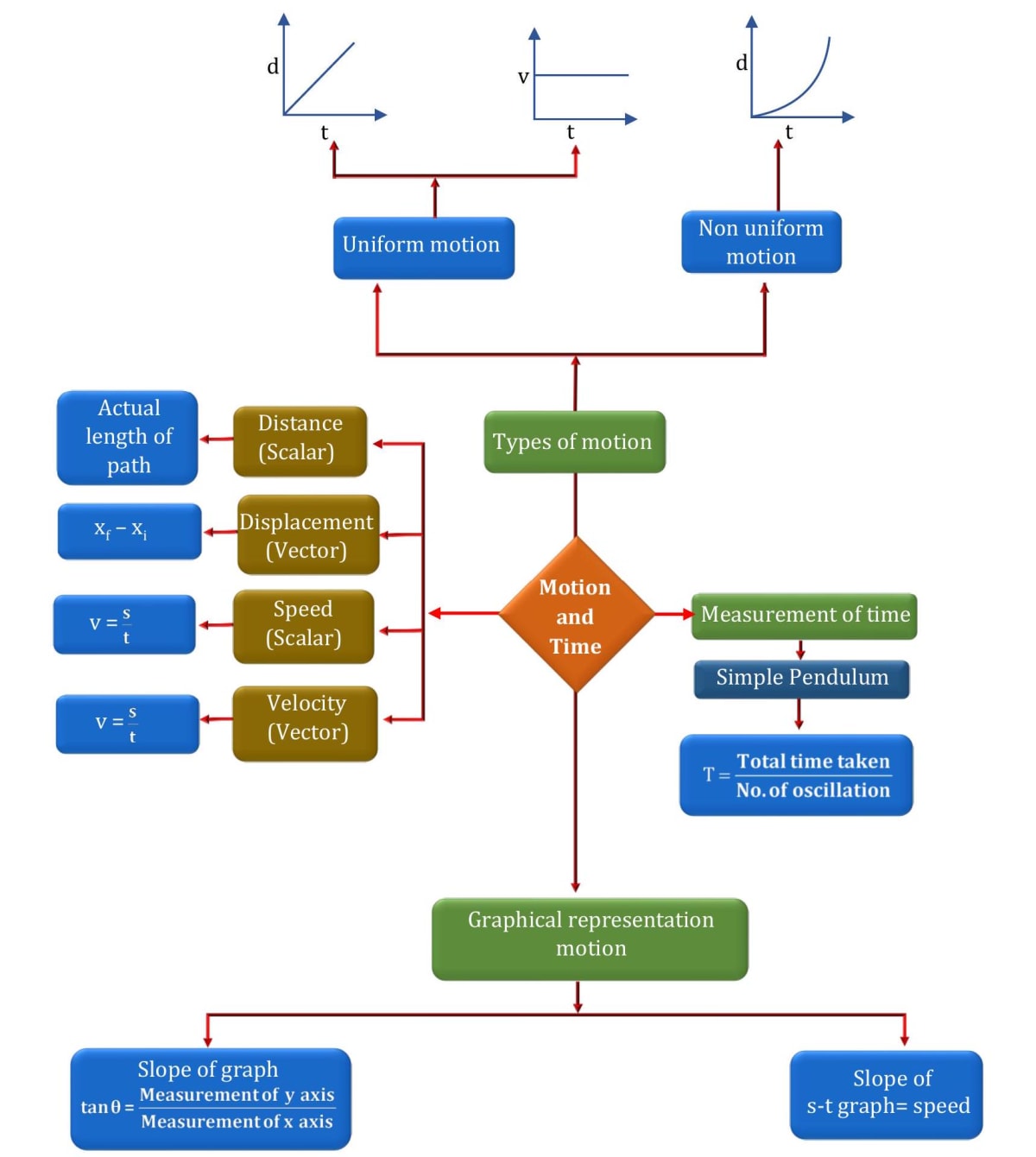
Important units, formulae, and quantity
11.0Numerical Ability
In figure, a squirrel runs on the ground from the 20 cm mark (its initial position) to the 100 cm mark. After that, it reverses and runs to the 50 cm mark (its final position). Find the displacement and distance travelled by the squirrel.
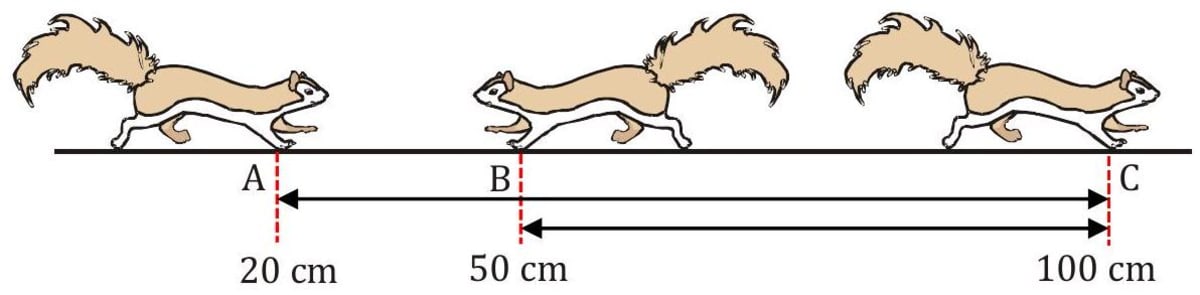
- Solution: To find the displacement, we should know the initial and the final position of the particle. Apply the formula: Displacement Distance Length of actual path travelled Given, initial position, ; final position, Displacement Now, distance travelled by squirrel from A to C, Distance travelled by squirrel from to Total distance travelled by squirrel Whenever a particle changes its direction or follows a curved path, distance is always greater than the magnitude of displacement.
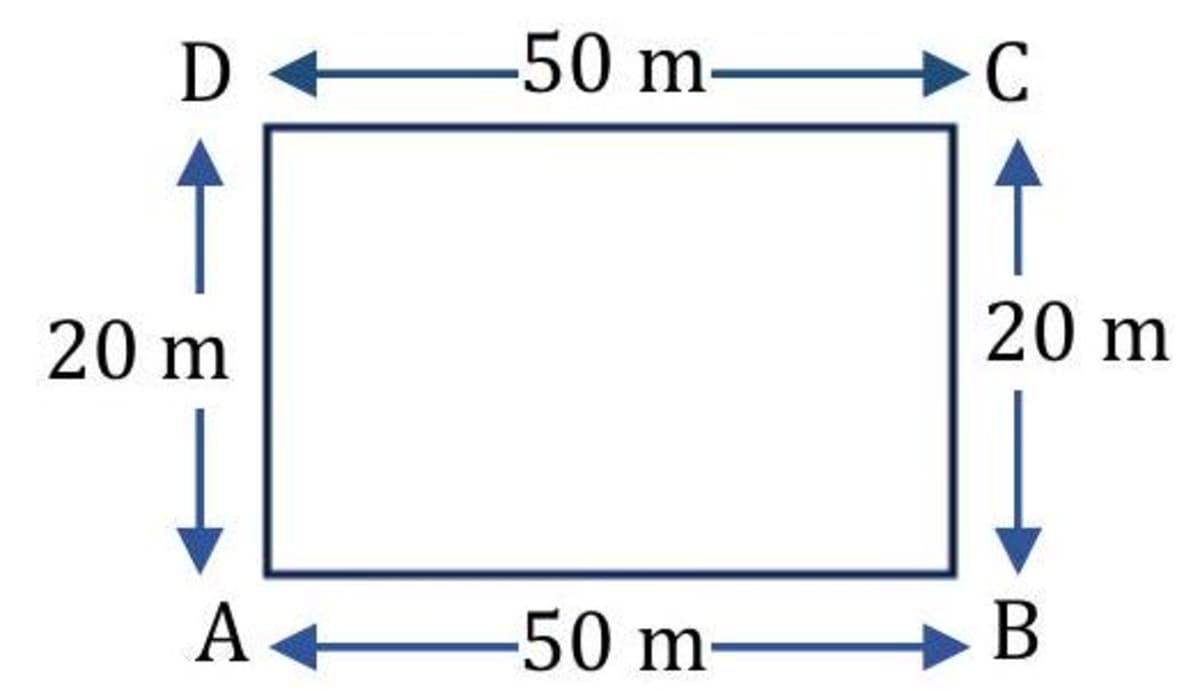
A playful dog runs along the path shown in figure, starting at A and following through all arrows. The distance from to is , and the distance from to is . The total time the dog takes to go from along the path and back to again is 16s. What is the dog's distance and displacement covered for the entire trip?
- Solution: Decode the problem To find the distance, we apply the formula of perimeter of the rectangle. Apply the formula 2 ( ) Given, the dog runs along a rectangular path. Length of rectangle, , breadth of rectangle, Distance covered by the dog Perimeter of rectangle Displacement , as the final point is same as the initial point.
A car moves on a circular path of radius . Find the distance travelled by the car when it moves from position to position and displacement as shown in figure below.
- Solution: To find the displacement or distance in of a circle we must know circumference of the circle. Apply the formula value of or In the given figure the distance travelled is half of the circumference of the circle i.e., Distance Since initial position of car is A and its final position is B, thus, displacement of the car is AB. Here, displacement is equal to the diameter of the circle. As we know that the diameter of a circle is twice the radius of the circle, thus, Displacement, .
A bus travels 54 km in 90 minutes. What is the speed of the bus in and .
- Solution Decode the problem: First convert all the quantities in same system of units Apply the formula Speed Given, Distance ; Time minutes Speed
Calculate the speed of a swimmer who swims in s.
- Solution: Given, distance ; time, Speed
A passenger train travels from Kota to New Delhi, a distance of 350 km, in . Find the train's speed in (i) (ii) m/s.
- Solution: (i) Given, distance ; time, (ii) Speed
An object is moving along a curved path of radius 7 m . It reaches from to figure in 10 s . Find the speed and velocity of the object. Take, .
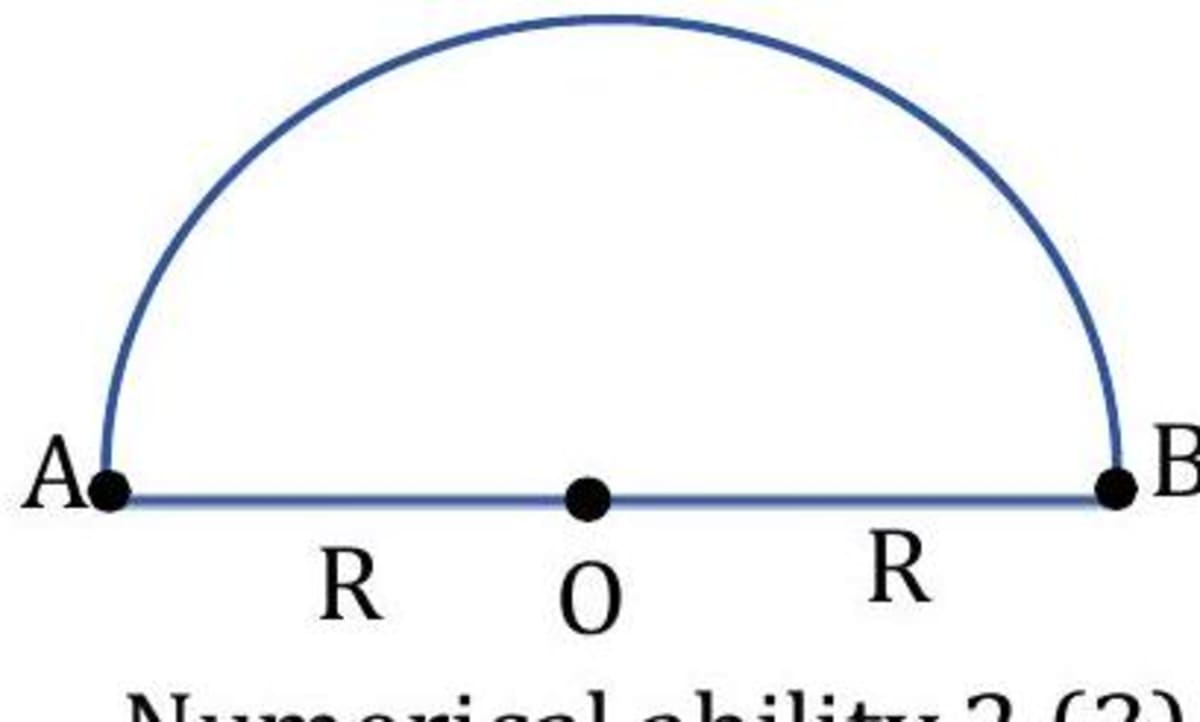
- Solution Given, radius, ; time, . Here, distance covered by the object in moving from to is half of the circumference of the circle i.e., Distance Speed Here, displacement is equal to the diameter of the circle i.e., Displacement Velocity
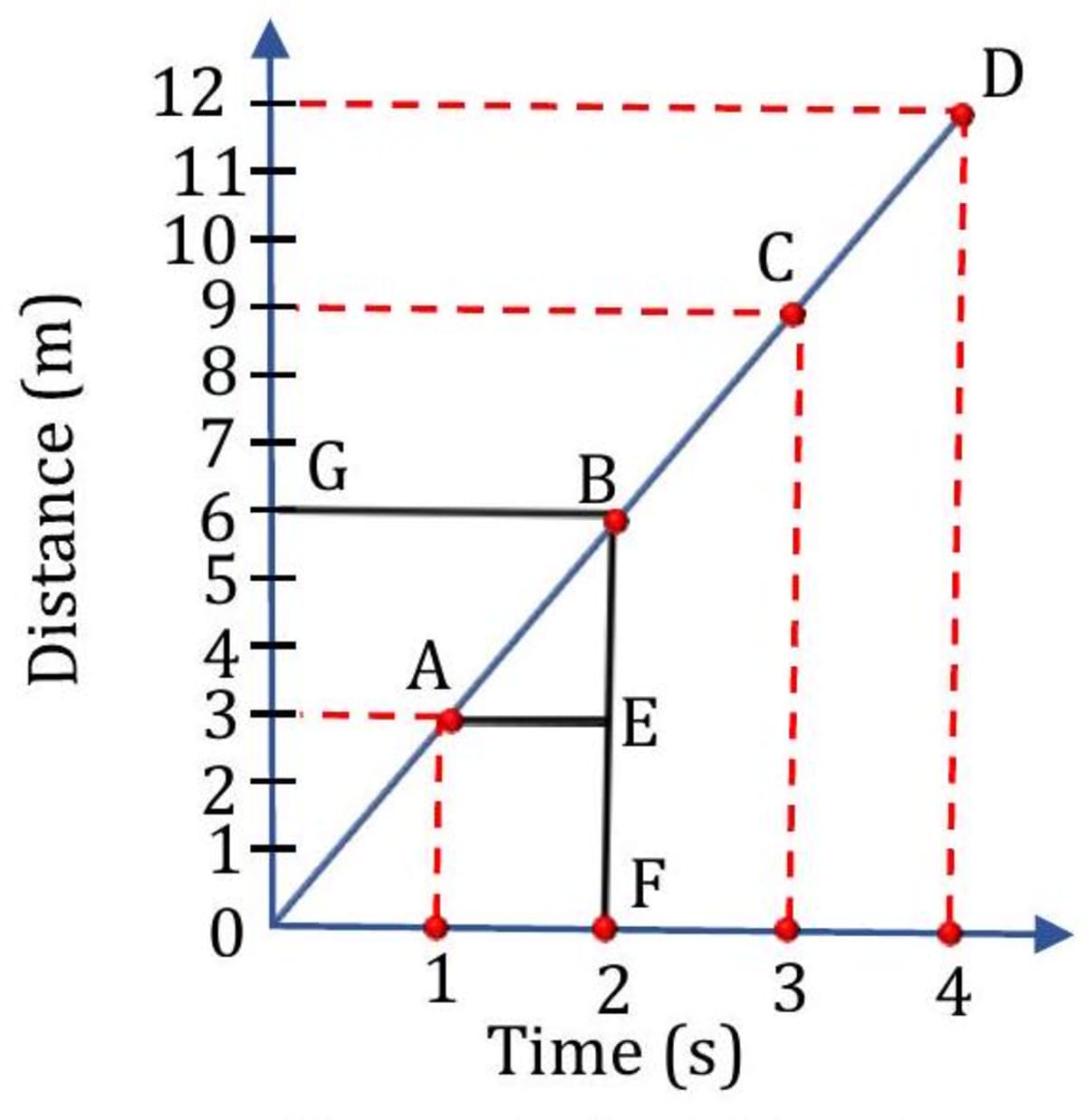
The distance covered by moving body was recorded after every 1 s for 4 s . The data is given in the table below. Represent it graphically and find the speed of the body from the graph.
- Solution
The body covers equal distance in equal interval of time. The distance-time graph of a body in uniform motion is a straight line. The horizontal axis represents time, while the vertical axis represents distance.
Speed Slope
If we study the graph carefully, we will see that would also give the speed of the body. BE gives the distance travelled in the time interval AE , which is 1 s .
Car's odometer reads at the start of trip and 10720 km at the end. Determine the distance travelled by car.
- Solution Distance
In the given figure a rabbit moves from place 'A' to place ' B ' and reaches place ' C '. How much distance the rabbit covers from place A' to place 'C?
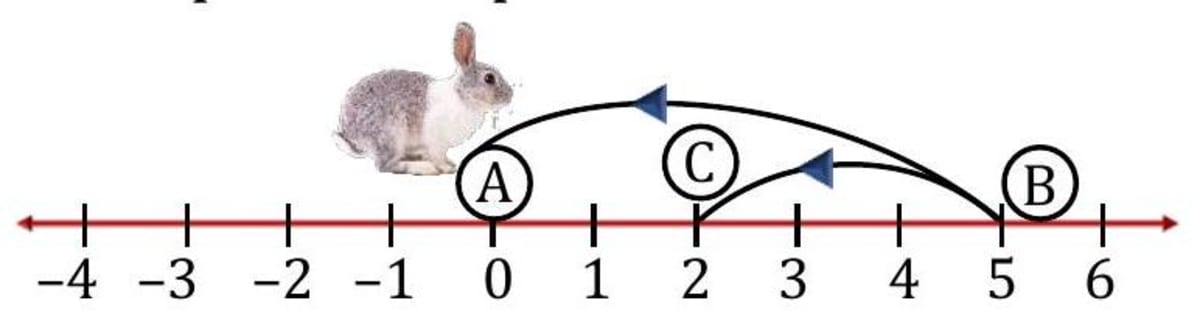
- Solution When rabbit moves from A to B the total distance covered is 5 units When the rabbit moves from to , the distance it covers is units. Total distance covered units +3 units units.
A runner travels around rectangle track with length 50 m and width 20 m . After travels around rectangular track he return back to starting point. How much distance he travelled?
- Solution
Suppose runner started from point A and by passing through point reached at again.
So, distance
What is the total distance travelled by Aman while going from school to garden via home in the following picture?
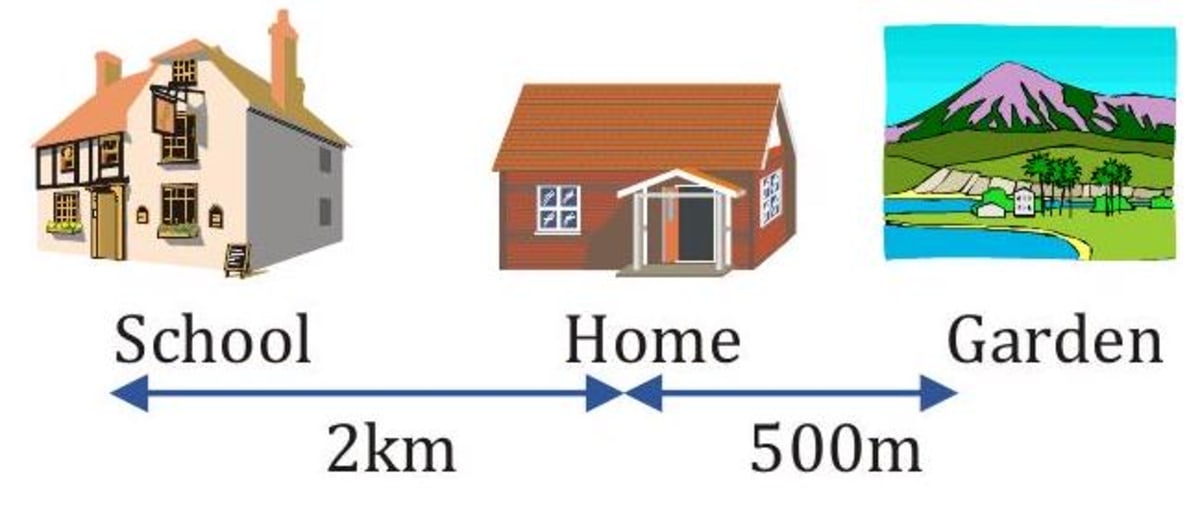
- Solution Distance covered in going from school to home Distance covered in going from home to garden= 500 m Total distance covered
Convert into .
- Solution As Hence,
Convert into Solution As Hence
Manoj covered a distance of 1 km in a running competition, in 50 seconds. Find his running speed.
- Solution Distance covered Time taken seconds Now, Speed
Sumit covers a distance of 2.4 km from his house to reach her college on a scooter. If the Sumit takes 4 min to reach. What is his speed in ?
- Solution Distance covered as . time taken as Hence . Now, Speed Hence speed
A car travels for 10 minutes and 30 seconds. What is this time in seconds?
- Solution Time minutes +30 seconds As 1 minute seconds 10 minutes seconds Total time seconds +30 seconds
A pendulum oscillates 70 times in 35 s . What is the time period of it?
- Solution No. of oscillation Time taken . As, Time period Hence, .
12.0Some Basic Terms
- Suspended : Hanging.
- Orientation : Something related to specified position.
- Stationary : Not moving.
- Equidistant : At equal distance.
- Traversed : Move back and forth and sideways.
- Gravity : A force exerted by the centre of earth.
- Stonehenge : Prehistoric monument having large stone rocks.
- Bob : A simple pendulum consists of a small metal ball called bob suspended by a long thread from a rigid support, such that the bob is free to swing back and forth.
- Timekeeper : an instrument that records or checks the time.
- Bend : A bend is a change in direction.
- Reference point : A reference point is a place or object used for comparison to determine if something is in motion.
- Origin : A point from which a body or an object starts moving.
- Equidistant : Equidistant means being the same or equal distance.
- Odometer: An odometer is an instrument that indicates the distance travelled by a vehicle.
- Ancestors : A person who was in someone's family in past times.