Home
Class 12
PHYSICS
The variation of electric potential for ...

The variation of electric potential for an electric field directed parallel to the x - axis is shown in (Fig. 3.110). Draw the variation of electric field strength with the x- axis.
.

Text Solution

Verified by Experts

The correct Answer is:
.
Promotional Banner

Topper's Solved these Questions

  • ELECTRIC POTENTIAL

    CENGAGE PHYSICS|Exercise Single Correct|56 Videos

  • ELECTRIC POTENTIAL

    CENGAGE PHYSICS|Exercise Multiple Correct|10 Videos

  • ELECTRIC POTENTIAL

    CENGAGE PHYSICS|Exercise Exercise 3.3|9 Videos

  • ELECTRIC FLUX AND GAUSS LAW

    CENGAGE PHYSICS|Exercise MCQ s|38 Videos

  • ELECTRICAL MEASURING INSTRUMENTS

    CENGAGE PHYSICS|Exercise M.C.Q|2 Videos

Similar Questions

Explore conceptually related problems

The electrical potential function for an electrical field directed parallel to the x-axis is shown in the given graph. Draw the graph of electric field strength.

The electrical potential function for an electrical field directed parallel to the x - axis is shown in (Fig. 3.152). . The magnitude of the electric field in the x - direction in the interval 4 le x le 8 is

Due to an electric dipole shown in fig., the electric field intensity is parallel to dipole axis :

Variation of electrostatic potential along the x - direction is shown in (Fig. 3.142). The correct statement about electric field is .

We know that electric field (E ) at any point in space can be calculated using the relation vecE = - (deltaV)/(deltax)hati - (deltaV)/(deltay)hatj - (deltaV)/(deltaz)hatk if we know the variation of potential (V) at that point. Now let the electric potential in volt along the x-axis vary as V = 2x^2 , where x is in meter. Its variation is as shown in figure Draw the variation of electric field (E ) along the x-axis.

The ratio of electric fields on the axis and at equator of an electric dipole will be

The electric field due to a dipole at a distance on its axis is

The law which states that the variations of electric field causes magnetic field is

CENGAGE PHYSICS-ELECTRIC POTENTIAL-Subjective
  1. The variation of electric potential for an electric field directed par...

    Text Solution

    |

  2. If identical charges (-q) are placed at each corner of a cube of side ...

    Text Solution

    |

  3. At s point due to a point charge, the values of electric field intensi...

    Text Solution

    |

  4. Four charges +q, -1, +q and -q are placed in order on the four consecu...

    Text Solution

    |

  5. Water from a tap, maintained at a costant potential V, is allolwed to ...

    Text Solution

    |

  6. Three charges 0.1 coulomb each are placed on the corners of an equila...

    Text Solution

    |

  7. (Figure 3.111). Shows a large conducting ceiling having uniform charge...

    Text Solution

    |

  8. A nonconducting sphere of radius R = 5 cm has its center at the origin...

    Text Solution

    |

  9. Two identical thin ring, each of radius R meters, are coaxially placed...

    Text Solution

    |

  10. Three conducting spherical shells have radii (a, b, and c) such that a...

    Text Solution

    |

  11. (Figure 3.114) shows three concentric spherical conductors A, B, and C...

    Text Solution

    |

  12. Two concentric shells of radii R and 2 R are shown in (Fig. 3.115). In...

    Text Solution

    |

  13. Three charges each of value q are placed at the corners of an equilate...

    Text Solution

    |

  14. A small ball of mass 2 xx 10^-3 kg, having a charge 1 mu C, is suspend...

    Text Solution

    |

  15. Two charges -2Q abd Q are located at the points with coordinates (-3a,...

    Text Solution

    |

  16. A point charge q is located at the centre O of a spherical uncharged c...

    Text Solution

    |

  17. Four point + 8 mu C, -1 mu C, -1 mu C, and + 8 mu C are fixed at the p...

    Text Solution

    |

  18. Charges +q and -q are located at the corners of a cube of side as show...

    Text Solution

    |

  19. Two uniformly charged large plane sheets S1 and S2 having charge densi...

    Text Solution

    |

  20. (Figure 3.118) shows two dipole moments parallel to each other and pla...

    Text Solution

    |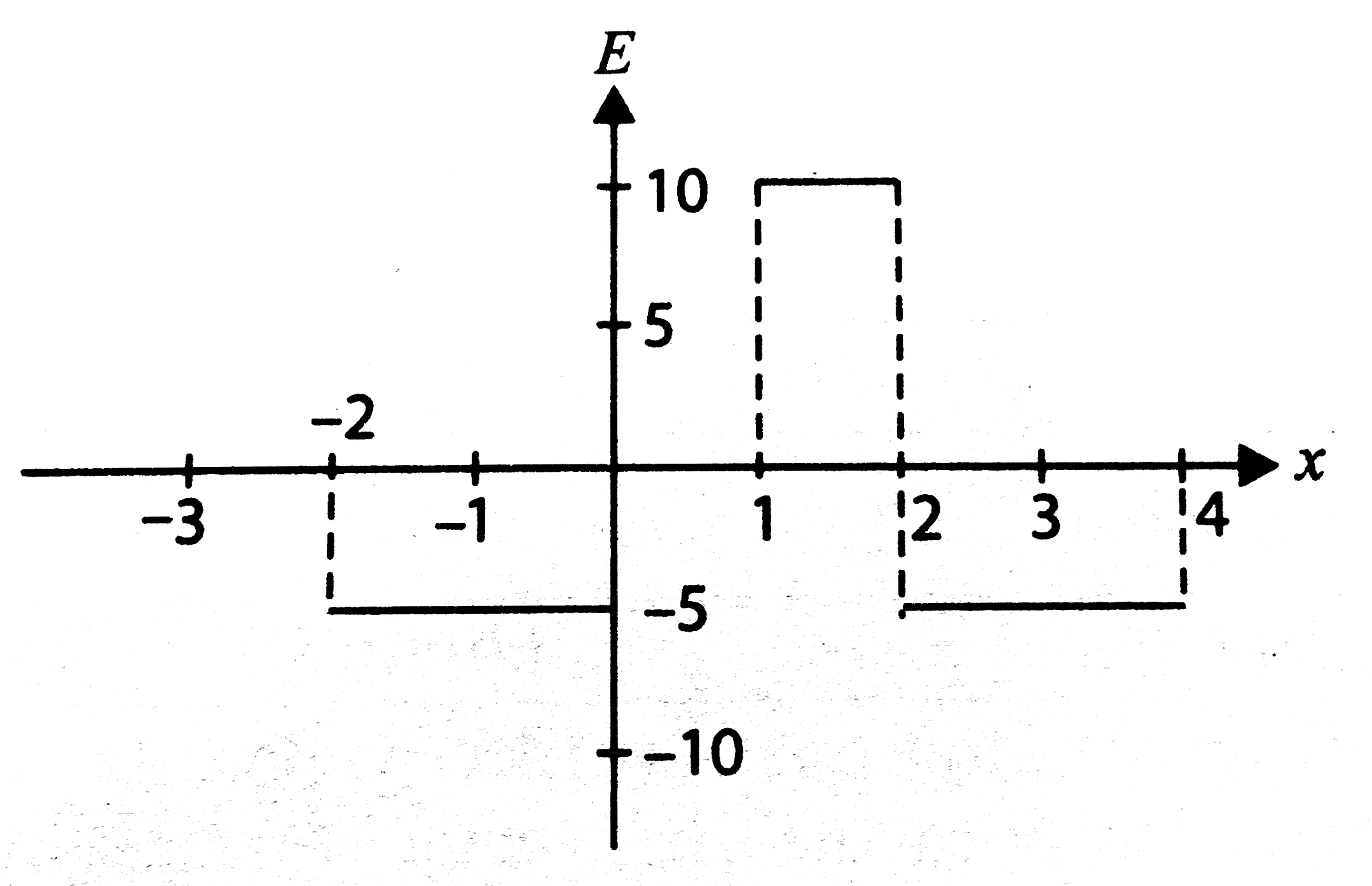