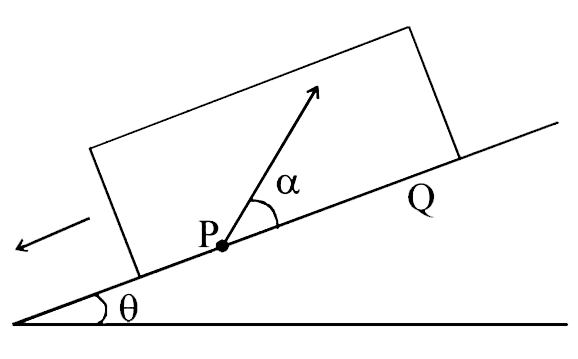
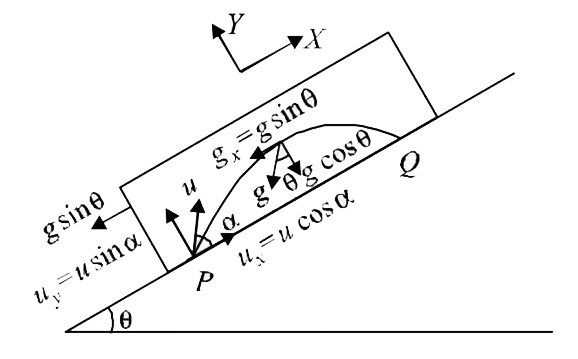
Text Solution
Verified by Experts
The correct Answer is:
Topper's Solved these Questions
Similar Questions
Explore conceptually related problems
SUNIL BATRA (41 YEARS IITJEE PHYSICS)-MOTION-JEE Main And Advanced
- Two towers AB and CD are situated at a distance d apart, as shown in ...
Text Solution
|
- Two guns situated at the top of a hill of height 10 m fire one shot ea...
Text Solution
|
- A large , heavy box is sliding without friction down a smooth plane o...
Text Solution
|
- An object A is kept fixed at the point x= 3 m and y = 1.25 m on a pl...
Text Solution
|
- On a frictionless horizontal surface , assumed to be the x-y plane ,...
Text Solution
|
- STATEMENT -1 : For an observer looking out through the window of a fa...
Text Solution
|
- A train is moving along a straight line with a constant acceleration a...
Text Solution
|
- A ball whose kinetic energy is E , is projected at an angle of 45^@ to...
Text Solution
|
- From a building two balls A and B are thrown such that A is thrown up...
Text Solution
|
- A car , moving with a speed of 50 km//hr , can be stopped by brakes af...
Text Solution
|
- A boy playing on the roof of a 10 m high building throws a ball with a...
Text Solution
|
- The co-ordinates of a moving particle at anytime 't' are given by x =...
Text Solution
|
- A ball is released from the top of a tower of height h metre. It takes...
Text Solution
|
- If vec(A) xx vec(B) = vec(B) xx vec(A), then the angle between A to B ...
Text Solution
|
- A projectile can have the same range 'R' for two angles of projection ...
Text Solution
|
- Which of the following statements is FALSE for a paricle moving in a...
Text Solution
|
- An automobile travelling with a speed 60 km//h , can brake to stop wi...
Text Solution
|
- A ball is thrown from a point with a speed 'v^(0)' at an elevation ang...
Text Solution
|
- A car, starting from rest, accelerates at the rate (f) through a dista...
Text Solution
|
- A particle is moving eastwards with a velocity of 5 ms(-1). In 10 sec...
Text Solution
|