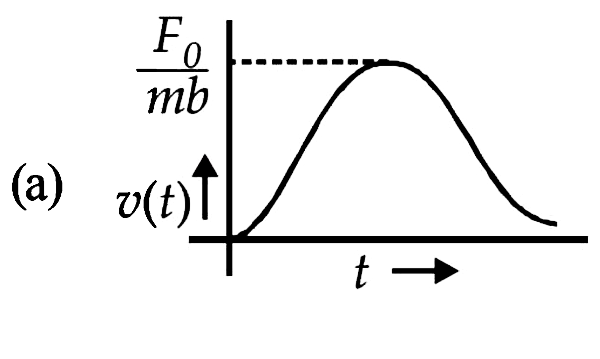
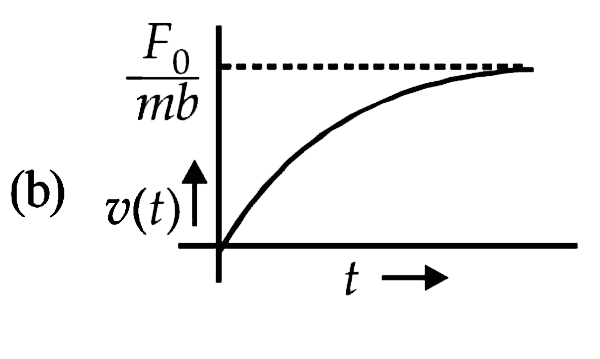
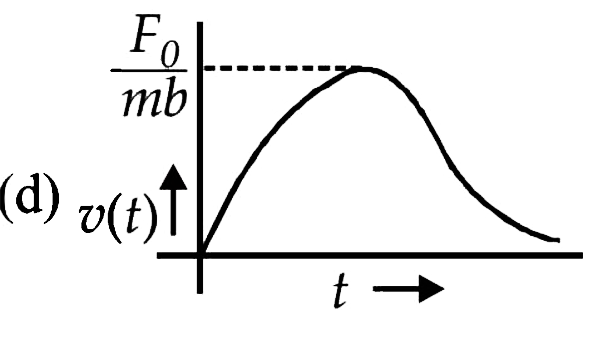
A
B
C
D
Text Solution
AI Generated Solution
The correct Answer is:
Topper's Solved these Questions
Similar Questions
Explore conceptually related problems
SUNIL BATRA (41 YEARS IITJEE PHYSICS)-MOTION-JEE Main And Advanced
- A particle located at x = 0 at time t = 0, starts moving along with t...
Text Solution
|
- A particle is projected at 60(@) to the horizontal with a kinetic ene...
Text Solution
|
- The velocity of a particle is v = v(0) + gt + ft^(2). If its position ...
Text Solution
|
- A body is at rest at x =0 . At t = 0, it starts moving in the posi...
Text Solution
|
- Consider a rubber ball freely falling from a height h = 4.9 m on a hor...
Text Solution
|
- A particle has an initial velocity of 3hat(i) + 4 hat(j) and an accele...
Text Solution
|
- A particle is moving with velocity vecv = k( y hat^(i) + x hat(j)) , ...
Text Solution
|
- A point p moves in counter - clockwise direction on a circular path a...
Text Solution
|
- For a particle in uniform circular motion , the acceleration vec(a) a...
Text Solution
|
- A small particle of mass m is projected at an angle theta with the x...
Text Solution
|
- An object , moving with a speed of 6.25 m//s , is decelerated at a ra...
Text Solution
|
- A water fountain on the ground sprinkles water all around it. If the s...
Text Solution
|
- A boy can throw a stone up to a maximum height of 10 m. The maximum ho...
Text Solution
|
- Two cars of mass m(1) and m(2) are moving in circle of radii r(1) an...
Text Solution
|
- A particle of mass m is at rest the origin at time t= 0 . It is subj...
Text Solution
|
- A projectile is given an initial velocity of ( hat(i) + 2 hat (j) ) m...
Text Solution
|
- From a tower of height H, a particle is thrown vertically upwards wit...
Text Solution
|
- Two stones are thrown up simultaneously from the edge of a cliff 240...
Text Solution
|
- Airplanes A and B are flying with constant velocity in the same vertic...
Text Solution
|
- A rocket is moving in a gravity free space with a constnat acceleratio...
Text Solution
|