A
B
C
D
Text Solution
Verified by Experts
The correct Answer is:
Topper's Solved these Questions
Similar Questions
Explore conceptually related problems
SUNIL BATRA (41 YEARS IITJEE PHYSICS)-SIMPLE HARMONIC MOTION-JEE Main And Advanced
- The period of oscillation of a simple pendulum of length (L) suspended...
Text Solution
|
- A particle executes simple harmonic motion between x = -A and x = + A....
Text Solution
|
- For a particle executing (SHM) the displacement (x) is given by (x = A...
Text Solution
|
- A simple pendulum has time period T1. The point of suspension is now m...
Text Solution
|
- The (x - t) graph of a particle undergoing simple harmonic motion is s...
Text Solution
|
- A uniform rod of length L and mass M is pivoted at the centre. Its two...
Text Solution
|
- The mass M shown in the figure oscillates in simple harmonic motion wi...
Text Solution
|
- A point mass is subjected to two simultaneous sinusoidal displacements...
Text Solution
|
- A small block is connected to one end of a massless spring of un - str...
Text Solution
|
- A particle executes simple harmonic motion with a frequency f. The fre...
Text Solution
|
- A linear harmonic oscillator of force constant 2 xx 10^6 N//m and ampl...
Text Solution
|
- A uniform cylinder of length (L) and mass (M) having cross sectional a...
Text Solution
|
- A highly rigid cubical block A of small mass M and slide L is fixed ri...
Text Solution
|
- One end of a long metallic wire of length (L) is tied to the ceiling. ...
Text Solution
|
- A particle of mass (m) is executing oscillations about the origin on t...
Text Solution
|
- Three simle harmionic motions in the same direction having the same am...
Text Solution
|
- The function x = A sin^2 (omega)t + B cos^2 (omega)t + Csin (omega)t c...
Text Solution
|
- A metal rod of length 'L' and mass 'm' is pivoted at one end. A thin d...
Text Solution
|
- Two independent harmonic oscillators of equal mass are oscillating abo...
Text Solution
|
- A block with mass (M) is connected by a massless spring with stiffness...
Text Solution
|
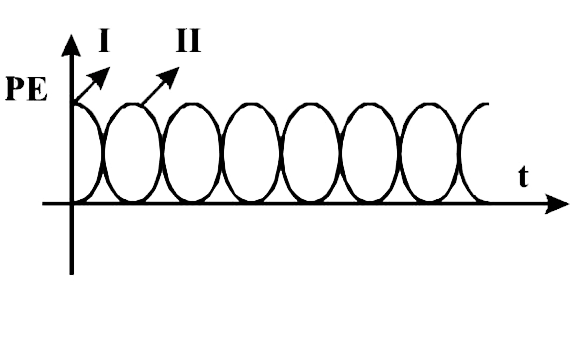 ,
, 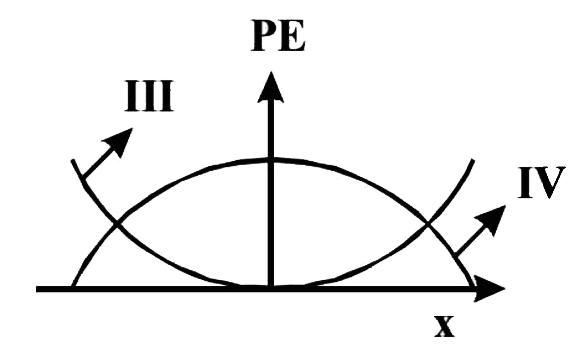 .
.