Home
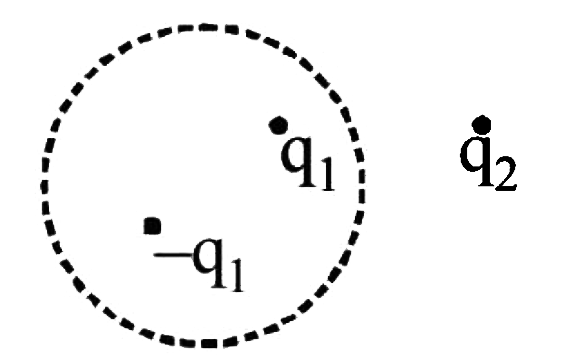
Class 12
PHYSICS
A Gausisan surface in the figure is show...

A Gausisan surface in the figure is shown by dotted line.
The electric field on the surface will be

A

(a) due to `q_1` and `q_2` only

B

(b) due to `q_2` only

C

(c) `zero`

D

(d) due to all

Text Solution

Verified by Experts

The correct Answer is:
D
The flux through the Gausisan surface is due to the charges inisde the Gausisan surface. But the electric field on the Gausisan surface will be due to the charges present in the isde the Gausisan surface and outisde it. It will be due to all the charges.
Promotional Banner

Topper's Solved these Questions

  • ELECTROSTATICS

    SUNIL BATRA (41 YEARS IITJEE PHYSICS)|Exercise Subjective Problems|2 Videos

  • ELECTROSTATICS

    SUNIL BATRA (41 YEARS IITJEE PHYSICS)|Exercise Comprehension Based Questions|2 Videos

  • ELECTROMAGNETIC INDUCTION AND ALTERNATING CURRENT

    SUNIL BATRA (41 YEARS IITJEE PHYSICS)|Exercise JEE Main And Advanced|107 Videos

  • MODERN PHYSICS

    SUNIL BATRA (41 YEARS IITJEE PHYSICS)|Exercise MCQ (One Correct Answer|1 Videos

Similar Questions

Explore conceptually related problems

A Gaussian surface in the fig. is shown by dotted line. The electric field on the surface will be :-

A Gaussian surface encloses a proton p. The electric field at any point on the surface is vec€ . The flux linked with the Gaussian surface is phi . STATEMENT-1 : When an electron is kept close to this system outside the Gaussian surface, the flux linked with the surface would change. and STATEMENT-2 : The presence of electron will alterthe electric field on the gaussian surface.

Consider the charge configuration and a spherical Gaussian surface as shown in the figure. When calculating the flux of the electric field over the spherical surface, the electric field will be due to.

If the flux of the electric field through a closed surface is zero,

If the net electric field flux passing through a closed surface is zero, then the electric field at the surface will be

The black shapes in the figure below are closed surfaces. The electric field lines are in red. For which case the net flux through the surfaces is non-zero ?

A spherical charged conductor has sigma as the surface density of charge. The electric field on its surface is E. If the radius of the sphere is doubled keeping the surface density of charge unchanged, what will be the electric field on the surface of the new sphere -

If the total charge enclosed by a surface is zero, does it imply that the electric field everywhere on the surface is zero ? Conversely, if the electric field everywhere on a surface is zero, does it imply that net charge inside is zero.

Some equipotential surface are shown in the figure. Find the value of electric field :-