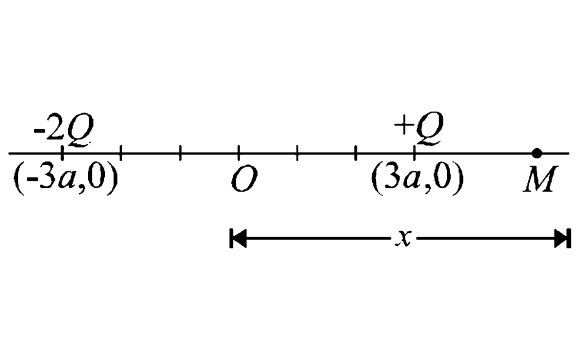Two charges `-2Q` abd `Q` are located at the points with coordinates `(-3a, 0)` and `(+3a, 0)` respectively in the x-y plane. (i) Show that all points in the x-y plane where the electric potential due to the charges is zero, on a circle. Find its radius and the location of its centre (ii) Give the expression V(x) at a general point on the x-axis and sketch the function V(x) on the whole x-axis. (iii) If a particle of charge +q starts from rest at the centre of the circle, shown by a short quantitative argument that the particle eventually crosses the circule. Find its speed when it does so.

Answer

A, B, C, D

Explanation

Let P be a point in the X-Y plane with coordinates (x,y) at which the potential due to charges `-2Q` and `+Q` placed at A and B respectively be zero.

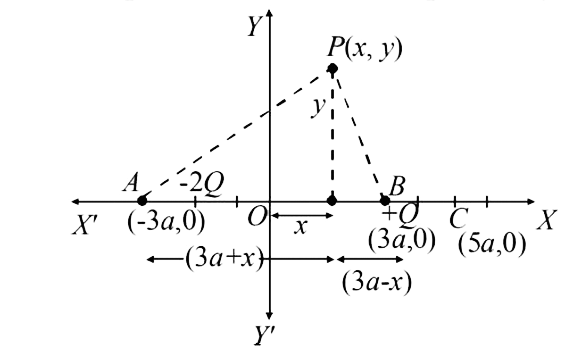
`:.` `(K(2Q))/(sqrt((3a+x)^2+y^2))=(K(+Q))/(sqrt((3a-x)^2+y^2)`
`implies 2sqrt((3a-x)^2+y^2)=sqrt((3a+x)^2+y^2)`
`implies (x-5a)^2+(y-0)^2=(4a)^2`
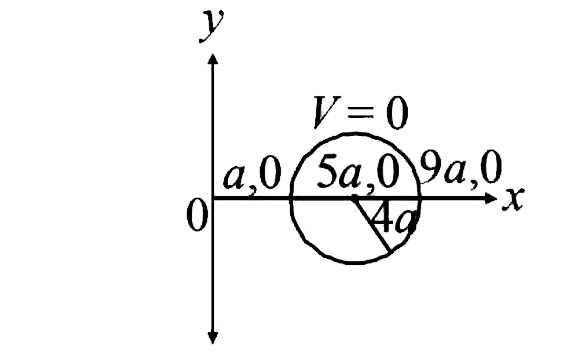
This is the equation of a circle with centre at `(5a, 0)` and radius `4a`. Thus C `(5a, 0)` is the centre of the circle.
(b) For xgt3a
To find V(x) at any point on X-axis, let us consider a point (arbitrary) M at a distance x from the origin.

The potential at M will be
`V(x)=(K(-2Q))/(x+3a)+(K(+Q))/((x-3a))` where `k=(1)/(4piepsilon_0)`
`:.` `V(x)=KQ[(1)/(x-3a)-(2)/(x+3a)]` for `|x|gt3a`
Similarly, for `0lt|x|lt3a`
`V(x)=KQ[(1)/(3a-x)-(2)/(3a+x)]`
Since circle of zero potential cuts the x-axis at (a,0) and (9a,0)
Hence, `V(x)=0` at `x=a`, at `x=9a`
* From the above expressions
`V(x)rarroo` at `xrarr3a` and `V(x)rarr-oo` at `xrarr-3a`
* `V(x)rarr0` as `xrarr+-oo`
* V(x) varies 1/x in general.

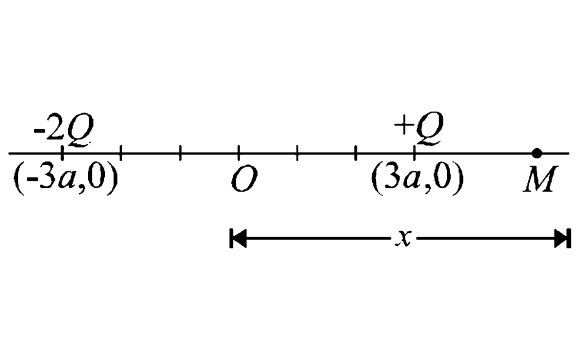
(c) Applying Energy Conservation
`(K.E.+P.E.)_(centre)=(K.E.+P.E.)_(c ircumference)`
`0+K[(Qq)/(2a)-(2Qq)/(8a)]=1/2mv^2+K[(Qq)/(6a)-(2Qq)/(12a)]`
`1/2mv^2=(KQq)/(4a)`, `v=sqrt((KQq)/(2ma))=sqrt((1)/(4piepsilon_0)((Qq)/(2ma)))`
` (##JMA_El_C12_087_S04.png" width="80%">