The capacitance of a parallel plate capacitor with plate area `A` and separation `d` is `C`. The space between the plates in filled with two wedges of dielectric constants `K_(1)` and `K_(2)` respectively. Find the capacitance of resulting capacitor.

Answer

A, B, D

Explanation

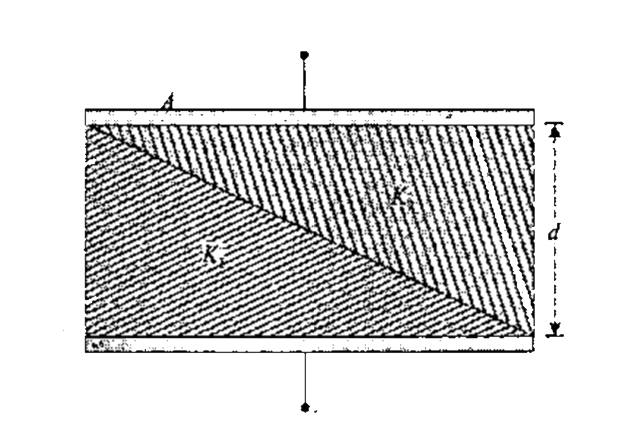
Case (i) When no dielectric:
Given `C=(epsilon_0A)/(d)`
Case (ii) When dielectric is filled: A small dotted element of thickness dx is considered as shown in the figure.

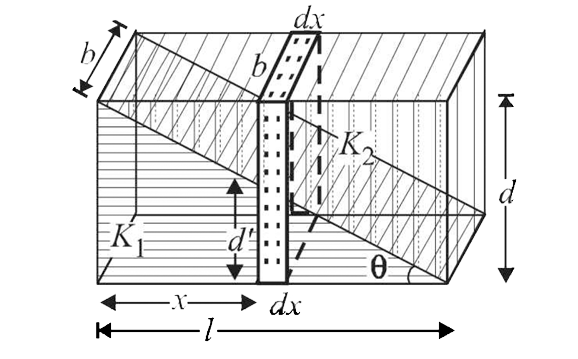
The small capacitance of the dotted portion `(1)/(dC)=(1)/(dC_1)+(1)/(dC_2)` where `dC_1=` capacitance of capacitor with dielectric `K_1`
`dC_2=` capacitance of capacitor with dielectric `K_2`.
Let l,b the length and breath of the capacitor plate.
Therefore `lxxb=A`.
`dC_1=(K_1(bdx)epsilon_0)/(d^')`
`d^'=d-x(d)/(l)=d[1-x/l]`
`:.` `dC_1=(K_1b(dx)epsilon_0)/(d[1-x/l])-(K_1bl(dx)epsilon_0)/(d(l-x))=(K_1Aepsilon_0(dx))/(d(l-x))`
Similarly, `dC_2=(K_2epsilon_0(bdx))/(d-d^')=(K_2epsilon_0bdx)/(d-d+(xd)/(l))`
`(K_2epsilon_0bldx)/(xd)=(K_2epsilon_0Adx)/(xd)`
`:.` `(1)/(dC)=(d(l-x))/(K_1Aepsilon_0(dx))+(xd)/(K_2Aepsilon_0(dx))`
`implies (K_1K_2Aepsilon_0dx)/(K_2ld+d(K_1-K_2)x)=dC`
To find the capacitance of the whole capacitor, we integrate the above equation.
`C=int_0^t(K_1K_2Aepsilon_0dx)/(K_2ld+d(K_1-K_2)x)`
`=K_1K_2Aepsilon_0int_0^l(dx)/(K_2ld+d(K_1-K_2)x)`
`=K_1K_2Aepsilon_0[(log[K_2ld+d(K_1-K_2)x])/(d(K_1-K_2))]_0^l`
`C=(K_1K_2Aepsilon_0)/(d(K_1-K_2))log(K_1/K_2)`