Two capacitors `A` and `B` with capacities `3muF` and `2muF` are charged to a potential difference of `100 V` and `180V`, respectively. The plates of the capacitors are connected as show in figure with one wire of each capacitor free. The upper plate of `A` is positive and that of `B` is negastive. An uncharged `2muF` capcitor `C` with lead wires falls on the free ends to complete the circuit. Calculate
a. the final charge on the three capacitors.
b. the amount of electrostatic energy stored in the system before and after completion of the circuit.

Answer

A, B, C, D

Explanation

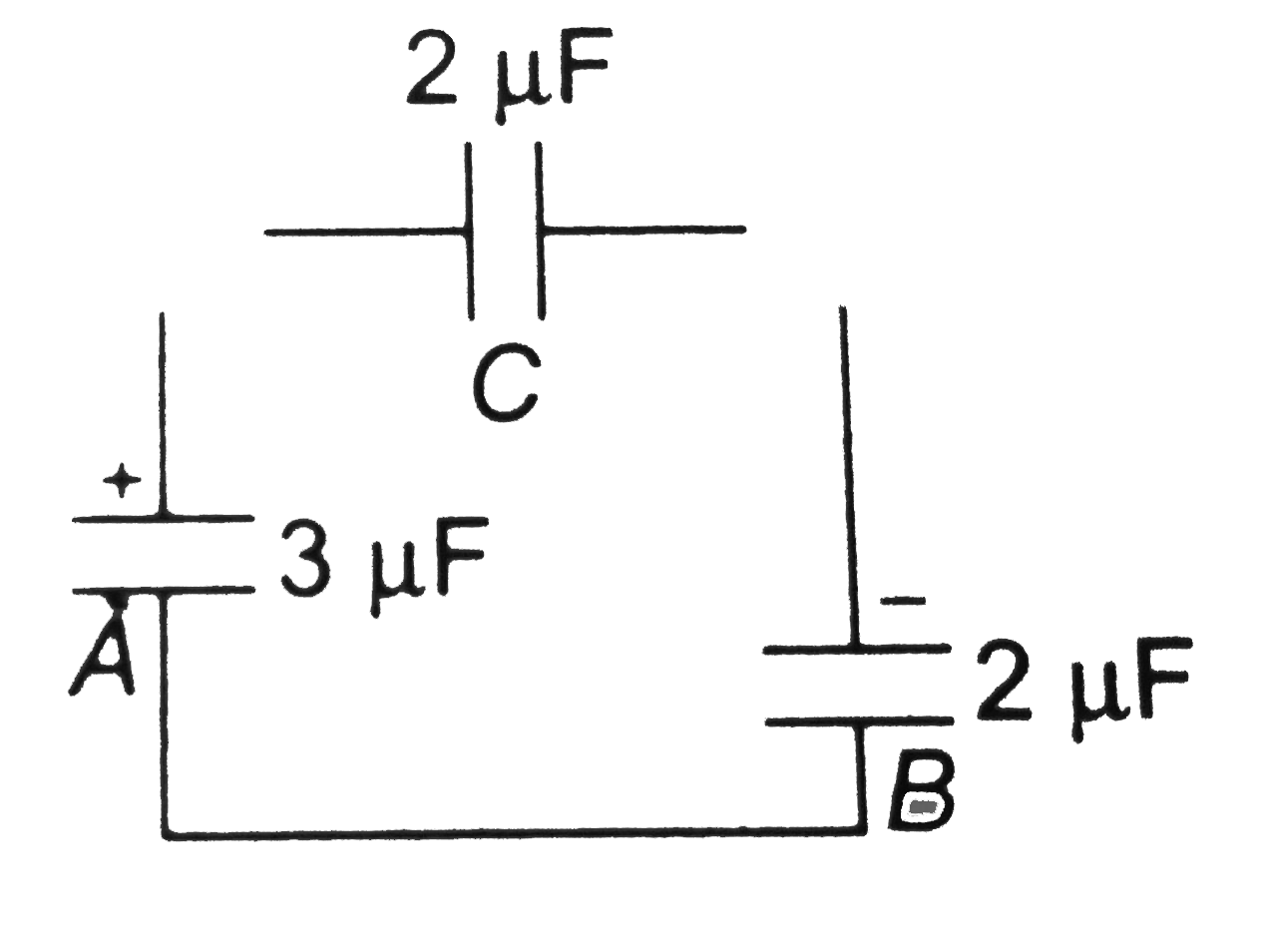
(i) KEY CONCEPT: Use charge conservation to solve this problem.
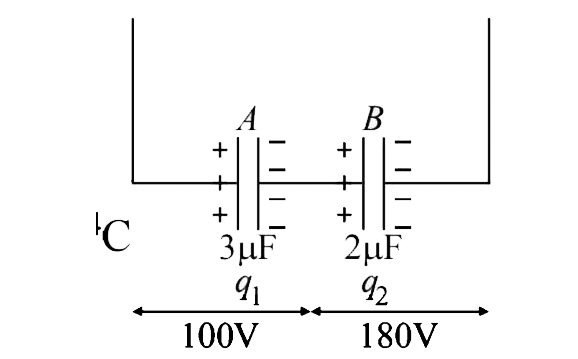
INITIALLY:
Charge on capacitor A
`q_A=3xx10^-6xx100=3xx10^4C`
Charge on capacitor B
`q_B=2xx10^-6xx180=3.6xx10^-4C`

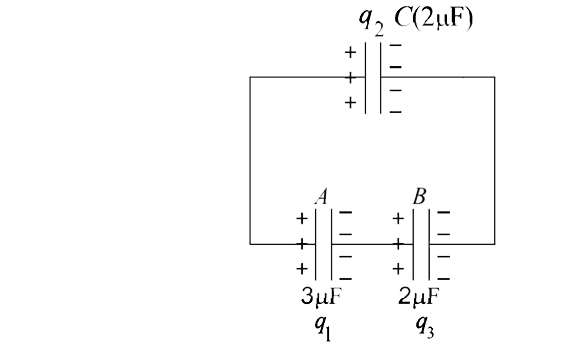
FINALLY:
Let the charge on capacitor A, C and B be `q_1, q_2` and `q_3` respectively.
By charge conservation.
The sum of charge on +ve plate of capacitor A and C should be equal to `q_A`.
`:.` `q_1+q_2=3xx10^-4C` ...(i)
Similarly the sum of charge on -ve plates of capacitor C and B will be equal to `q_B`
`:.` `-q_2-q_3=-3.6xx10^-4C`
`implies q_2+q_3=3.6xx10^-4C` ...(ii)
Applying Kirchoff's law in the closed loop, we get
`(q_1)/(3xx10^-6)-(q_2)/(2xx10^-6)+(q_3)/(2xx10^-6)=0`
`implies 2q_1-3q_2+3q_3=0` ...(iii)
On solving (i), (ii) and (iii), we get
`q_1=90xx10^-6C`, `q_2=210xx10^-6C`, and `q_3=150xx10^-6C`,

(ii) Amount of electrostatic energy in the system initially
`U_i=U_A+U_B=1/2C_A(V_A)^2+1/2C_B(V_B)^2`
`=1/2xx3xx10^-6(100)^2+1/2xx2xx10^-6(180)^2`
`=4.74xx10^-2J`
Amount of electrostatic energy stored finally
`U_f=1/2(q_1^2)/(C_A)+1/2(q_2^2)/(C_B)+1/2(q_3^2)/(C_C)`
`=1/2((90xx10^-6)^2)/(3xx10^-6)+1/2((210xx10^-6)^2)/(2xx10^-6)+1/2((150xx10^-6)^2)/(2xx10^-6)+1/2((150xx10^-6)^2)/(2xx10^-6)=1.8xx10^-2J`