Let the particle at some instant be at a point P distant x from the origin. As shown in the figure, there are two forces of repulsion acting due to two charges of +8 mC. The net force is `2F cos alpha` towards light.
Similarly there are two forces of attraction due to two charges of `-1 mC`. The net force due to these force is `2F cos beta` towards left.
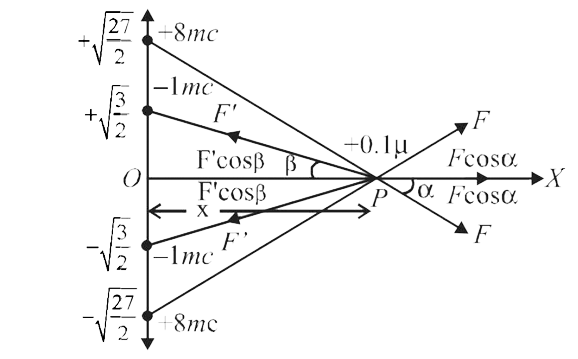
The net force on charge `0.1 muC` is zero when
`2F cos alpha=2F^' cos beta`
`(Kxx8xx10^-6xx0.1xx10^-6)/(sqrt(x^2+27/2))^2xx(x)/(sqrt(x^2+27/2))`
`=(Kxx1xx10^-6xx0.1xx10^-6)/(sqrt(x^2+3/2))^2xx(x)/(sqrt(x^2+3/2))`
`implies x=+-sqrt(5/2)`
This means that we need to move the charge from `-oo` to `sqrt(5/2)` . Thereafter the attractive forces will make the charge move to origin.
The electric potential of the four charges at `x=sqrt(5/2)` is
`V=(2xx9xx10^9xx8xx10^-6)/(sqrt(5/2)+27/2)`-(2xx9xx10^9xx10^-6)/(sqrt(5/2)+3/2)`
`=2xx9xx10^9xx10^-6[8/4-1/2]=2.7xx10^4V`
Kinetic energy is required to overcome the force of repulsion from `prop` to `x=sqrt(5/2)`.
The work done in this process is `W=q(V)`
where V=p.d between `oo` and `x=sqrt(5/2)`.
`:.` `W=0.1xx10^-6xx2.7xx10^4=2.7xx10^-3J`
By energy conservation `1/2mV_0^2=2.7xx10^-3`
`implies 1/2xx6xx10^-4V_0^2=2.7xx10^-3`
`implies V_0=3m//s`
K.E. at the origin
Potential at origin `V_(x=0)=(2xx9xx10^9xx8xx10^-6)/(sqrt(27/2))-(2xx9xx10^9xx10^-6)/(sqrt(3/2))`
`=2.4xx10^4`
Again by energy conservation
`K.E. =q[V_(x=(sqrt5)/(2))-V_(x=0)]`
`:.` K.E. =0.1xx10^-6[2.7xx10^4-2.4xx10^4]`
`=0.1xx10^-6xx0.3xx10^4`
`=3xx10^-4J`
