Home
Class 12
MATHS
If A (bara) and B (barb) are any two p...

If ` A (bara) and B (barb) ` are any two points in the space
and ` R(barr)` be a point on the line segment AB
dividing it internally in the ratio m : n , then prove that :
`barr = (mbarb + nbara)/(m + n)`

Text Solution

Verified by Experts

As R is point on line segment AB (A - R - B ) and
` (AR)/(RB) = (m)/(n)`

` therefore m (RB) = n (AR) and bar(AR) and bar(AB) ` are in same direction .
` therefore m ((bar(RB)) = n (bar(AR))`
` rArr m (bar(OB) - bar(OR)) = n (bar(OR) - bar(OA)) `
` rArr m (barb - barr) = n (barr - bara)`
`rArr mbarb- mbarr = nbarr - nbara `
`rArr mbarb+ nbara = mbarr + n^(2)`
` rArr barr = (mbarb + nbara)/(m + n)` Hence Proved
Promotional Banner

Topper's Solved these Questions

  • MARCH 2019

    GURUKUL PUBLICATION - MAHARASHTRA PREVIOUS YEAR PAPERS|Exercise SECTION-D|13 Videos

  • MARCH 2019

    GURUKUL PUBLICATION - MAHARASHTRA PREVIOUS YEAR PAPERS|Exercise SECTION-B|10 Videos

  • MARCH 2018

    GURUKUL PUBLICATION - MAHARASHTRA PREVIOUS YEAR PAPERS|Exercise SECTION - II|20 Videos

  • OCTOBER 2014

    GURUKUL PUBLICATION - MAHARASHTRA PREVIOUS YEAR PAPERS|Exercise SECTION - II|19 Videos

Similar Questions

Explore conceptually related problems

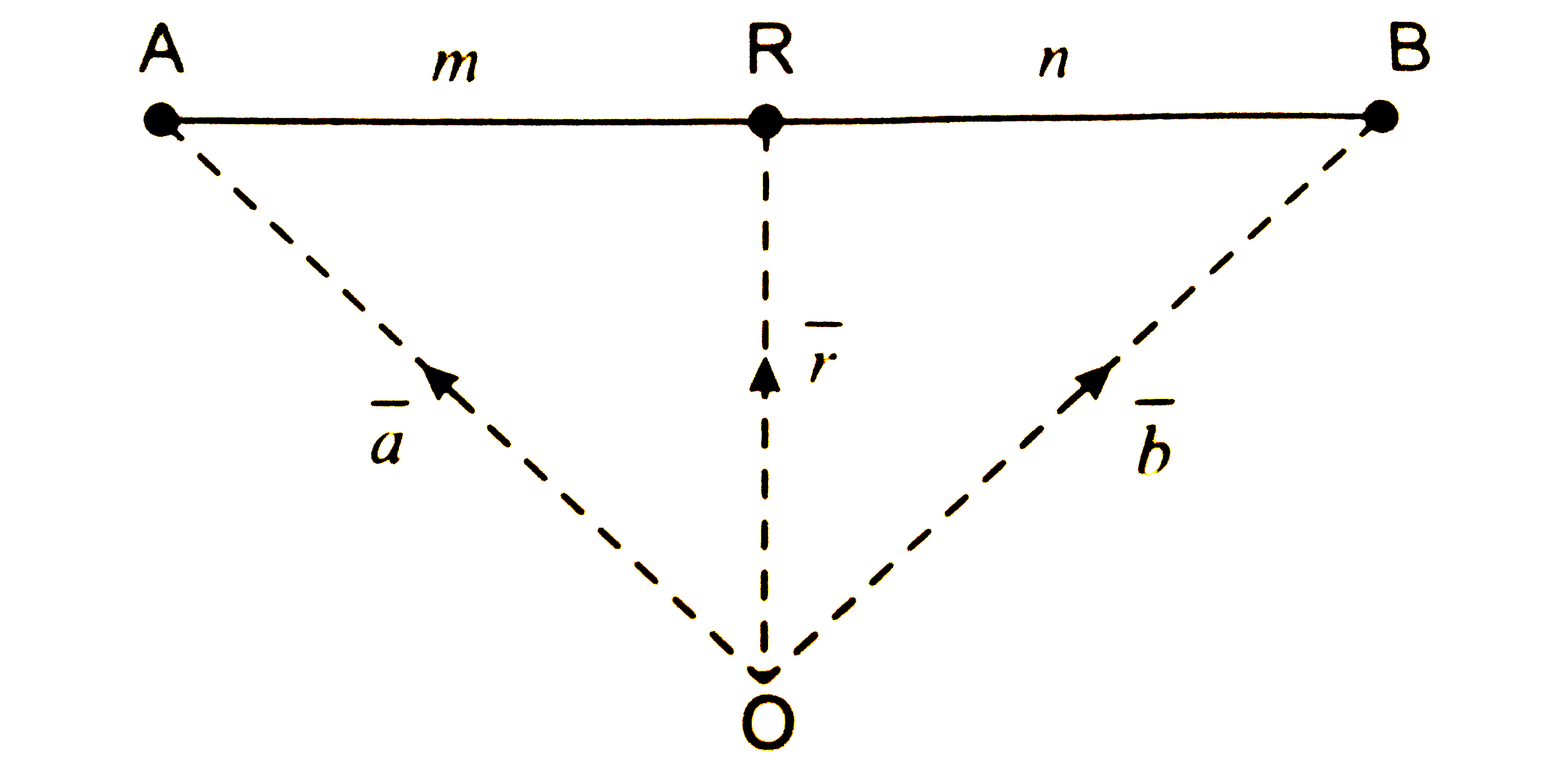
Let A(bara) and B(barb) be any two points in the space and R(barr) be a point on the line segment AB dividing it internally in the ration m : n the prove that barr = (mbarb+ nbara)/(m+n) . Hence find the position vector of R which divides the line segment joining the point A(1,-2,1) and B(1,4,-2) internally in the ratio 2: 1 .

If point C ( barc) divides the segment joining the point A (bara) and B (barb) internally in the ratio m : n, then prove that barc = (mbarb + nbara)/(m+n).

If A(3,1,-2) and B(1,-3,-1) be two points find the coordinates coordinates of the point which divides the line segment AB. Internally in the ratio 1:3

If the point barP (barp) =bara+ 2barb and the point A(bara) divides seg PQ internally in the ratio 2: 3, then : Q(barq) =

The position vectors of the point which divides internally in the ratio 2:3 the join of the points 2bara-3barb and 3bara-2barb , is

Write the coordinates of the point dividing line segment toining points (2,3) and (3,4) internally in the ratio 1:5 .

Find the coordinates of the point which divides the line segment joining (-1,3) and (4,-7) internally in the ratio 3:4 .

A line segment AB is divided at point P such that PB : AB = 3:7, then the ratio of AP : PB = ________.

Write the coordinates ot the point dividing line segment joining the points (1, 5) and (-5,1) internally in the ratio 1: 4.