Similar Questions
Explore conceptually related problems
Recommended Questions
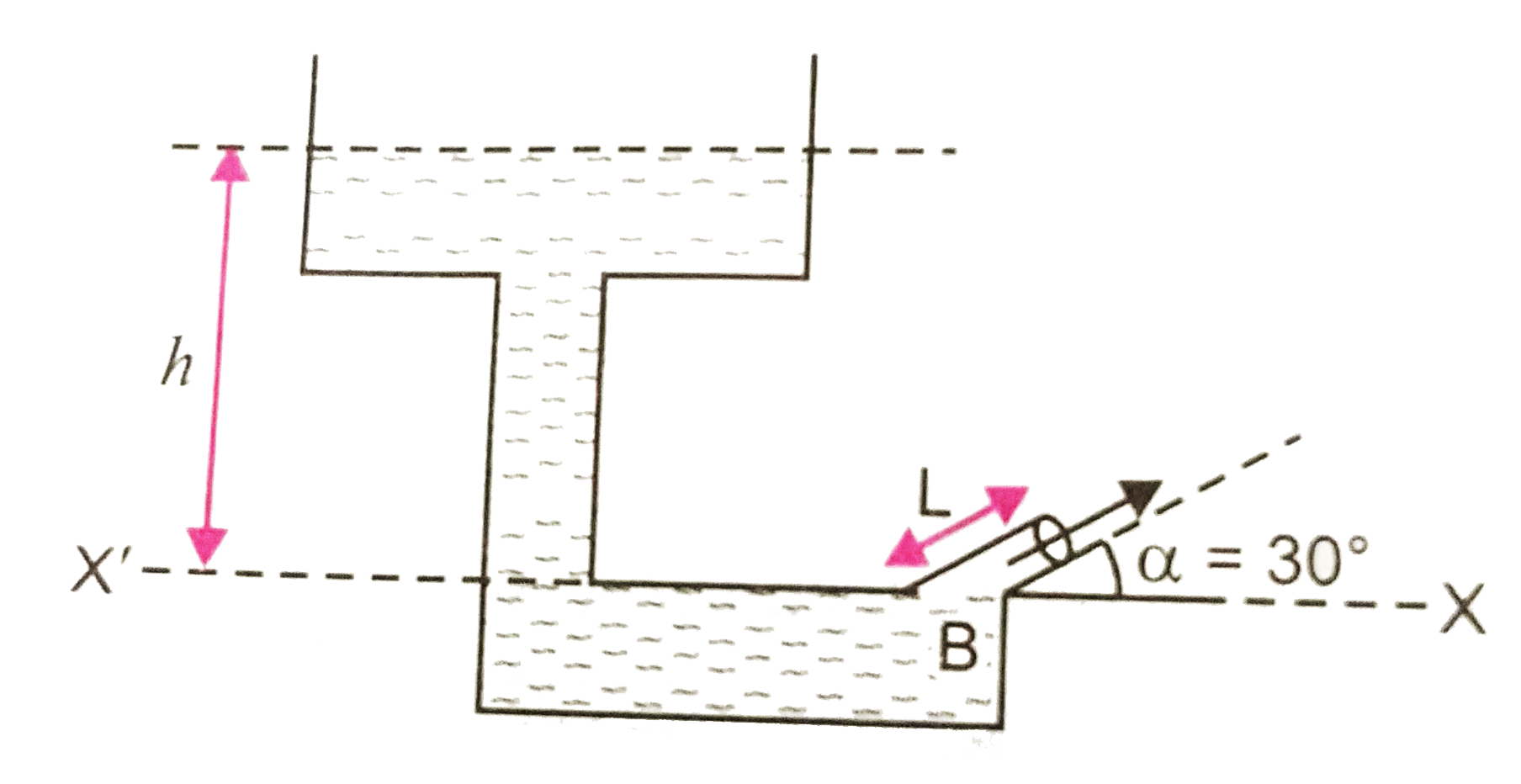
- Determine the hight above the dashed line XX' attained by the water st...
Text Solution
|
- A metallic sphere of radius 1.0 xx 10^(-3) m and density 1.0 xx 10^(4)...
Text Solution
|
- Determine the hight above the dashed line XX' attained by the water st...
Text Solution
|
- There is a small hole of diameter 0.1 mm at the bottom of a large cont...
Text Solution
|
- धारा की चाल 5 कि. मी./घंटा है। एक मोटरबोट धारा के प्रतिकूल 10 कि. मी. ...
Text Solution
|
- शांत जल में एक व्यक्ति 3 कि. मी./घंटे की चाल से तैर सकता है। यदि धारा ...
Text Solution
|
- The pressure at a point in water is 10 N//m^(2). The depth below this ...
Text Solution
|
- Find the slope of the lines passing through the given points L(-2, -...
Text Solution
|
- To construct a line parallel to a given line and passing through a giv...
Text Solution
|