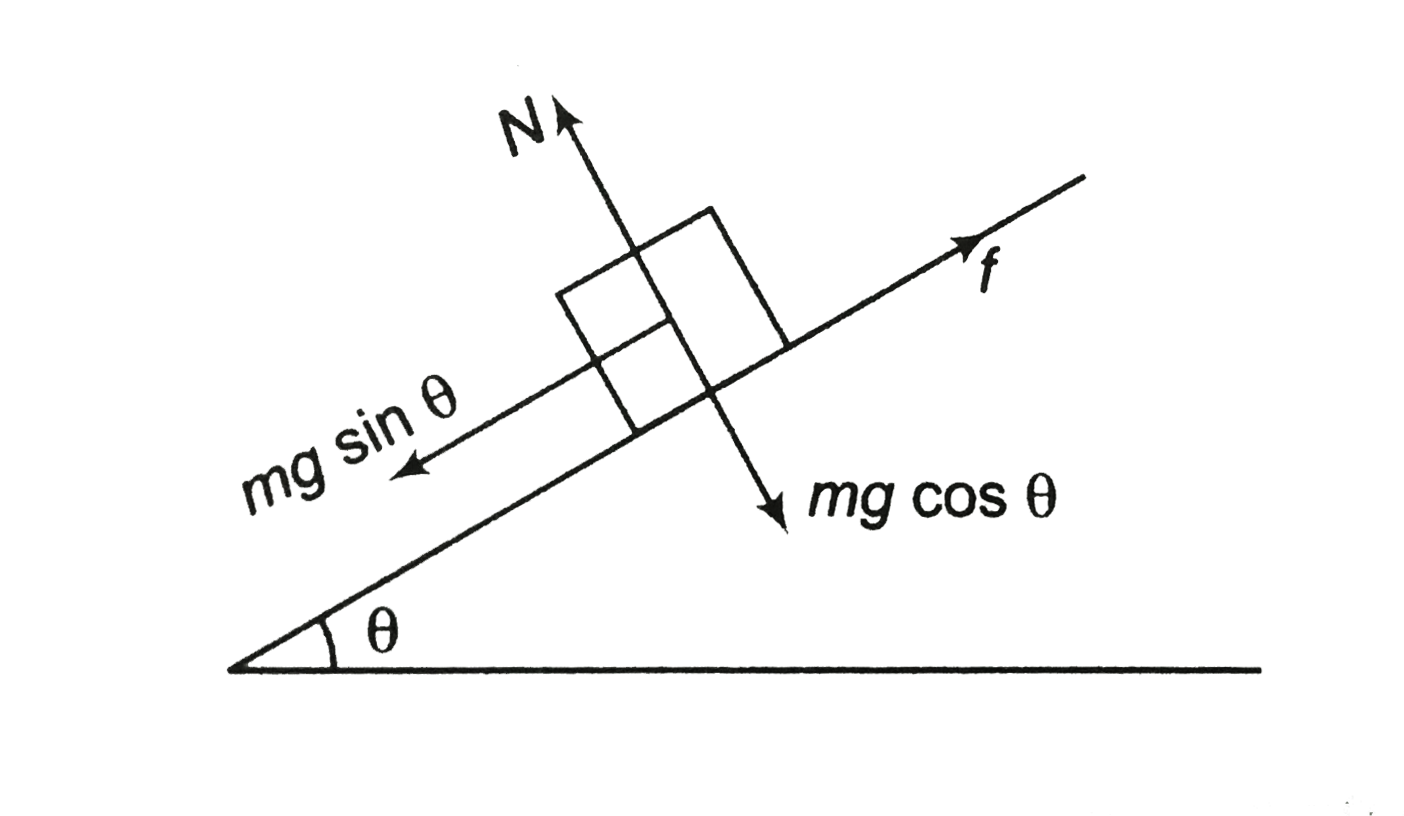
Text Solution
Verified by Experts
Similar Questions
Explore conceptually related problems
Recommended Questions
- A partical of mass 1kg rests on rought contact with a plane inclined a...
Text Solution
|
- A partical of mass 1kg rests on rought contact with a plane inclined a...
Text Solution
|
- A partical of mass 1kg and carrying 0.01C is at rest on an inclined pl...
Text Solution
|
- A body takes just twice the time as long to slide down a plane incline...
Text Solution
|
- A block of mass m rests on a rough inclined plane. The coefficient of ...
Text Solution
|
- The two blocks A and B of equal mass are initially in contact when rel...
Text Solution
|
- An inclined plane is inclined at an angle theta with the horizontal. A...
Text Solution
|
- A mass placed on an inclined plane is just in equilibrium. If mu is th...
Text Solution
|
- A body of mass 10kg is on a rough inclined plane having an inclination...
Text Solution
|