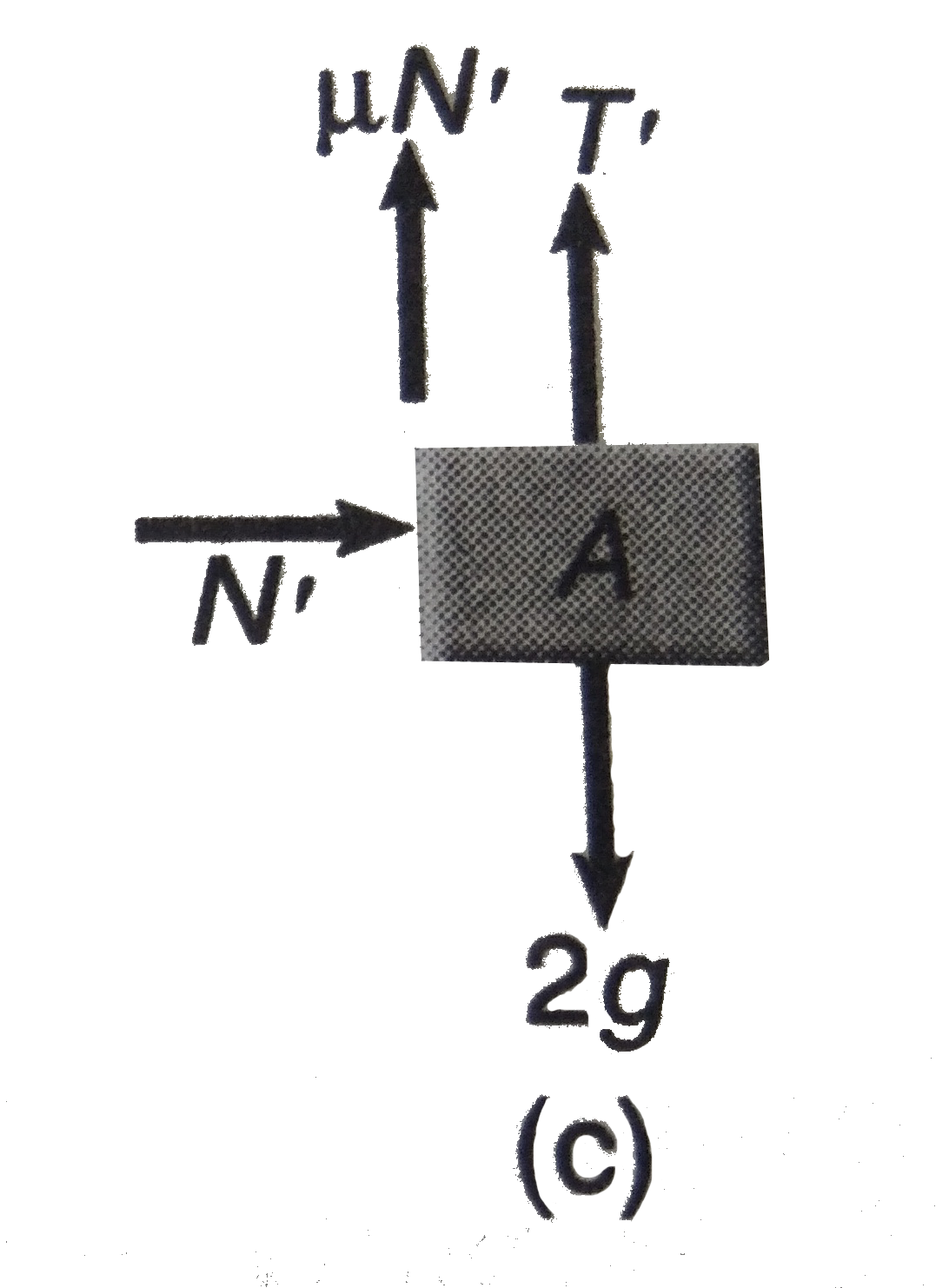
Text Solution
Verified by Experts
The correct Answer is:
Topper's Solved these Questions
WORK, ENERGY & POWER
DC PANDEY|Exercise Exercise 9.1|10 VideosWORK, ENERGY & POWER
DC PANDEY|Exercise Exercise 9.2|9 VideosWORK, ENERGY & POWER
DC PANDEY|Exercise TYPE2|1 VideosWAVE MOTION
DC PANDEY|Exercise Integer Type Question|11 VideosWORK, ENERGY AND POWER
DC PANDEY|Exercise MEDICAL ENTRACES GALLERY|33 Videos
Similar Questions
Explore conceptually related problems
DC PANDEY-WORK, ENERGY & POWER-Miscellaneous Example
- A small mass m starts from rest and slides down the smooth spherical s...
Text Solution
|
- A smooth track in the form of a quarter-circle of radius 6 m lies in t...
Text Solution
|
- A single conservative force F(x) acts on a on a (1.0kg ) particle that...
Text Solution
|
- A small disc A slides down with initial velocity equal to zero from th...
Text Solution
|
- A small disc of mass m slides down a smooth hill of height h without i...
Text Solution
|
- Two blocksA andB are connected to each other by a string and a spring ...
Text Solution
|
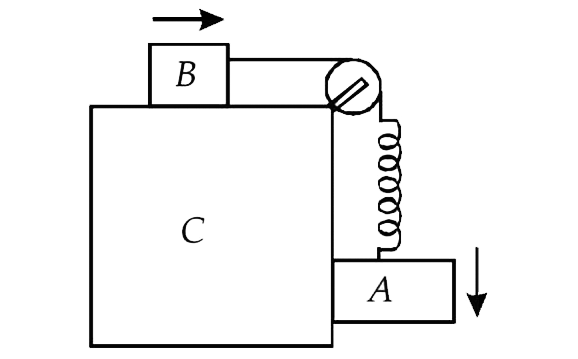
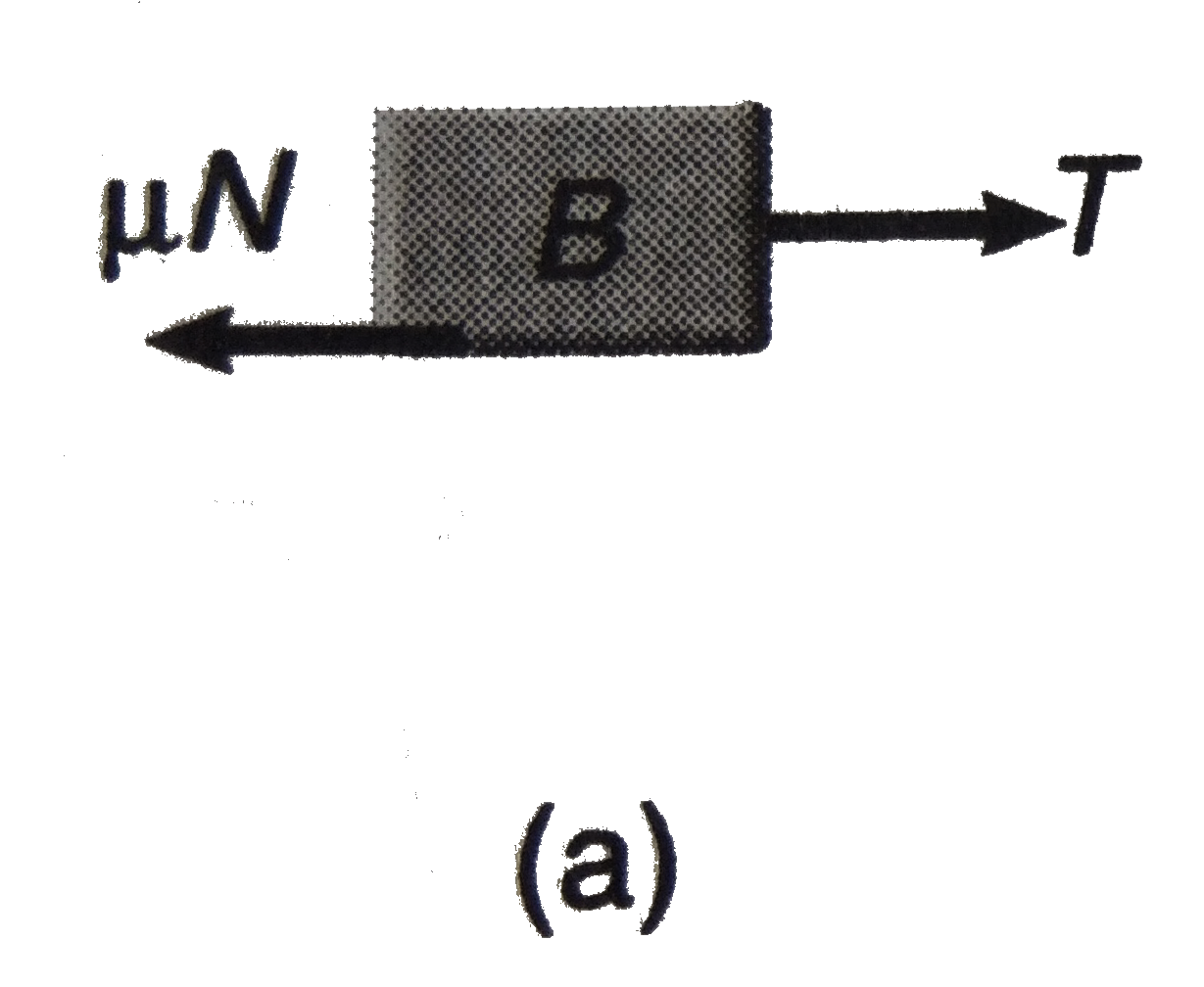 .
.