Text Solution
Verified by Experts
The correct Answer is:
Similar Questions
Explore conceptually related problems
Recommended Questions
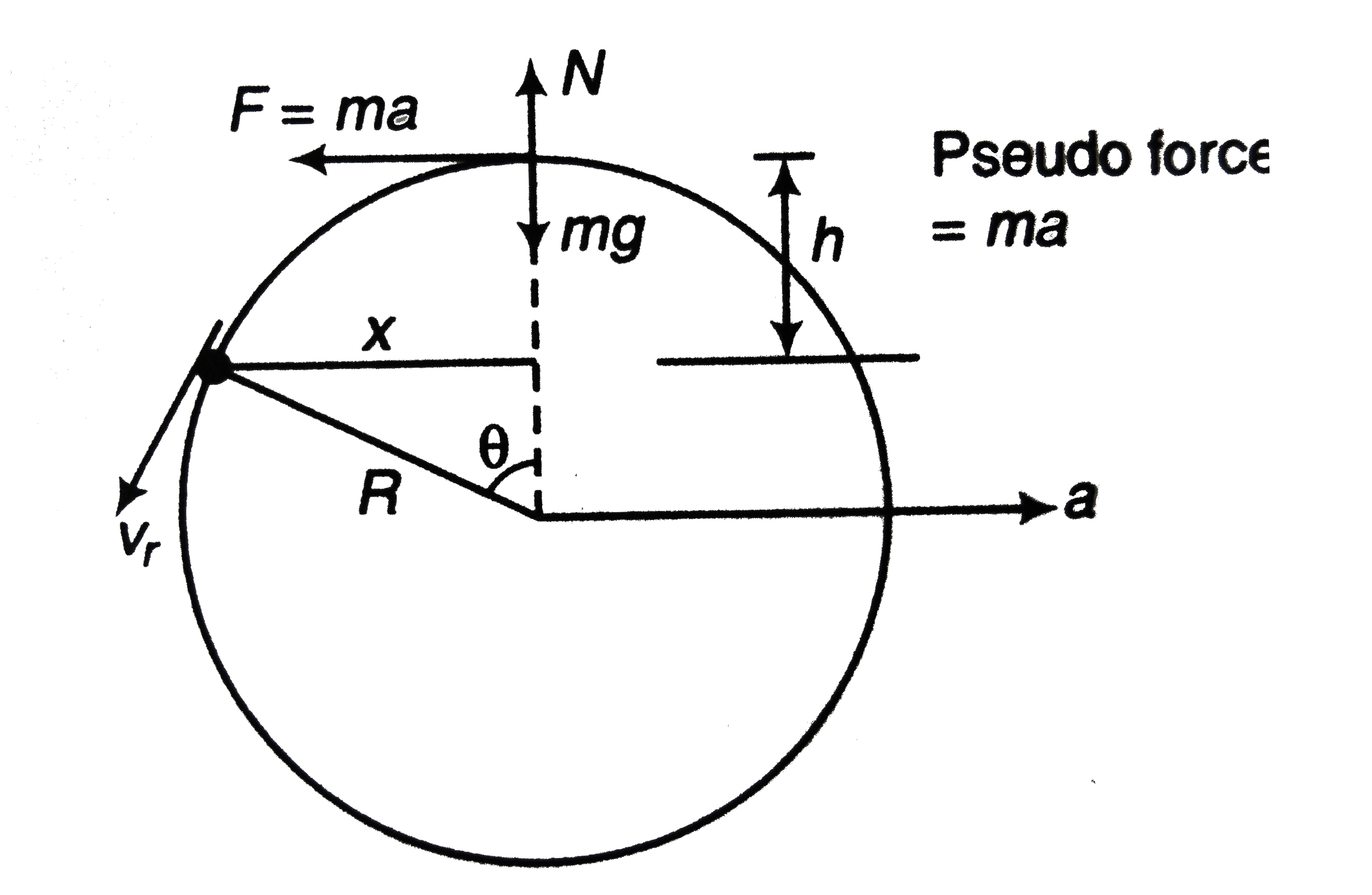
- A smooth spehre of radius R is made to translate oin a straight line w...
Text Solution
|
- A particle slides on the surface of a fixed smooth sphere starting fro...
Text Solution
|
- A smooth spehre of radius R is made to translate oin a straight line w...
Text Solution
|
- A particle rests on the top of a smooth hemisphere of radius r . It is...
Text Solution
|
- A small body A starts sliding off the top of a smooth sphere of radius...
Text Solution
|
- A smooth spehre of radius R is made to translate oin a straight line w...
Text Solution
|
- A smooth sphere of radius R is moving in a straight line with an accel...
Text Solution
|
- R त्रिज्या के एक स्थिर एंव चिकने गोले पर m द्रव्यमान का एक कण पकड़कर र...
Text Solution
|
- R त्रिज्या के एक स्थिर एंव चिकने गोले पर m द्रव्यमान का एक कण पकड़कर र...
Text Solution
|
 .
.