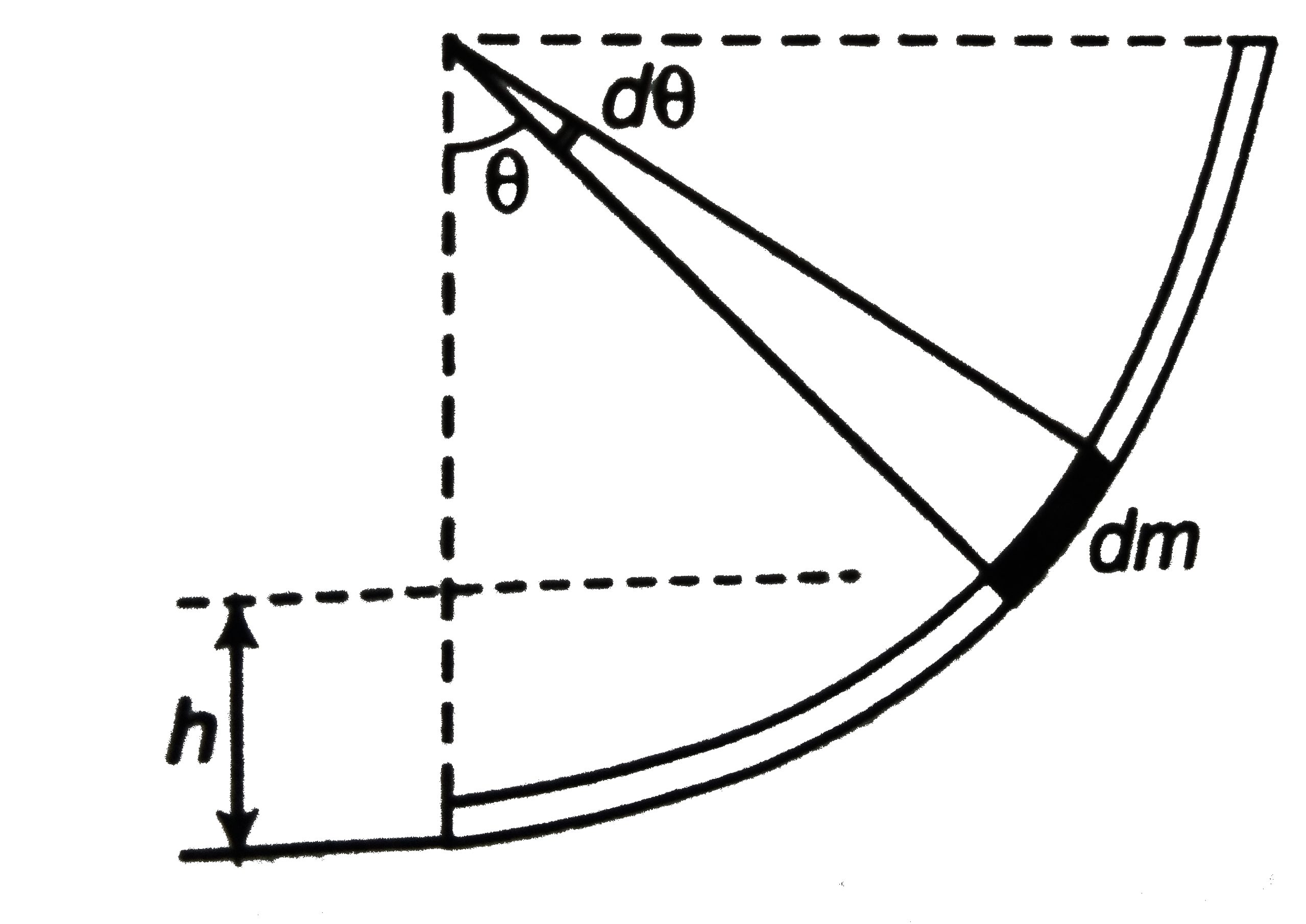
A
B
C
D
Text Solution
Verified by Experts
The correct Answer is:
Similar Questions
Explore conceptually related problems
Recommended Questions
- A smooth chain (AB) of mass (m) rests against a surface in the form of...
Text Solution
|
- A smooth chain (AB) of mass (m) rests against a surface in the form of...
Text Solution
|
- A block of mass m is placed at rest on a smooth wedge of mass M placed...
Text Solution
|
- A block of mass M with a semi - circular track of radius R rests on a ...
Text Solution
|
- Starting from rest, a particle rotates in a circle of radius R 2 m w...
Text Solution
|
- A tiny ball of mass m is released from the state of rest over a large ...
Text Solution
|
- A chain AB of length equal to the quarter of a circle of radius R is p...
Text Solution
|
- If a particle rotates along a circle of radius 3 m with an angular acc...
Text Solution
|
- A block is released at A and slides on smooth surface in shape of quar...
Text Solution
|