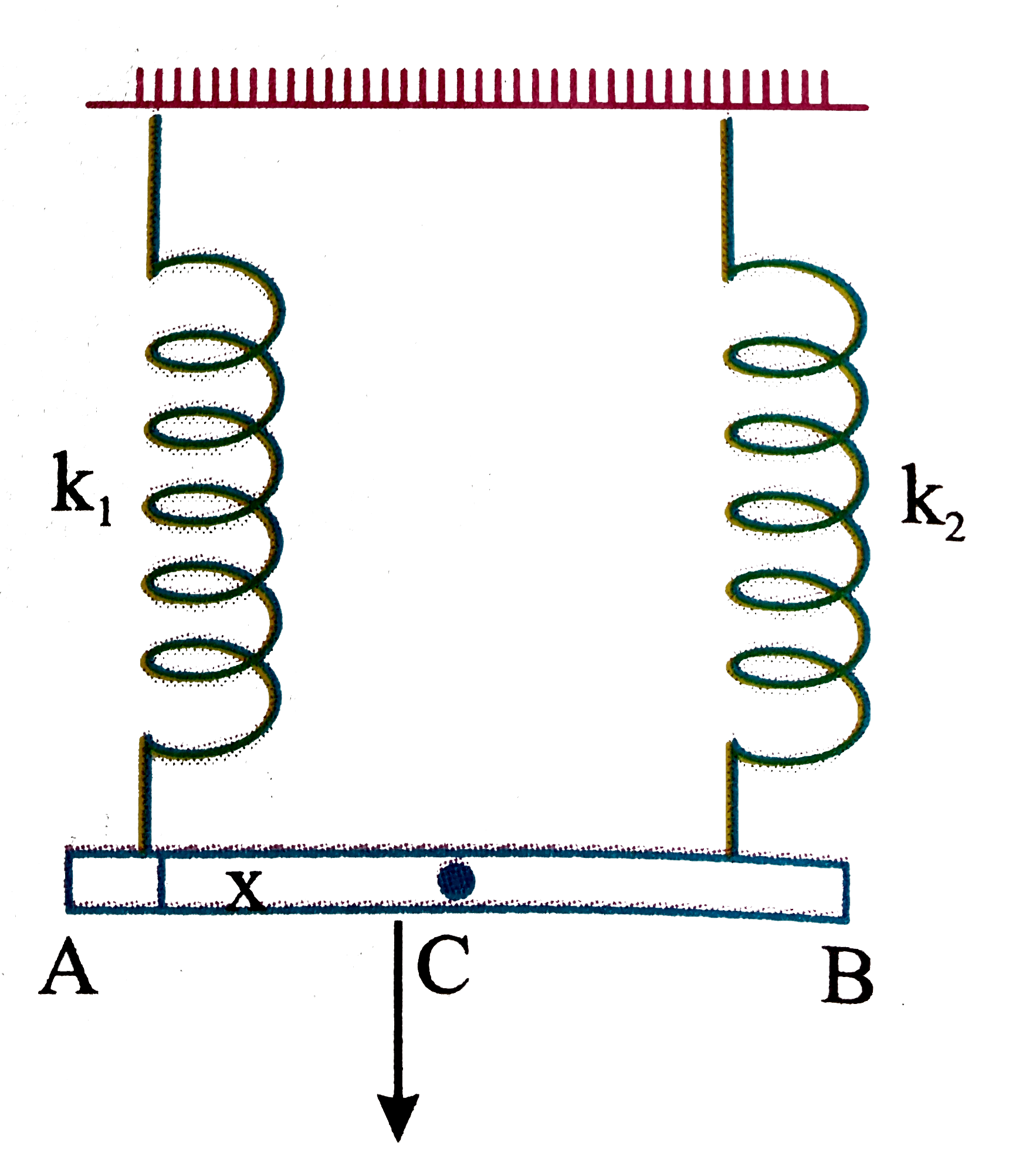
A
B
C
D
Text Solution
Verified by Experts
The correct Answer is:
Similar Questions
Explore conceptually related problems
Recommended Questions
- Two light vertical springs with equal natural length and spring consta...
Text Solution
|
- Two light springs of force constants (k1 and k2) and a block of mass (...
Text Solution
|
- Two light vertical springs with equal natural length and spring consta...
Text Solution
|
- In the figure a uniform rod of mass 'm' and length 'l' is hinged at on...
Text Solution
|
- A ring of mass m can slide over a smooth vertical rod. The ring is con...
Text Solution
|
- Two ideal springs of same make (the springs differ in their lengths on...
Text Solution
|
- Find the frequency of oscillations of the system in the figure. The ba...
Text Solution
|
- A rod of mass m and length l is connected by two spring of spring cons...
Text Solution
|
- A long uniform rod of length L, mass M is free to rotate in a horizont...
Text Solution
|