Home
Class 11
PHYSICS
A particle free to move along x-axis is ...

A particle free to move along x-axis is acted upon by a force `F=-ax+bx^(2) whrte a and b are positive constants. `For ximplies0`, the correct variation of potential energy function U(x) is best represented by.

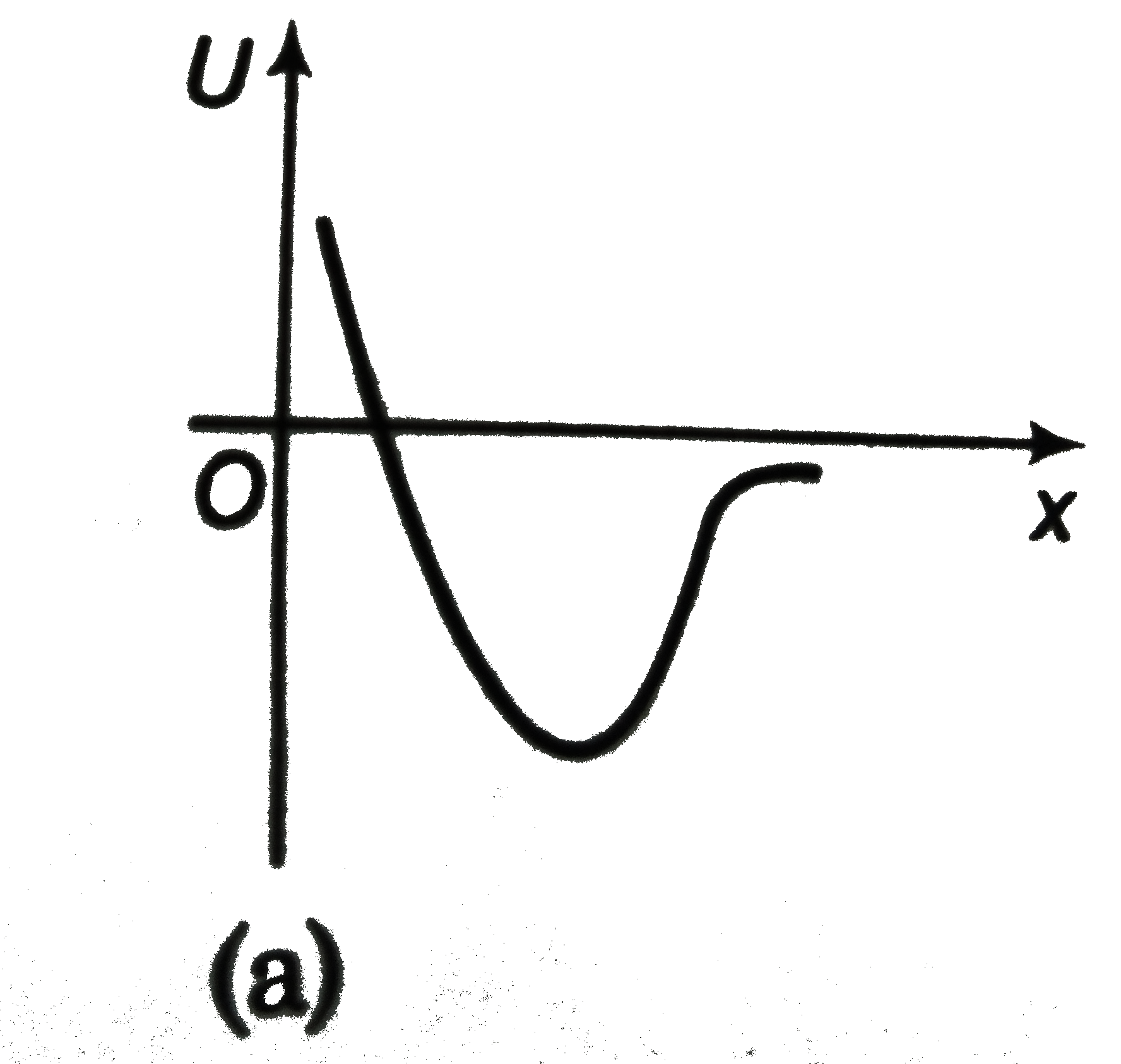
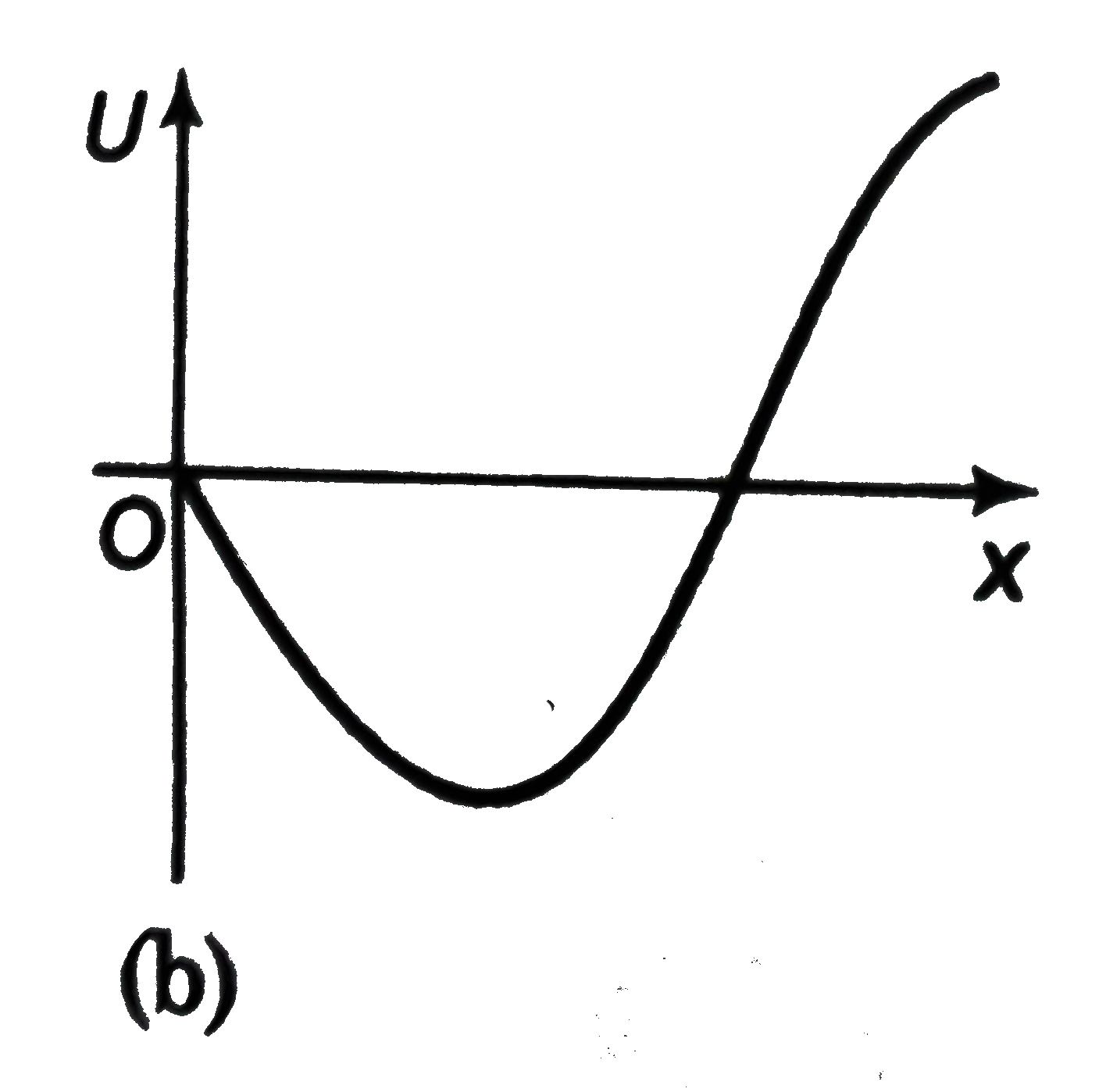
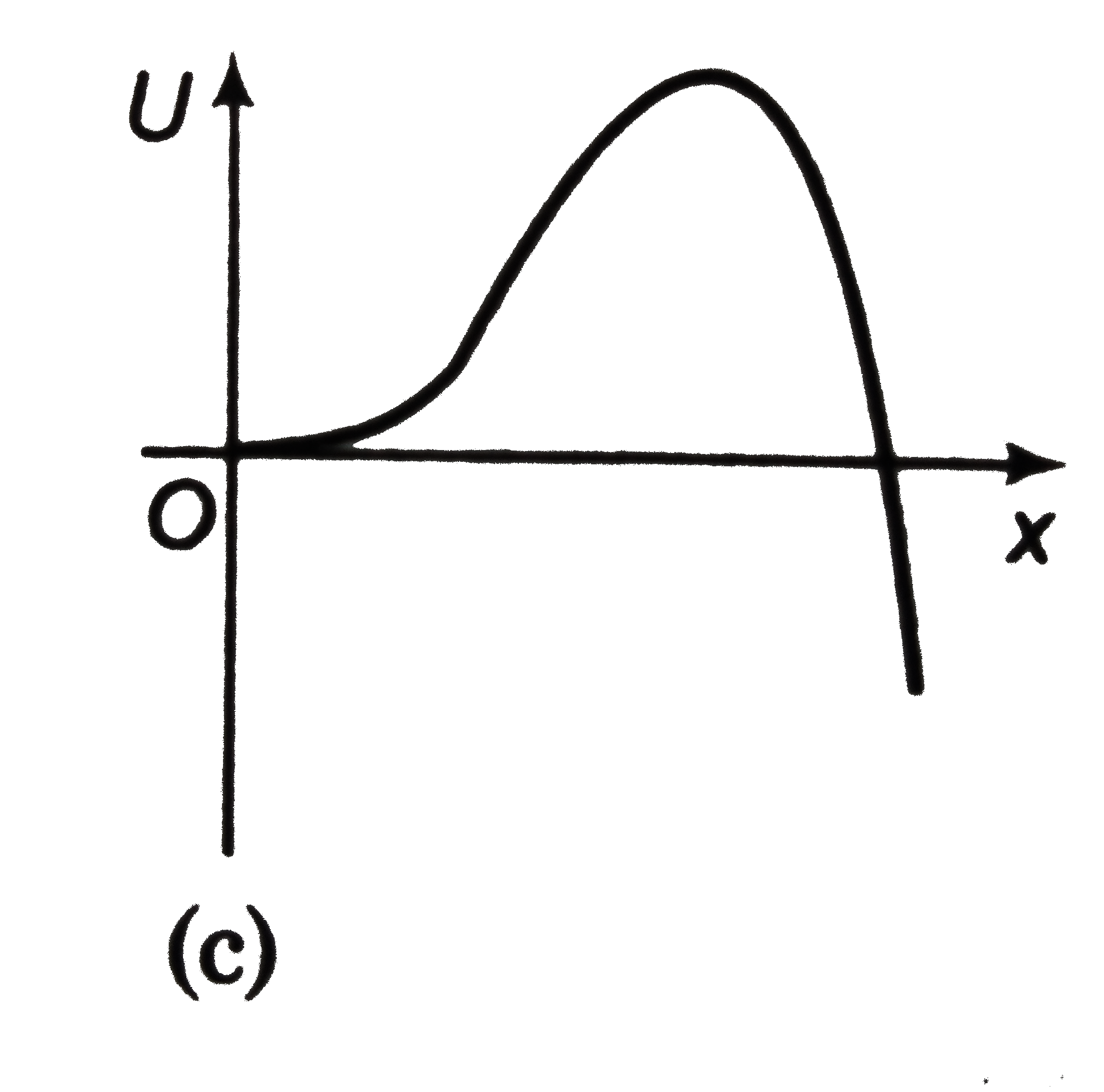
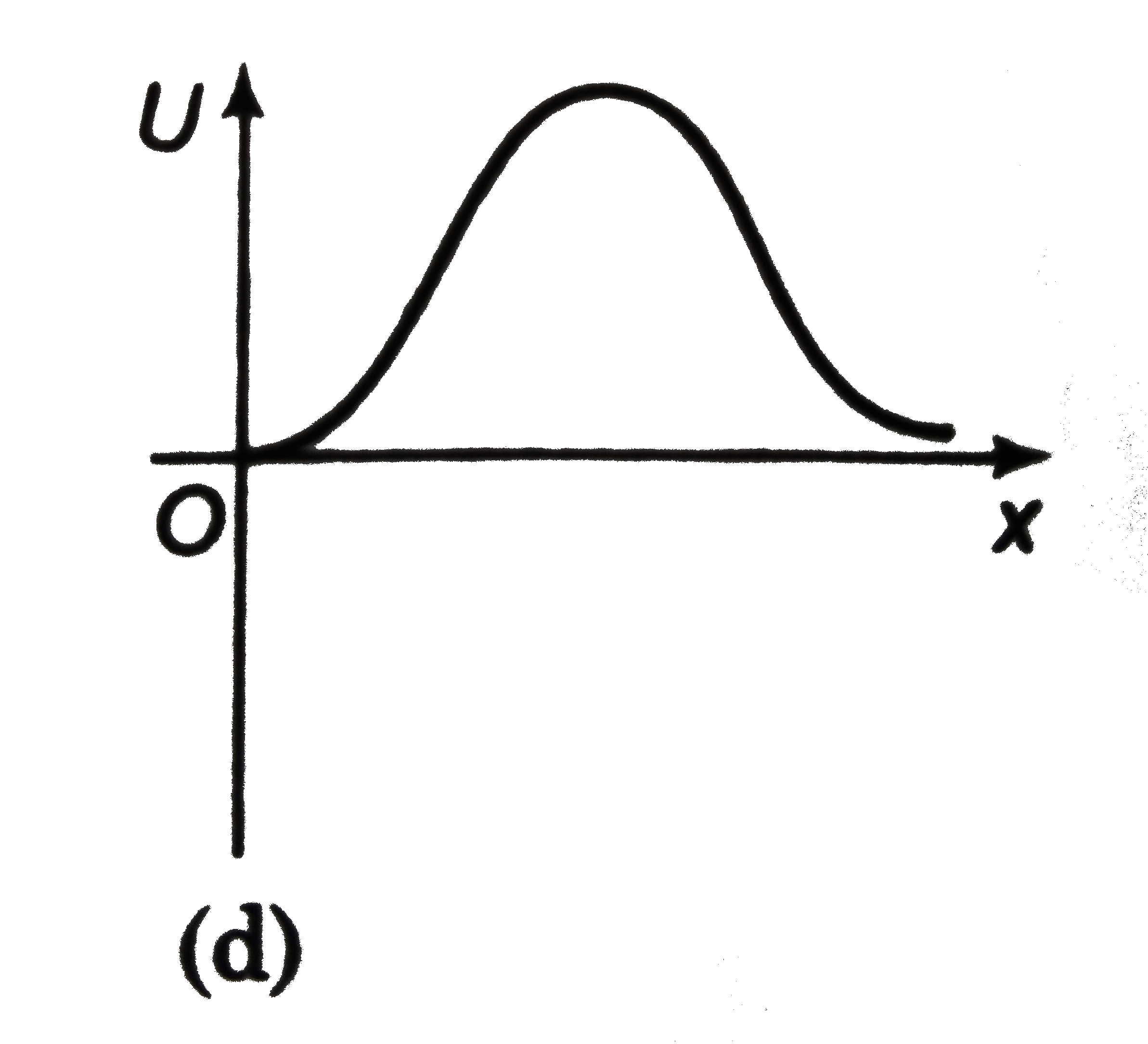
A

B

C

D

Text Solution

Verified by Experts

The correct Answer is:
C
`F =(dU)/(dx)` or `dU=-Fdx=(ax=bx^(2))dx`
Assuning `U=0` at `x=0`, and integrating the above equation we get,
`U = (ax^(2))/2-(bx^(3))/3`
`U-0` at `x=0` and `x=(3a)/(2b)`
For `xgt(3a)/(2b), bx^(3)/3gtax^(2)/2` and U will become negative. So, option (c) is the most approprite answer.
Promotional Banner

Similar Questions

Explore conceptually related problems

On a particle placed at origin a variable force F=-ax (where a is a positive constant) is applied. If U(0)=0, the graph between potential energy of particle U(x) and x is best represented by:-

A particle is acted upon by a force given by F = - alphax^(3) -betax^(4) where alpha and beta are positive constants. At the point x = 0, the particle is –

A particle, which is constrained to move along the x-axis, is subjected to a force from the origin as F(x) = -kx + ax^(3) . Here k and a are origin as F(x) = -kx + ax^(3) . Here k and a are positive constants. For x=0 , the functional form of the potential energy U(x) of particle is.

A particle of mass m moving along x-axis has a potential energy U(x)=a+bx^2 where a and b are positive constant. It will execute simple harmonic motion with a frequency determined by the value of

A particle moving along the x axis is acted upon by a single force F = F_0 e^(-kx) , where F_0 and k are constants. The particle is released from rest at x = 0. It will attain a maximum kinetic energy of :

A particle, which is constrained to move along x-axis, is subjected to a force in the some direction which varies with thedistance x of the particle from the origin an F (x) =-kx + ax^(3) . Here, k and a are positive constants. For x(ge0, the functional form of the potential energy (u) U of the U (x) the porticle is. (a) , (b) , (c) , (d) .

A particle is acted by x force F = Kx where K is a( + Ve) constant its potential mwrgy at x = 0 is zero . Which curve correctly represent the variation of putential energy of the block with repect to x