Text Solution
Verified by Experts
The correct Answer is:
Topper's Solved these Questions
CIRCULAR MOTION
DC PANDEY|Exercise Level 2 Single Correct|18 VideosCIRCULAR MOTION
DC PANDEY|Exercise Level 2 More Than One Correct|5 VideosCIRCULAR MOTION
DC PANDEY|Exercise Level 1 Objective|14 VideosCENTRE OF MASS, LINEAR MOMENTUM AND COLLISION
DC PANDEY|Exercise Level 2 Subjective|21 VideosCOMMUNICATION SYSTEM
DC PANDEY|Exercise Only One Option is Correct|27 Videos
Similar Questions
Explore conceptually related problems
DC PANDEY-CIRCULAR MOTION-Level 1 Subjective
- A car is travelling along a circular curve that has a radius of 50m . ...
Text Solution
|
- A 70kg man stands in contact against the inner wall of a hollw cylindr...
Text Solution
|
- A particle is projected with a speed u at angle theta with the horizon...
Text Solution
|
- Find the maximum speed at which a truck can safaly travel without topp...
Text Solution
|
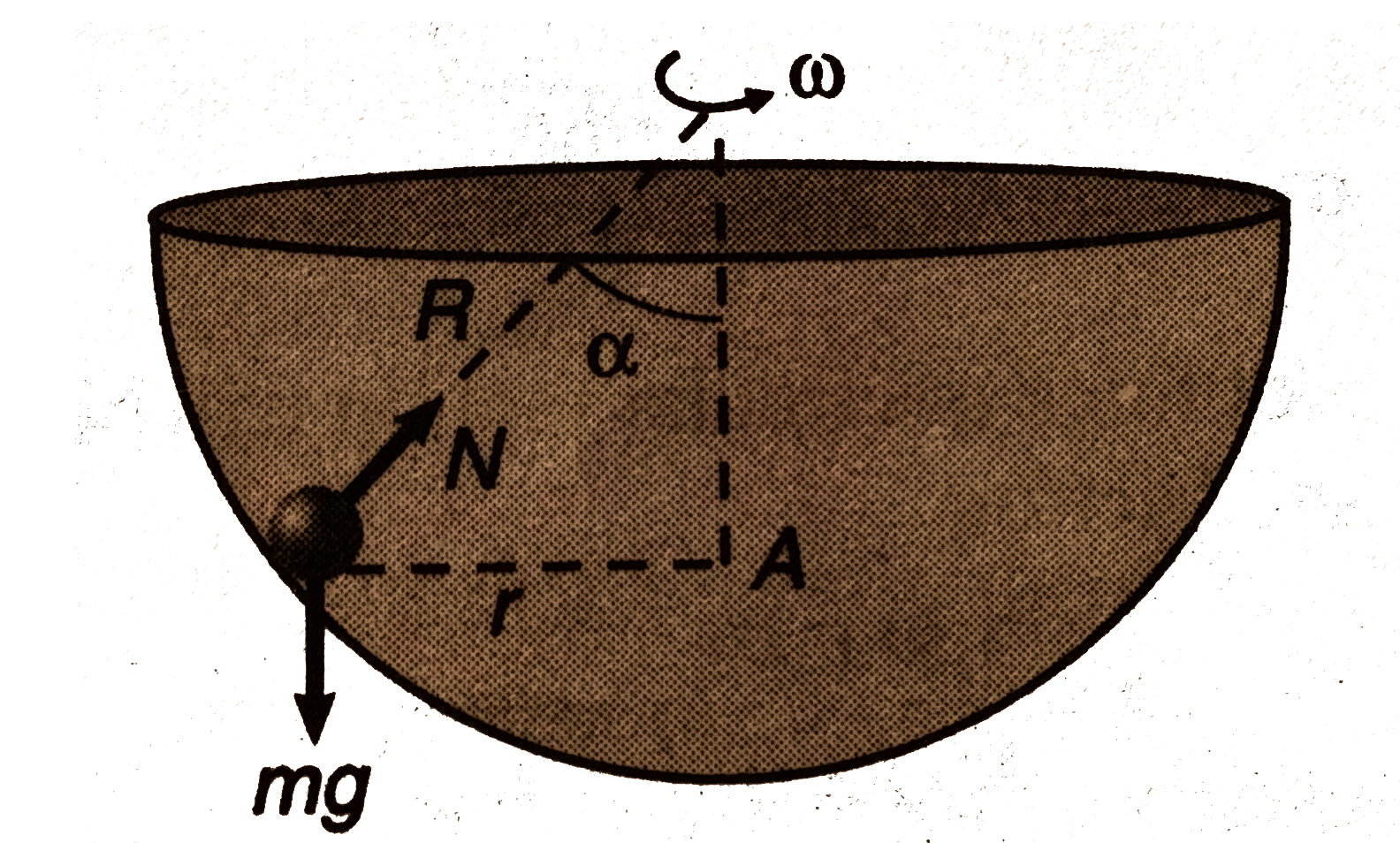
- A hemispherical bowl of radius R is set rotating about its axis of sym...
Text Solution
|
- Show that the angle made by the string with the vertical in a conical ...
Text Solution
|
- A boy whirls a stone of small mass in a horizontal circle of radius 1....
Text Solution
|
- A block of mass m is kept on a horizontal ruler. The frilction coeffic...
Text Solution
|
- A thin circular wire of radius R rotatites about its vertical diameter...
Text Solution
|
- Two block tied with a massless string of length 3m are placed on a rot...
Text Solution
|
- A small block slides with velocity 0.5sqrt(gr) on the horizontal frict...
Text Solution
|
- The bob of the pendulum shown in figure describes an are of in a verti...
Text Solution
|
- The sphere at A is given a downward velocity v(0) of magnitude 5m//s a...
Text Solution
|