Home
Class 11
PHYSICS
Three balls A, B and C are placed on a s...

Three balls A, B and C are placed on a smooth horizontal surface. Given that `m_A=m_C=4m_B`. Ball B collides with ball C with an initial velocity v as shown in figure. Find the total number of collisions between the balls. All collisions are elastic.

Text Solution

Verified by Experts

After first collision with `B+C`

`v_B^()'=((m-4m)/(m+4m))v=-3/5v`
`v_C^()'=((2xxm)/(m+4m))v=2/5v`
After second collision with `B+A`

Now since `9/25vlt2/5v` or `v_C`
So, B will not collide with C further,
Hence total collisions are only 2.
Promotional Banner

Topper's Solved these Questions

  • CENTRE OF MASS, LINEAR MOMENTUM AND COLLISION

    DC PANDEY|Exercise Level 1 Assertion and Reason|15 Videos

  • CENTRE OF MASS, LINEAR MOMENTUM AND COLLISION

    DC PANDEY|Exercise Level 1 Objective|42 Videos

  • CENTRE OF MASS, LINEAR MOMENTUM AND COLLISION

    DC PANDEY|Exercise Exercise 11.5|4 Videos

  • CENTRE OF MASS, IMPULSE AND MOMENTUM

    DC PANDEY|Exercise Comprehension type questions|15 Videos

  • CIRCULAR MOTION

    DC PANDEY|Exercise Medical entrances s gallery|19 Videos

Similar Questions

Explore conceptually related problems

Three balls A, B and C(m_(A)=m_(C)=4m_(B)) are placed onn a smooth horizontal surface. Ball B collides with ball C with an initial velocity v as shown in figure. Find the total number of collision betwenent the balls (all collisions are elastic).

A ball A of mass M collides elastically with a similar ball B at rest as shown in figure. Initially velocity of ball A is u m/s. After collision,

Two balls marked 1 and 2 of the same mass m and a third ball marked 3 of mass M are arranged over a smooth horizontal surface as shown in the figure. Ball 1 moves with a velocity v_(1) towards ball 2. All collisions are assumed to be elastic. If Mltm , the number of collisions between the balls will be.

N identical balls are placed on a smooth horizontal surface. An another ball of same mass collides elastically with velocity u with first ball of N balls. A process of collision is thus started in which first ball collides with second ball and the with the third ball and so on. The coefficient of restitution for each collision is e . Find the speed of Nth ball.

Three identical balls 1, 2 and 3 are placed together at rest on a smooth horizontal surface. A fourth identical ball moving with velocity u in line of first three balls collides head on elastically as shown in figure, then

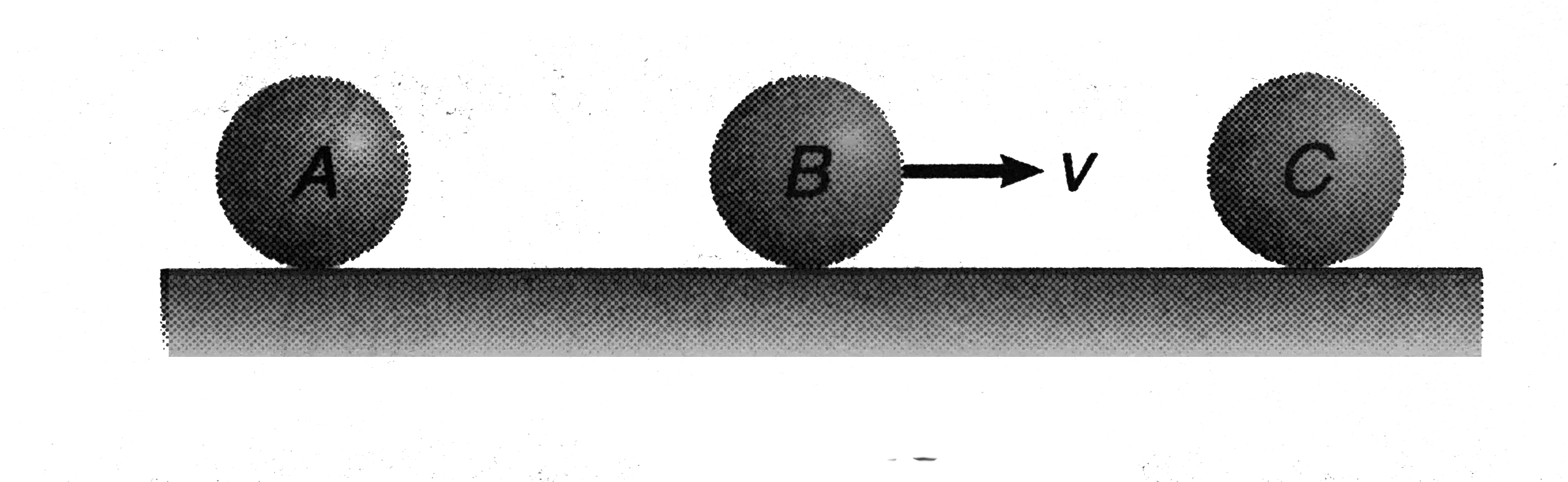
Three balls A, B and C of same mass m are placed on a frictionless horizontal plane in a straight line as shown. Ball A is moved with velocity u towards the middle ball B . If all the collisions are elastic, find the final velocities of all the balls.

Two balls each of mass 'm' are moving with same velocity v on a smooth surface as shown in figure. If all collisions between the balls and balls with the wall are perfectly elastic, the possible number of collisions between the balls and wall together is

A ball A of mass 3 m is placed at a distance d from the wall on a smooth horizontal surface Another ball B of mass m moving with velocity u collides with ball A . The coefficient of restitution between the balls and the wall and between the balls is e (a) the velocity of ball B after collision is (u(3e-1))/(4) . (b) the velocity of ball B after collision is (u(2e-1))/(4) . ( c) after collision, ball A will have away by distance (d(2e-1))/((2e-1)) during the time ball B returns back to wall. (d) after collision, ball A will move away by distance (d(e-1))/((3e-1)) during the time ball B returns back to wall.

A ball moving with speed v collides with a horizontal smooth surface at an angle theta with normal to surface as shown in figure. If coefficient of restitution of collision is e, then find v'