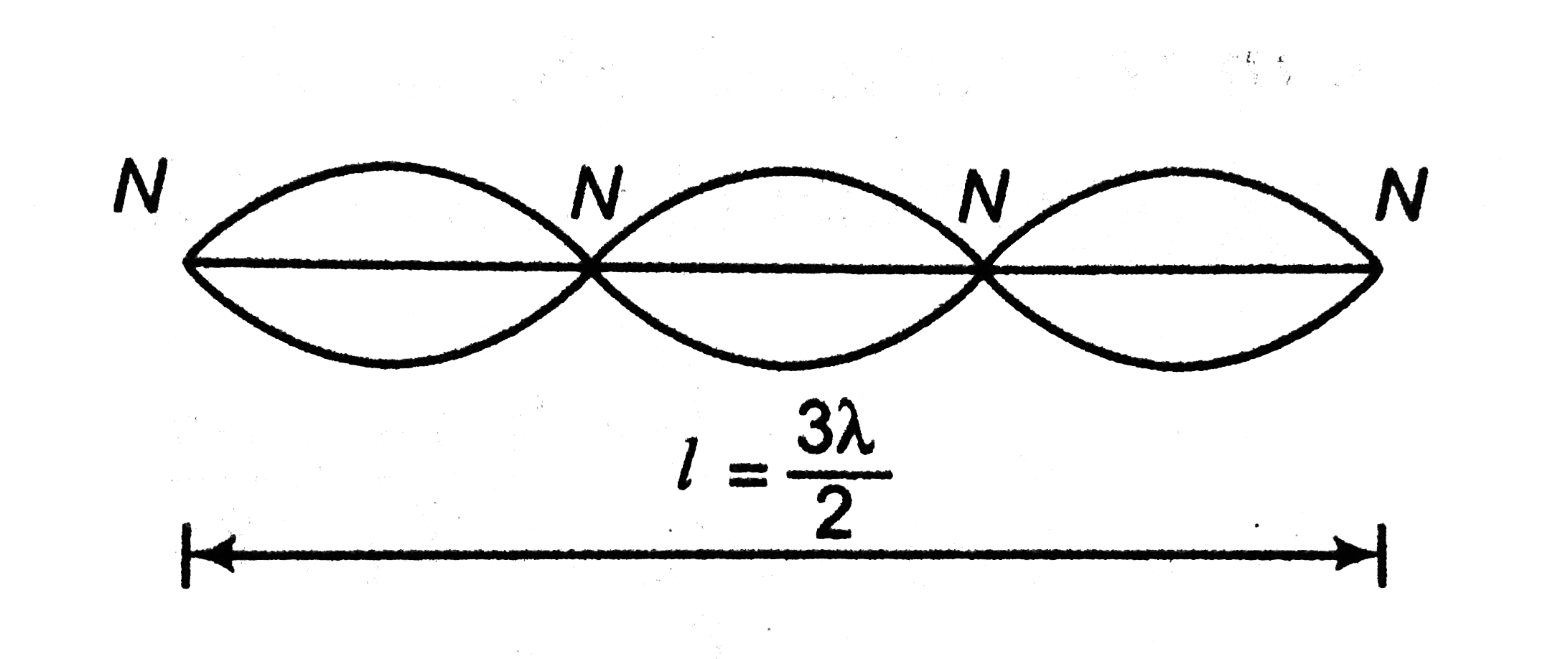
Text Solution
Verified by Experts
The correct Answer is:
Similar Questions
Explore conceptually related problems
Recommended Questions
- A string of linear mass density 5.0 xx 10^-3 kg//m is stretched under ...
Text Solution
|
- A string of linear mass density 5.0 xx 10^-3 kg//m is stretched under ...
Text Solution
|
- A wire stretched between two rigid supports vibrates in its fundamenta...
Text Solution
|
- A wire stretched between two rigid supports vibrates in its fundamenta...
Text Solution
|
- A string is vibrating in its fifth overtone between two rigid supports...
Text Solution
|
- A wire stretched between two rigid supports vibraes in its fundamental...
Text Solution
|
- A wire stretched between two rigid supports vibrates in its fundamenta...
Text Solution
|
- A streched string is vibrating in the second overtone , then the numbe...
Text Solution
|
- The mass of a string is 5.0 xx 10^(-3) kg, and it is stretched so that...
Text Solution
|