Home
Class 11
PHYSICS
Three waves due to three coherent source...

Three waves due to three coherent sources meet at one point. Their amplitudes are `sqrt2A_0 , 3A_0` and `sqrt2A_0` . Intensity corresponding to `A_0` is `l_0`. Phasse difference between first and second is `45^@`. Path difference between first and third is `lambda/4`. In phase angle, first wave lags behind from the other two waves. Find resultant intensity at this point.

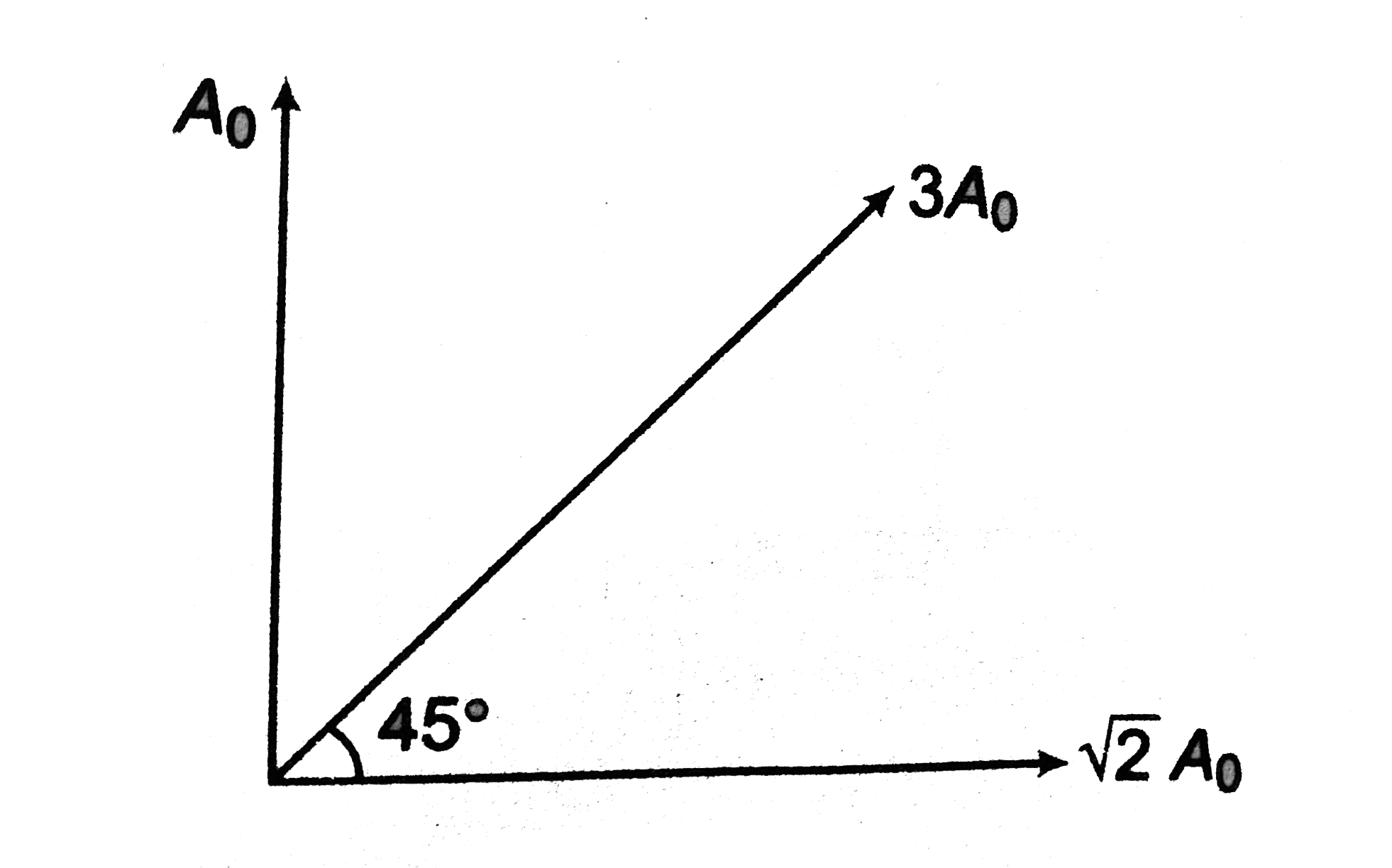
Text Solution

Verified by Experts

The correct Answer is:
B
Path difference of `lambda/4` is equivalent to a phase
difference of `pi/2`.

`A_("net") = 5A_0`
`I prop A^2`
`rArr I_(net) = 25 I_0`
Promotional Banner

Topper's Solved these Questions

  • SUPERPOSITION OF WAVES

    DC PANDEY|Exercise Exercise 18.2|4 Videos

  • SUPERPOSITION OF WAVES

    DC PANDEY|Exercise Exercise 18.3|5 Videos

  • SUPERPOSITION OF WAVES

    DC PANDEY|Exercise miscellaneous example|7 Videos

  • SOUND WAVES

    DC PANDEY|Exercise Exercise 19.7|4 Videos

  • THERMOMETRY THERMAL EXPANSION AND KINETIC THEORY OF GASES

    DC PANDEY|Exercise Medical entrance gallary|30 Videos

Similar Questions

Explore conceptually related problems

Three waves from three coherent sources meet at some point. Resultant amplitude of each is A_0 . Intensity corresponding to A_0 is I_0 . Phase difference between first wave and second wave is 60^@ . Path difference between first wave and third wave is lambda/3 . The first wave lags behind in phase angle from second and third wave. Find resultant intensity at this point.

Three waves from three coherent sources meet at some point . Resultant amplitude of each is A_0 . Intensity corresponding to A_0 is I_0 . Phase difference between first wave and the second wave is 60^@ . Path difference between first wave and the third wave is lambda/3. The first wave lags behind in phase angle from second and the third wave. Find resultant intensity at this point.

In interference, two individual amplitudes are A_0 each and the intensity is I_0 each. Find resultant amplitude and intensity at a point, where: (a) phase difference between two waves is 60^@ . (b) path difference between two waves is lambda/3 .

In interference, two individual amplitudes are A_(0) each and the intensity is I_(0) each. Find resultant amplitude and intensity at a point, where (a) phase difference between two waves is 60^(@) . (b) path difference between two waves is lambda/3 .

Maximum intensity in YDSE is I_0 . Find the intensity at a point on the screen where (a) The phase difference between the two interfering beams is pi/3. (b) the path difference between them is lambda/4 .

Light waves of wavelength 5460 A, emitted by two coherent sources, meet at a point after travelling different paths. The path difference between the two wave trains at that point is 2.1 mum . then phase difference will be ?

The path difference between two interfering waves of equal intensities at a point on the screen is lambda//4 . The ratio of intensity at this point and that at the central fringe will be

Phase difference between two waves having same frequency (v) and same amplitude (A) is 2pi//3 . If these waves superimpose each other, then resultant amplitude will be–

Light waves from two coherent source arrive at two points on a screen with path difference 0 and lambda//2 . Find the ratio of intensities at the points.