Home
Class 11
PHYSICS
In a stationary wave that forms as a res...

In a stationary wave that forms as a result of reflection of waves from an obstacle, the ratio of the amplitude at an antinode to the amplitude at node is 6. What percentage of energy is transmitted?

Text Solution

Verified by Experts

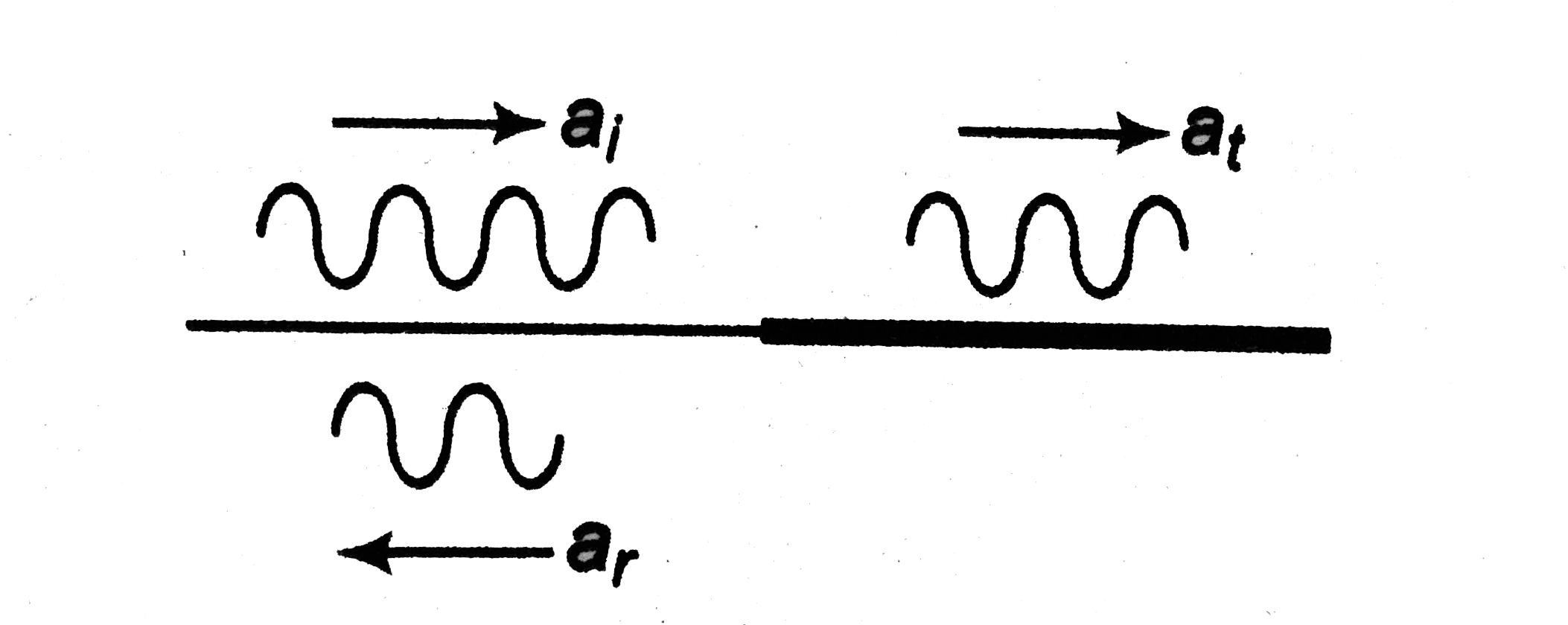
The correct Answer is:
D
Let `a_i and a_r` be the amplitudes of incident and
reflected waves.

Then,
`(a_i + a_r)/(a_i-a_r) = 6`
Hence, `a_r/a_i = 5/7`
Now, `E_r/E_i = (a_r/a_i)^2 = (5/7)^2 `
= 0.51
or percentage of energy reflected is
`100 xx (E_r /E_i) = 51%`
So, percentage of energy transmitted will be
`(100 - 51)%` or `49 % ` .
Promotional Banner

Topper's Solved these Questions

  • SUPERPOSITION OF WAVES

    DC PANDEY|Exercise Level 2 Comprehension Based|3 Videos

  • SOUND WAVES

    DC PANDEY|Exercise Exercise 19.7|4 Videos

  • THERMOMETRY THERMAL EXPANSION AND KINETIC THEORY OF GASES

    DC PANDEY|Exercise Medical entrance gallary|30 Videos

Similar Questions

Explore conceptually related problems

In a stationary wave that forms as a result of reflection of wave from an obstacle, the ratio of this amplitude at an antinode to the amplitude at anode is n. The friction of energy reflected is

In a stationary wave pattern that forms as a result of reflection pf waves from an obstacle the ratio of the amplitude at an antinode and a node is beta = 1.5. What percentage of the energy passes across the obstacle ?

A harmonic source (S) is driving a taut string. The other end of the string is tied to a wall that is not so rigid. It is observed that standing waves are formed in the string with ratio of amplitudes at the antinodes to that at the nodes equal to 8. What percentage of wave energy is transmitted to the wall?

In a stationary waves, the amplitude of vibrating paticles

The amplitude of a stationary waves is

The ratio of intensities of two waves is 9 : 25. What is the ratio of their amplitude ?

Stationary waves are produced in a length of wire fixed between two points . Compare the amplitudes at an antinode for the fundamental and the first overtone . Assume that the total energy of the initial waves is , on an average , equally divided between the two modes.