Home
Class 12
PHYSICS
A charged particle (q,m) enters uniform...

A charged particle `(q,m)` enters uniform magnetic field B at angle `alpha` shown in figure with speed `v_0`. Find

a. The angle `beta` at which it leves the magnetic field
b. time spent by the particle in magnetic field and
c. the distance `C`.

Text Solution

Verified by Experts

a. Here, velocity of the particle is in the plane of paper while the magnetic field is perpendicular to the paper inwards, i.e. angle between v and B is `90^@`. So the path is a circle. The radius of the circle is `r=(mv_0)/(Bq)`

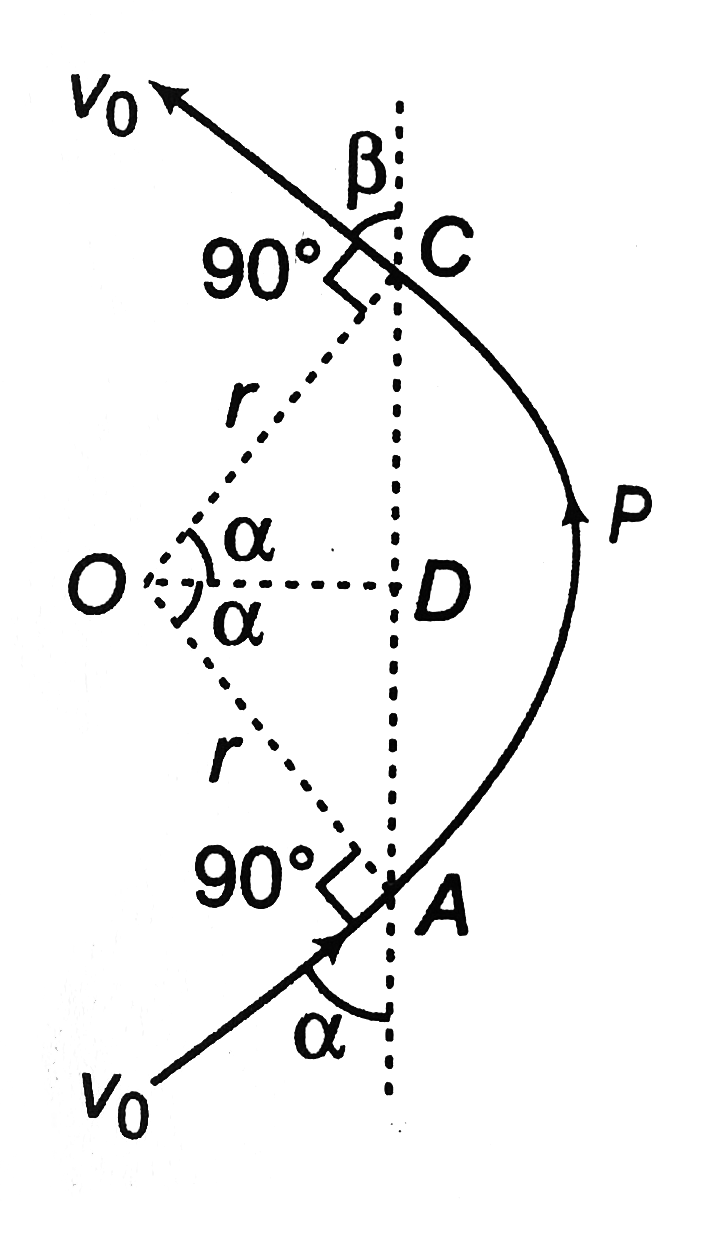
`O` is the centre of the circle. In `/_\AOC`
`/_OCD=/_OAD`
`or 90^@-beta=90^@-alpha`
`:. beta=alpha`
b. `/_COD=/_DOA=alpha` (as `/_OCD=/_OAD=90^@-alpha)`
`:. /_AOC=2alpha`
or length `APC=r(2alpha)=(2mv_0)/(Bq) .alpha`
`:. t_(APC)=(APC)/v_0=(2malpha)/(Bq)`
Alternate method
`t_(APC)=(T/(2pi))(2alpha)=(alpha/pi).T`
`=(alpha/pi)((2pim)/(Bq))=(2alpham)/(Bq)`
c. Distance `AC=2 (AD)=2(rsinalpha)`
`=(2mv_0)/(Bq)sinalpha`
Promotional Banner

Topper's Solved these Questions

  • MAGNETICS

    DC PANDEY|Exercise Exercise|160 Videos

  • MAGNETICS

    DC PANDEY|Exercise INTRODUCTORY EXERCISE|1 Videos

  • MAGNETIC FIELD AND FORCES

    DC PANDEY|Exercise Medical entrance s gallery|59 Videos

  • MAGNETISM AND MATTER

    DC PANDEY|Exercise Medical gallery|1 Videos

Similar Questions

Explore conceptually related problems

When a charged particle enters a uniform magnetic field its kinetic energy

A charged particle enters a uniform magnetic field perpendicular to it. The magnetic field

A charged particle enters into a uniform magnetic field the parameter that remains constant is

A charged particle (q, m) enters perpendicular in a uniform magnetic field B and comes out field as shown. The angle of deviation theta time taken by particle to cross magnetic field will be

A particle of mass m and charge +q enters a region of magnetic field with a velocity v, as shown in Fig. 1.93. a. Find the angle subtended by the circular arc described by it in the magnetic field. b. How long does the particle stay inside the magnetic field? c. If the particle enters at E, what is the intercept EF?

A charged particle entering a magnetic field from outside in a direction perpendicular to the field

A charged particle enters a region of uniform magnetic field at an angle of 85@ to the magnetic line of force . The path of the particle is a circle .

Four particles enter a region of uniform magnetic field. Their trajectories are shown in figure. What are the signs of the charge of all four particles ?