Home
Class 12
PHYSICS
An electron gun G emits electons of ener...

An electron gun `G` emits electons of energy `2 keV` travelling in the positive x-direction. The electons are required to hit the spot `S` where `GS=0.1 m`, and the line `GS` makes an angle of `60^@` with the x-axis as shown in figure. A uniform magnetic field `B` parallel to `GS` exists in the region outside the electron gun.

find the minimum value of `B` needed to make the electrons hit `S`.

Text Solution

Verified by Experts

Kinetic energy of electron
`K=1/2mv^2=2keV`
`:.` Speed of electron `v=sqrt((2K)/m)`
`v=sqrt((2xx2x1.6xx10^-16)/(9.1xx10^-31))m/s`

`=2.65xx10^7m/s`
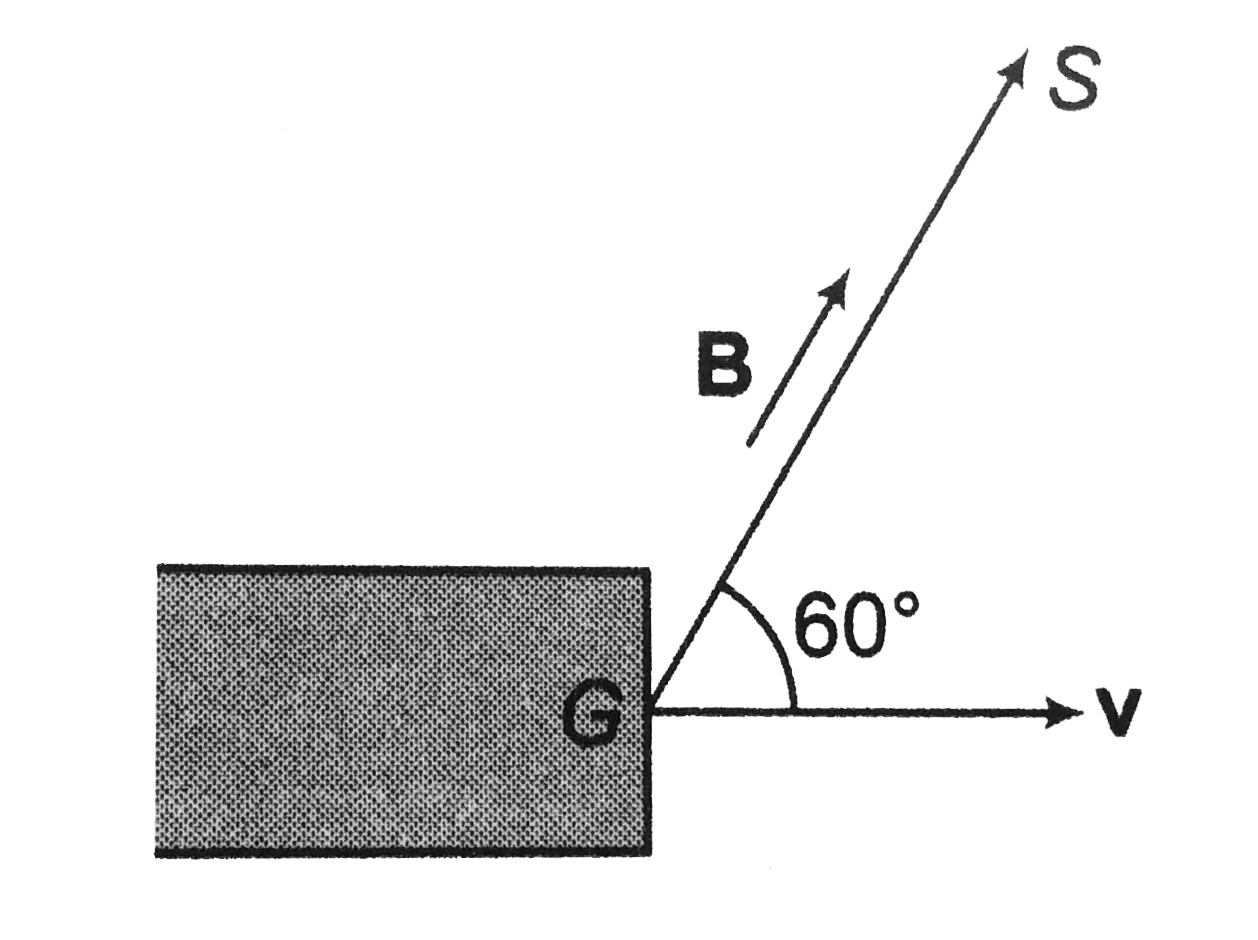
Since the velocity v of the electron makes an angle of `theta=60^@` with ethe magnetic field `B`, the path will be a helix. So, the particle will hit `S` if
`GS=np`
Here `n=1,2,3.........`
`p=pitch of helix =(2pim)/(qB) vcostheta`
But for to be minimum `n=1`
Hence, `GS=P=(2pim)/(qB) vcostheta`
`B=B_(min)=(2pimvcostheta)/(q(GS)`
Substituting the values we have
`B_(min)=((2pi)(9.1xx10^-31)(2.65xx10^7)(1/2))/((1.6xx10^-19)90.1)`
or `B_(min)=(4.73xx10^-3T)`
Promotional Banner

Topper's Solved these Questions

  • MAGNETICS

    DC PANDEY|Exercise Exercise|160 Videos

  • MAGNETICS

    DC PANDEY|Exercise INTRODUCTORY EXERCISE|1 Videos

  • MAGNETIC FIELD AND FORCES

    DC PANDEY|Exercise Medical entrance s gallery|59 Videos

  • MAGNETISM AND MATTER

    DC PANDEY|Exercise Medical gallery|1 Videos

Similar Questions

Explore conceptually related problems

An electron gun G emits electron of energy 2kev traveling in the positive x -direction.The electrons are required to hit the spot S where GS=0.1 m and the line GS makes an angle of 60^(@) with the x -axis, as shown in the fig.A uniform magnetic field vecB parallel to GS exists in the region outside of electron gun.Find the minimum value of B needed to make the electron hit S .[Take mass of electron =9xx10^(-31)kg ]

An electron gun G emits electrons of energy 2ke V travelling in the positive x- direction . The electrons are required to hit the spot S where GS = 0.1m , and the line GS makes an angle of 60^(@) with the x-axis as shown in the fig. A uniform magnetic field vec(B) parallel to GS exists in the region outside the electron gun. Find the GS exists in the region outside the electron gun. Find the minimum value of B needle to make the electron hit S .

A uniform electric field and a uniform magnetic field are acting along the same direction in a certain region. If an electron is projected in the same direction then the electron

One electron gun is firing electrons with a speed V as shown in the figure. There is a target P which is to be hit. Electrons emerge from point 0 and line OP makes an angle with the direction of velocity of electrons. The length of OP is L.A uniform magnetic field B is applied parallel to line OP. Charge on the electron ise and the mass of electrons is m. What minimum magnetic field is needed so that electrons may hit the target P?

In vacuum an electron of energy 10 keV hits tungsten target, then emitted radiation will be

A uniform electric field and a uniform magneitc field exist in a region in the same direction An electron is projected with velocity pointed in the same direction the electron will

Find the equation of the line which passes through the point (3,-4) and makes an angle of 60^(@) with the positive direction of x - axis ?