Home
Class 12
PHYSICS
Two long straight parallel wieres are 2m...

Two long straight parallel wieres are `2m` apart, perpendicular to the plane of the paper. The wire A carries a current of `9.6 A`, directed into the plane of the paper. The wire `B` carries a current such that the magnetic field of induction at the point `P`, at a distance of `10/11` m from the wire B, is zero. find
a. the magnitude and directiion of the current in B.
b. the magnitude of the magnetic field of induction of the pont `S`.
c. the force per unit length on the wire `B`.

Text Solution

Verified by Experts

a. Direction of current at `B` should be perpendicular to paper outwards. Let curent in this wire be `i_B`. Then
`mu_0/(2pi) i_A/((2+10/11))=mu_0/(2pi) i_B/((10/11))`
or `i_B/i_A=10/32`
or `i_B=10/32xxi_A=10/32x9.6=3A`
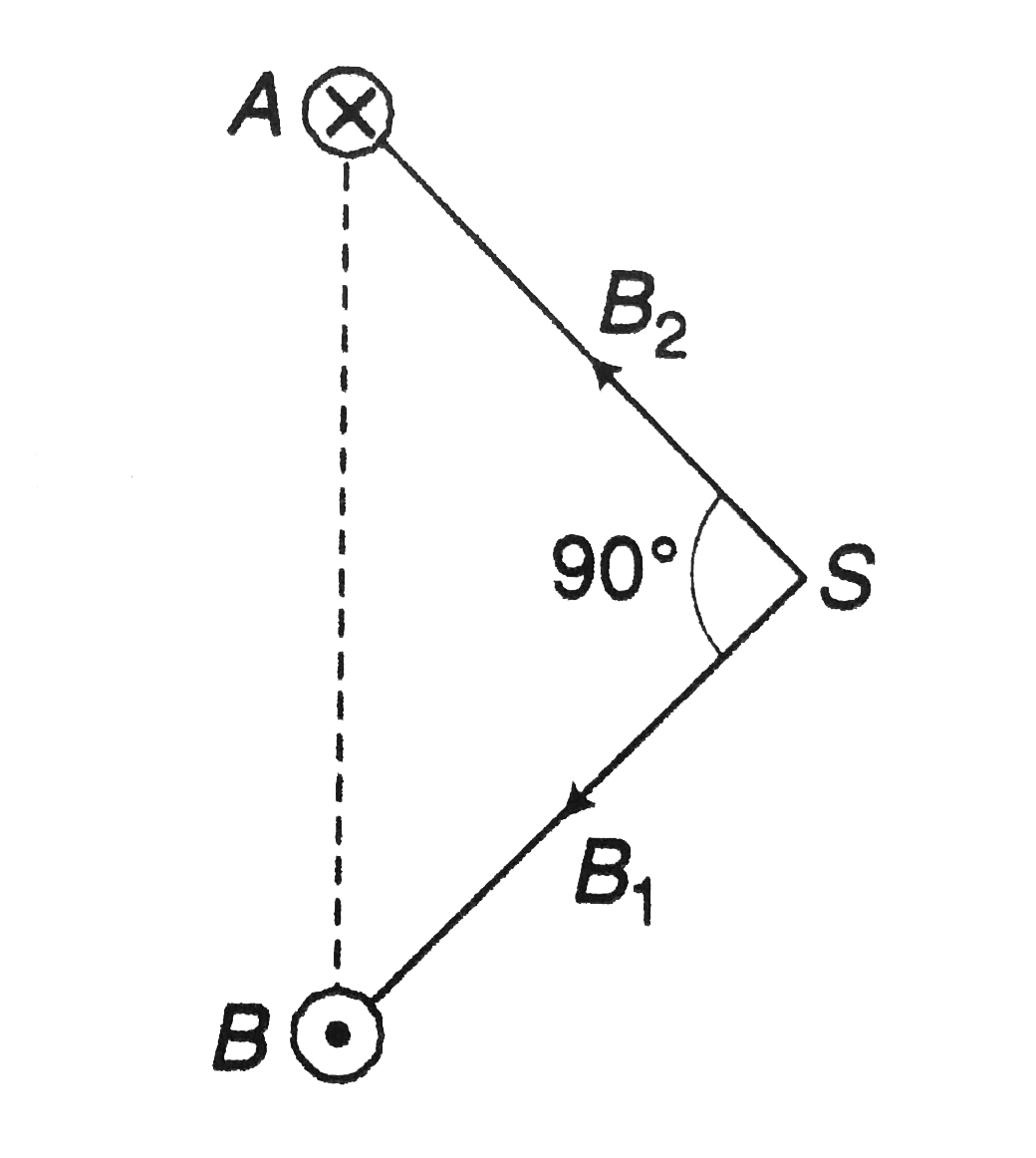
b. Since `AS^2+BS^2+AB^2`
`/_ASB=90^@`
At `S:B_1=` Magnetic field due to `i_A`
`=mu_0/(2pi) i_A/1.6=((2xx10^I-7)(9.6))/1.6`
`=12xx10^-7T`
`B_2=`magnetic field to due to `i_B`
`=mu_0/(2pi) i_B/1.2`
`=((2xx10^i-7)(3))/1.2`
`=5xx10^-7T`
Since `B_1 and B_2` are mutually perpedicular.Net magnetic field at S would be
`b=sqrt(B_1^2+B_2^2)`
`=sqrt((12xx106i-7)^2+(5xx10^-7)^2)`
`=13xx10^-7T`
c. Force per unit length on wire B:
`F/l=mu_0/(2pi)(i_Ai_B)/r` `[:.r=AB=2m]`
`=((2xx10^-7)(9.6xx3))/2`
`=2.88xx10^I-6N/m`
Promotional Banner

Topper's Solved these Questions

  • MAGNETICS

    DC PANDEY|Exercise Exercise|160 Videos

  • MAGNETICS

    DC PANDEY|Exercise INTRODUCTORY EXERCISE|1 Videos

  • MAGNETIC FIELD AND FORCES

    DC PANDEY|Exercise Medical entrance s gallery|59 Videos

  • MAGNETISM AND MATTER

    DC PANDEY|Exercise Medical gallery|1 Videos

Similar Questions

Explore conceptually related problems

Two long, straight wires a and b are 2*0 m apart, perpendicular to the plane of the paper as shown in figure . The wire a carries a current of 9*6 A directed into the plane of the figure,The magnetic field at the point P at a distance of 10/11 m from the wire b is zero. Find (a) the magnitude and direction of the current in b, (b) the magnitude of the magnetic field B at the point s and (c) the force per unit length on the wire b .

Two long, straight, parallel wires are 1.00m apart (as shown in Fig). The upper wire carries a current I_1 of 6.00A into the plane of the paper. What is the magnitude of the net field at Q?

Two long, straight, parallel wires are 1.00m apart (as shown in Fig). The upper wire carries a current I_1 of 6.00A into the plane of the paper. What is the magnitude of the net field at S?

Two long, straight, parallel wires are 1.00m apart (as shown in Fig). The upper wire carries a current I_1 of 6.00A into the plane of the paper. What must the magnitude of the current I_2 be for the net field at point P to be zero?

Two long parallel wires P and Q are both perpendicular to the plane of the paper with distance 5m between them. If P and Q carry current of 2.5 amp and 5 amp respectively in the same direction, then the magnetic field at a point half way between the wires is

Two long parallel wire A and B situated perpendicuilar to the plane of the paper at a distance 2a are carrying equal currents I in opposite direction as show in the figure . The value of magnetic induction at point P situated at equal distance r from both the wires will be

A long straight wire carries a current of 35A . What is the magnetic of the field vecB at a point 20cm from the wire?

Find the magnitude and direction of magnetic field at point P due to the current carrying wire as shown in

Two infinitely long straight parallel wire are 5 m apart, perpendicular to the plane of paper. One of the wires, as it passes perpendicular to the plane of paper, intersects it at A and carries current I in the downward direction. The other wire intersects the plane of paper at point B and carries current k int the outward direction O in the plane of paper as shown in Fig. With x and y axis shown, magnetic induction at O in the component form can be expressed as