Home
Class 12
PHYSICS
A wire loop carrying a current I is plac...

A wire loop carrying a current `I` is placed in the `xy`-plane as shown in figure

a. If a particle chsarge +Q and mass m is placed at in centre `P` and given a velocity `v` along `NP` (see figure), find its instaneous acceleration.
If an external uniform magnetic induction field `B=Bhati` is applied, find the force and the torque acting on the loop due to this field.

Text Solution

Verified by Experts

a. Magnetic field at `P` due ot arc of circle

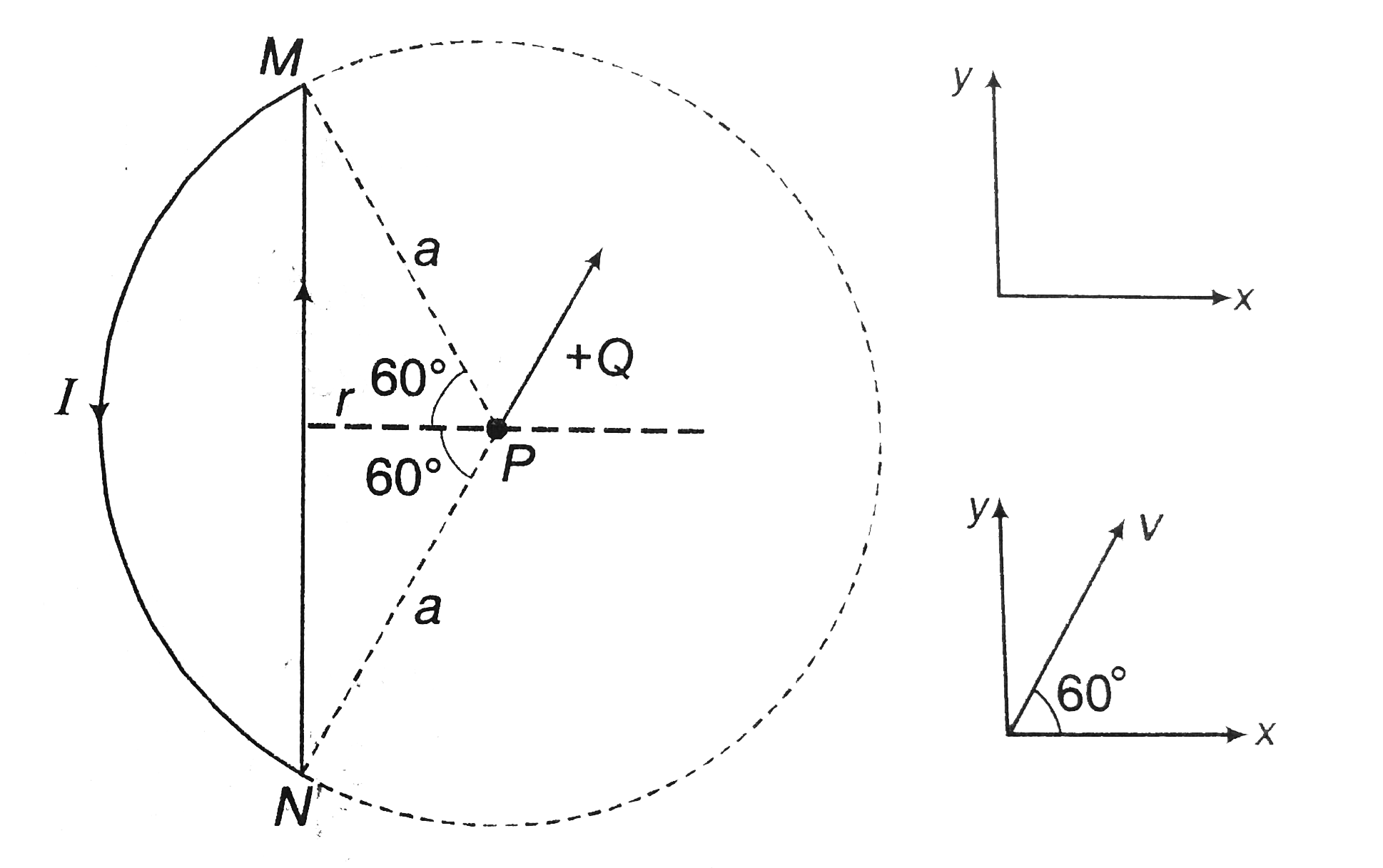
Subtending and angle of `120^@` at centre would be
`B_1=1/3("field due to circle")=1/3((mu_0I)/(2a))`
`=(mu_0I)/(6a)` [outwards]
`=(0.16mu_0I)/a` [outwards]
`B_1=(0.16mu_0I)/ahatk`
Magnetic field due to straight wire `NM` at P
`B_2=mu_0/(4pi) I/r(sin60^@+sin60^I@)`
here `racos60^@`
`:. B_2=mu_0/(4pi) I/(acos60^@)(2sin 60^@)`
or `B_2mu_0/(2pi) I/ tan 60^@`
`=(0.27mu_0I)/(a) ("inward")`
or`B_2=-(0.27mu_0I)/ahatk`
`:. B_(net)=B_1+B_2=-(0.11mu_0I)/ahatk`
Now, velocity of particle can be written as
`v=vcos60^@hati+vsin60^@hatj`
`=v/2hati+(sqrt3v)/2hatj`
magnetic force
`F_m=Q(vxxB)`
`=(0.11mu_0IQv)/(2a) hatj-(0.121sqrt3mu_IQv)/(2a) hati`
`:.` Instantaneous acceleration
`a=F_m/m=(0.11m_0IQv)/(2am)(hatj-sqrt3hati)`
b. In uniform magnetic field, force on a current loop is zero. further magnetic dipole moment of the loop will be
`M=(IA)hatk`
Here `A` is the area of the loop
`A=1/3(pia^2)-1/2[2xxasin60^@][acos60^@]`
`=pia^2/3-a^2/2sin120^I@`
`=0.61a^2`
`:. M=(0.61Ia^2)hatk`
Given, B`=`Bhati
`:. tau=MxxB=(0.61Ia^2B)hatj`
Promotional Banner

Topper's Solved these Questions

  • MAGNETICS

    DC PANDEY|Exercise Exercise|160 Videos

  • MAGNETICS

    DC PANDEY|Exercise INTRODUCTORY EXERCISE|1 Videos

  • MAGNETIC FIELD AND FORCES

    DC PANDEY|Exercise Medical entrance s gallery|59 Videos

  • MAGNETISM AND MATTER

    DC PANDEY|Exercise Medical gallery|1 Videos

Similar Questions

Explore conceptually related problems

A wire loop carrying I is placed in the x-y plane as shown in fig. (a) If a particle with charge +Q and mass m is placed at the centre P and given a velocity vec(v) along NP (see figure), find its instantaneous acceleration. ( b) If an external uniform magnetic induction field vec(B) = Bhat(i) is applied , find the force and the torque acting on the loop due to this field.

A wire loop carrying a current I is placed in the x-y plane. (a) If a particle with charge +Q and mass m is placed at the center P and given a velocity vec(v) along NP, find its acceleration. (b) if an external uniform magnetic induction vec(B) =B hat(i) is applied, find the force and the torque acting on the top due to this field.

A wire loop carrying current I is placed in the x-y plane as shown. Magnetic induction at P is

A circular loop carrying a current I is placed in the xy-plane as shown in figure. A uniform magnetic fied B is oriented along the positive z-axis. The loop tends to

A wire loop carrying current I is placed in the x-y plane as shown in the figure. If an external uniform magnetic field vec(B)=B hat(i) is switched on, then the torque acting on the loop is

A square loop of side l carries a current i. it is placed as shown in figure. Find the magnetic moment of the loop.

A circular loop of radius R is bent along a diameter and given a shape as shown in figure. One of 30, A the se micircles (KNM) lies in the xz-plane and the other one (KLM) in the yz-plane with their centres at origin. Current I is flowing through each of the semicircles as shown in figure. (a) A particle of charge q is released at the origin with a velocity v =- v_0hati . Find the instantaneous force F on the particle. Assume that space is gravity free. (b) If an external uniform magnetic field B_0hatj is applied, determine the force F_1 and F_2 on the semicircles KLM and KNM due to the field and the net force F on the loop.