Home
Class 12
PHYSICS
A flat dielectric disc of radius R carri...

A flat dielectric disc of radius `R` carries an exces charge on its surface. The surface charge density `sigma`. The disc rotastes about an axis perpendicular to its lane passing thrugh the centre with angulasr velocity `omega`. Find the toruque on the disc if it is placed in a uniform magnetic field `B` directed perpendicular to the rotation axis.

Text Solution

Verified by Experts

Consider an anular ring of radius `r` and of thickness dr on this disc. Charge within this ring,

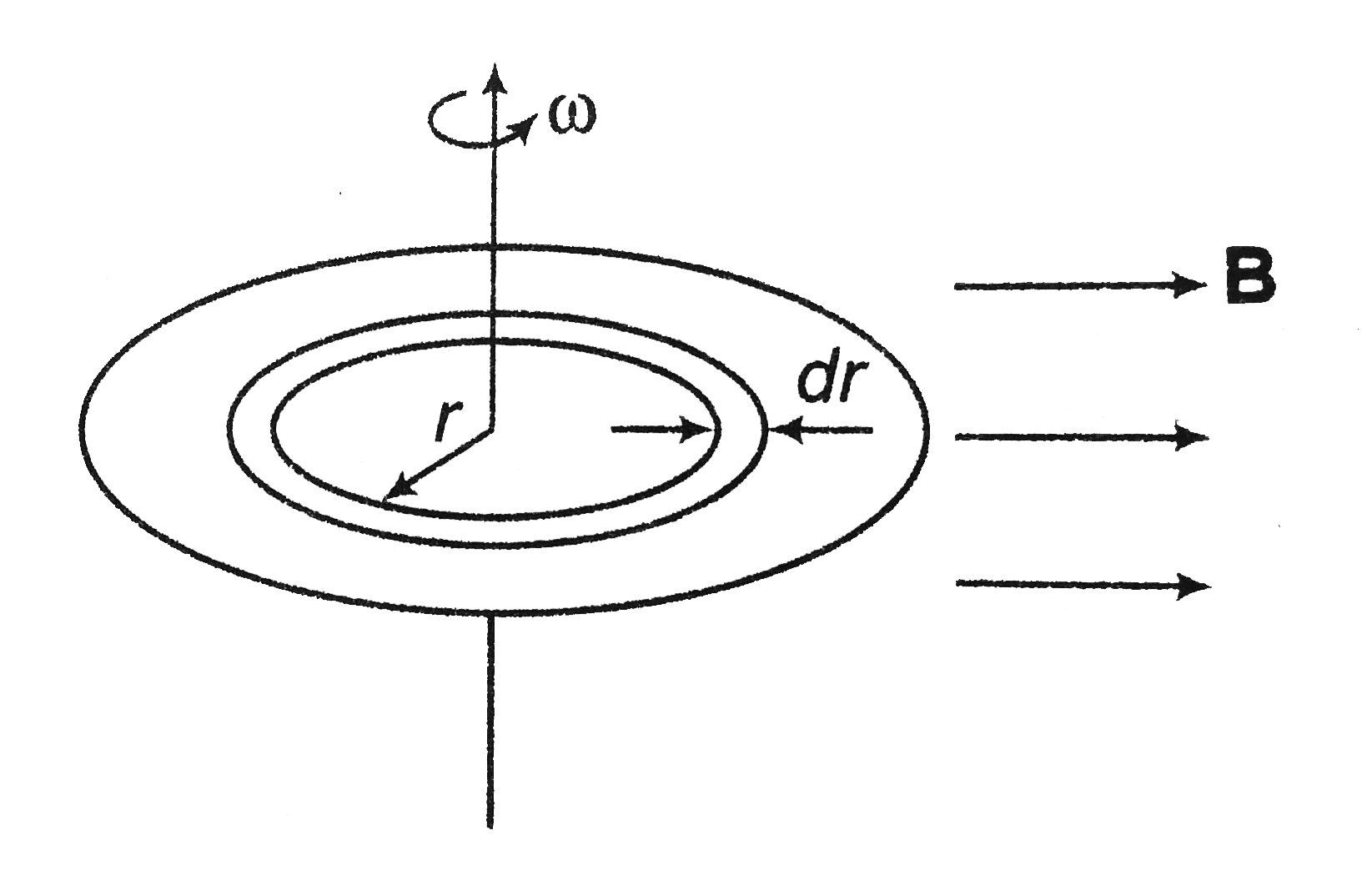
As ring rotates with angular velocity `omega`, the equivalent current is
`i=(dq)("frequency")`
`(sigma)(2pidr)(omega(2pi)) or i=sigmadrdr`
`=(sigma)(2pidr)(omega(2pi))or i=sigmardr`
Magnetic moment of this anulalr ring,
`M=iA=(sigmadr)(pir^2) ("along the axis of rotation")`
Torque on this ring
`dtau=MBsin90^@=(sigmapir^3B)dr`
`:.` Total torque on the disc is `tau=int_0^Rtau(sigmaomegapiB)int_0^Rr^3dr`
`=(sigmaomegaBR^4)/4`
Promotional Banner

Topper's Solved these Questions

  • MAGNETICS

    DC PANDEY|Exercise Exercise|160 Videos

  • MAGNETICS

    DC PANDEY|Exercise INTRODUCTORY EXERCISE|1 Videos

  • MAGNETIC FIELD AND FORCES

    DC PANDEY|Exercise Medical entrance s gallery|59 Videos

  • MAGNETISM AND MATTER

    DC PANDEY|Exercise Medical gallery|1 Videos

Similar Questions

Explore conceptually related problems

Radius of gyration of disc rotating about an axis perpendicular to its plane passing through through its centre is (If R is the radius of disc)

A flat insulating disc of radius 'a' carries an excess charge on its surface is of surface charge density sigma C//m^(2) . Consider disc to rotate around the perpendicular to its plane with angular speed omega rad//s / If magnetic field vec(B) is directed perpendicular to the roation axis, then find the torque acting on the disc.

A disc of mass m has a charge Q distributed on its surface. It is rotating about an XX' with a angular velocity omega . The force acting on the disc is

A sphere of radius R, uniformly charged with the surface charge density sigma rotates around the axis passing through its centre at an angular velocity. (a) Find the magnetic induction at the centre of the rotating sphere. (b) Also, find its magnetic moment.

Find the moment of inertia of a uniform half-disc about an axis perpendicular to the plane and passing through its centre of mass. Mass of this disc is M and radius is R.

A flat disc of radius R charged uniformly on its surface at a surface charge density sigma . About its central axis of rotation it rotates at an angular speed omega . Find the magnetic moment of disc due to rotation of charges.

A charge Q is uniformly distributed over the surface of non - conducting disc of radius R . The disc rotates about an axis perpendicular to its plane and passing through its centre with an angular to its plane and passing through its centre of the disc. If we keep both the amount of charge placed on the disc and its angular velocity to be constant and vary the radius of the disc then the variation of the magnetic induction at the centre of the disc will br represented by the figure:

A nonconducing disc of radius R is rotaing about axis passing through its cente and perpendicual its plance with an agular velocity omega . The magnt moment of this disc is .

Two thin discs each of mass M and radius r are attached as shown in figure, to from a rigid body. The rotational inertia of this body about an axis perpendicular to the plane of disc B and passing through its centre is : .