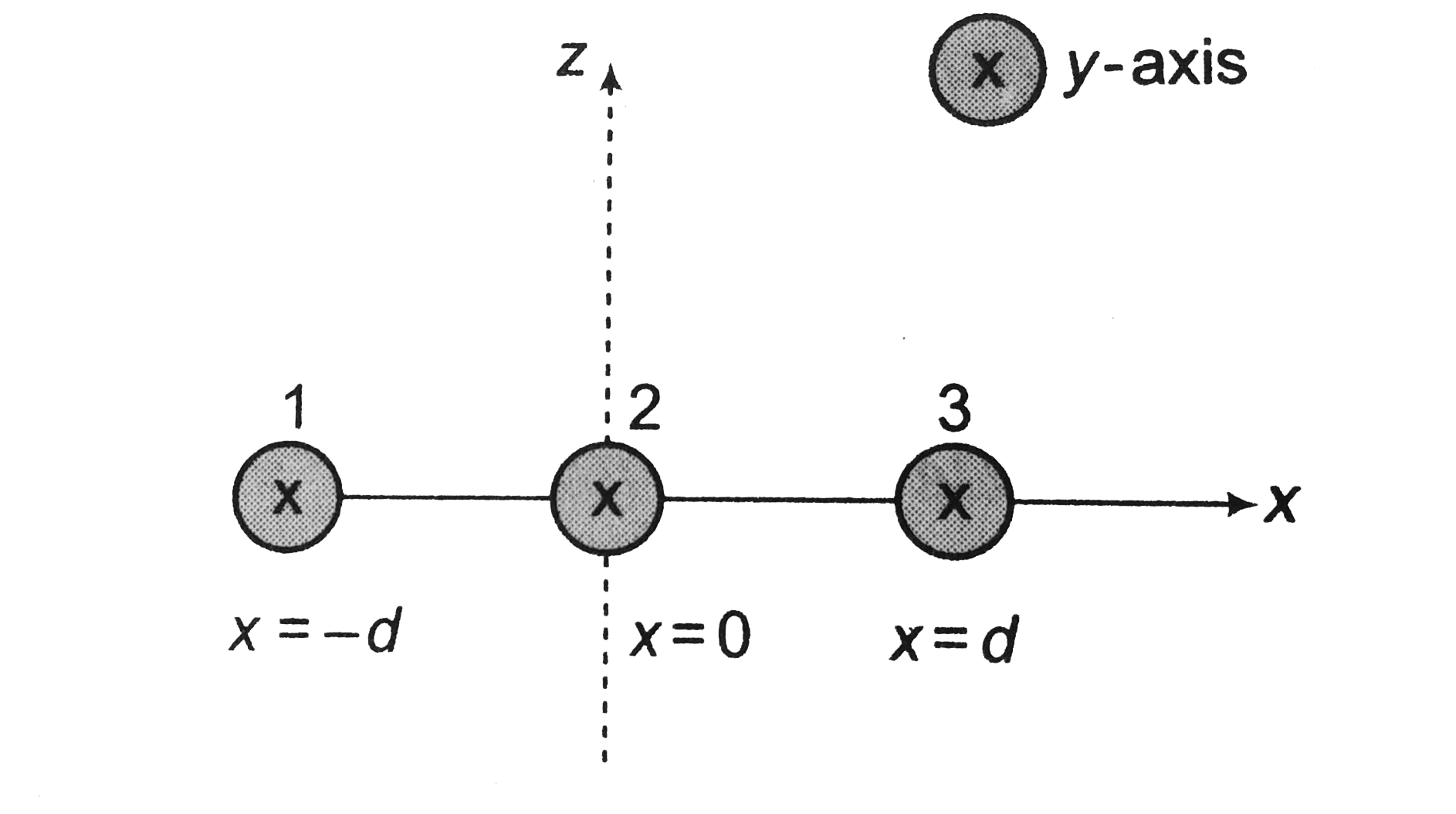
Three infinitely long thein wires, each carrying curren i int eh same diecrtion, are the dxy plane of a gravilty free space. The central wire is along the y-axis while the other two are along `x=+-d`
i find the locus of the points for which the magnetic field `B` is zero.
ii If the central wire is displaced along the `z`-direction by a smal amount and released, show that it will execute simple harmonic motion. If the linear mass density of the wires is `lamda`, find the frequency of oscillation.
Three infinitely long thein wires, each carrying curren i int eh same diecrtion, are the dxy plane of a gravilty free space. The central wire is along the y-axis while the other two are along `x=+-d`
i find the locus of the points for which the magnetic field `B` is zero.
ii If the central wire is displaced along the `z`-direction by a smal amount and released, show that it will execute simple harmonic motion. If the linear mass density of the wires is `lamda`, find the frequency of oscillation.
i find the locus of the points for which the magnetic field `B` is zero.
ii If the central wire is displaced along the `z`-direction by a smal amount and released, show that it will execute simple harmonic motion. If the linear mass density of the wires is `lamda`, find the frequency of oscillation.
Text Solution
Verified by Experts
i. Magnetic field will be zero on the `y`-axis i.e.` x=0=z`

Magnetic field cannot be zero in region I and egion IV because in reion I magnetic field will be along positive z-direction due to all the three wires, while in region IV magnetic field will be along negative z-axis due to all the three wires. It can be zero only i reginn II and III.
Let magnetic field is zero on line `z=0` and `x=x` (shown as dotted). The magnetic field on the line due to wire 1 and 2 will be along negative z-axis and due to wire 3 along positive z-axis. Thus,

`B_1+B_2=B_3`
or `mu_0/(2pi) i/((d+x))+(mu_0i)/(2pix)=mu_0/(2pi) i/((d-x))`
`or 1/(d+x)+1/x=1/(d-x)`
this equation gives `x=+-d/sqrt3`
Hence there will be two lilnes `x=d/sqrt3`
and `x=-d/sqrt3 (z=0)`
where magnetic field is zero.
ii. In this part we chasnge our coordinate axes sytem, just for better understanding.
There are three wires 1,2, and 3 as shown in figure. Ilf we displace the wire 2 towards the z-axis, then force of attraction per unit length between wire (1 and 2) and (2 and 3) will be given by
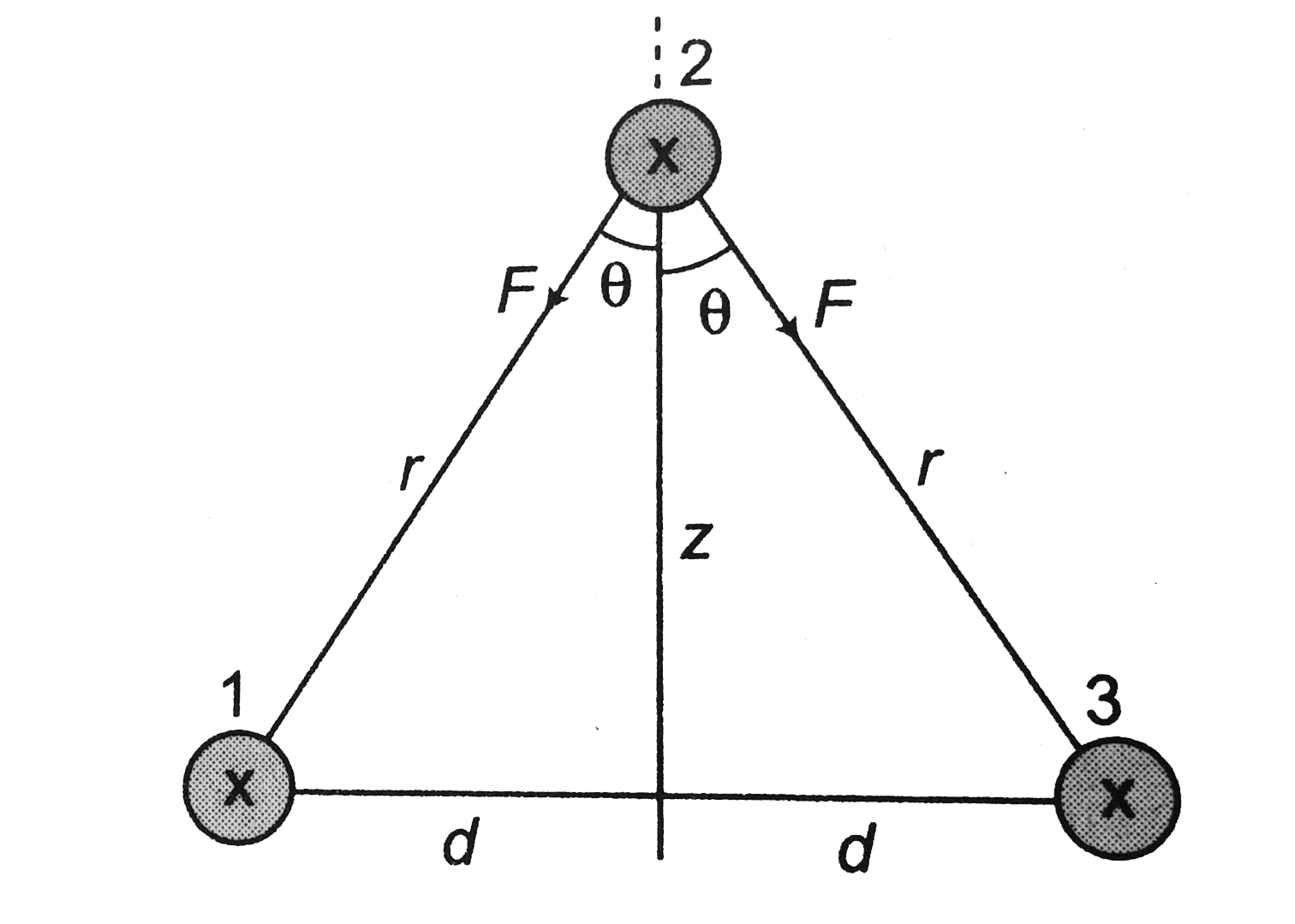
`f=mu_0/(2pi) i^2/r`
The componetns of `F` along x-axis will be canceled out. Net resultant force will be towards negative z-axis (or mean position) and will be given by
`F_("net")=2Fcostheta=2{mu_0/(2pi)i^2/r}z/r`
`F_("net")=mu_0/pi i^2(z^2+d^2).z(r^2=z^2+d^2)`
If `zltltd` then
`z^2d^2=d^2`
and `F_("net")=(mu_0/pi i^2/d^2).z`
Negative sign implies that `F_("net")` is restoring in nature.
`therefore, F_("net") prop-z`
i.e. the wire will oscillate simple harmonically,
let a be the acceleration of wire in this position and `lamda` the mass per unit length of wire, then
`F_("net") =lamda a-(mu_0/pii^2/d^2)z`
`or ap=((m_0i^2)/(pilamdad^2))z`
`:. `Frequency of oscillation
`f=1/(2pi) sqrt(|"acceleration")/("displacement"|)`
`1/(2pi) sqrt(|a/z|=1/(2pi) i/d sqrt(m_0/(pilamda))`
or `f=1/(2pid) sqrt(mu_0)/(pilamda))`

Magnetic field cannot be zero in region I and egion IV because in reion I magnetic field will be along positive z-direction due to all the three wires, while in region IV magnetic field will be along negative z-axis due to all the three wires. It can be zero only i reginn II and III.
Let magnetic field is zero on line `z=0` and `x=x` (shown as dotted). The magnetic field on the line due to wire 1 and 2 will be along negative z-axis and due to wire 3 along positive z-axis. Thus,

`B_1+B_2=B_3`
or `mu_0/(2pi) i/((d+x))+(mu_0i)/(2pix)=mu_0/(2pi) i/((d-x))`
`or 1/(d+x)+1/x=1/(d-x)`
this equation gives `x=+-d/sqrt3`
Hence there will be two lilnes `x=d/sqrt3`
and `x=-d/sqrt3 (z=0)`
where magnetic field is zero.
ii. In this part we chasnge our coordinate axes sytem, just for better understanding.

There are three wires 1,2, and 3 as shown in figure. Ilf we displace the wire 2 towards the z-axis, then force of attraction per unit length between wire (1 and 2) and (2 and 3) will be given by

`f=mu_0/(2pi) i^2/r`
The componetns of `F` along x-axis will be canceled out. Net resultant force will be towards negative z-axis (or mean position) and will be given by
`F_("net")=2Fcostheta=2{mu_0/(2pi)i^2/r}z/r`
`F_("net")=mu_0/pi i^2(z^2+d^2).z(r^2=z^2+d^2)`
If `zltltd` then
`z^2d^2=d^2`
and `F_("net")=(mu_0/pi i^2/d^2).z`
Negative sign implies that `F_("net")` is restoring in nature.
`therefore, F_("net") prop-z`
i.e. the wire will oscillate simple harmonically,
let a be the acceleration of wire in this position and `lamda` the mass per unit length of wire, then
`F_("net") =lamda a-(mu_0/pii^2/d^2)z`
`or ap=((m_0i^2)/(pilamdad^2))z`
`:. `Frequency of oscillation
`f=1/(2pi) sqrt(|"acceleration")/("displacement"|)`
`1/(2pi) sqrt(|a/z|=1/(2pi) i/d sqrt(m_0/(pilamda))`
or `f=1/(2pid) sqrt(mu_0)/(pilamda))`
Topper's Solved these Questions
Similar Questions
Explore conceptually related problems
Three infinitely long thin wires, each carrying current i in the same direction, are in the x-y plane of a gravity free space . The central wire is along the y - axis while the other two are along x = +-d . (i) Find the locus of the points for which the magnetic field B is zero. (ii) If the central wire is displaced along the Z- direction by a small amount and released, show that it will excecute simple harmonic motion . If the linear density of the wires is lambda , find the frequency of oscillation.
Three infinitely long thin wires each carrying current I in the same direction are in x-y plane of a gravity free space. The central wire is along the y -axis while the other two are along x=+-d . If the central wire is slightly displaced along z -axis and released, show that it will execute S.H.M . The linear mass density of the wire is lambda . If the time period of this small oscillation is (kpid)/(I)sqrt((pilambda)/(mu_(0))) , then find the value of k .
Two infinitely long wires each carrying current I along the same direction are made into the geometry as shown in the figure. The magnetic field at the point P is
Three infinitely long wires,each carrying equal current are placed in the xy -plane along x= 0,+d and -d .On the xy -plane,the magnetic field vanishes at
Two infinitely long parallel wires carry equal current in same direction. The magnetic field at a mid point in between the two wires is
Three long wires, each carrying current i are placed as shown. The middle wire is along Y -axis. The locus of point on the X -axis where magnetic field is zero is
Two long wire carrying current 2i and i are placed along co-ordinate axes x and y respectively. The locus of point where magnetic field is zero is
Three infinitely long wires, each carrying a current 1A, are placed such that one end of each wire is at the origin, and, one of these wires is along x-axis, the other along y-axis and the third along z-axis. Magnetic induction at point (-2 m, 0, 0) due to the system of these wires can be expressed as
two infinite wires, carrying currents i_1 and i_2 ., are lying along x-and y-axes, as shown in the x-y plane. Then,