Home
Class 12
PHYSICS
Uniform electrilcf and magnetic fields w...

Uniform electrilcf and magnetic fields with strength E and B are directed along of x-axis. A particle with specific charge `q/m` leves the origin in the direction of x-axis with an initial velocity `v_0`. Find
a. the y-coordinate of the particle when it crosses the y-xis for nth time.
b. the angle `alpha` between the particle's velocity vector adn the y-axis for nth time

Text Solution

Verified by Experts

a. As discussed in type 9 path of the particle is a helix of incresing pitch. The axis of the helix is parallel to y-axis (parrallell to `E`) nd plane of circle of the helix is `xz` (perendicular to `B`). The particle will cross the y-axis after time.
`t=hT-n((2pim)/(Bq))=(2pimn)/(Bq)`
The y-coordinate of particle at this instant is
`y=1/2a_yt^2`
`a_y=F_y/m=(qE)/m`
`:. y=1/2((qE)/m)((2pimn)/(Bq))^2`
`=(2n^2mEpi^2)/(qB^2)`
At this moment y-component of its velocity is
`v_y=a_yt=((qE)/(m))((2pimn)/(Bq))=2pin(E/B)`

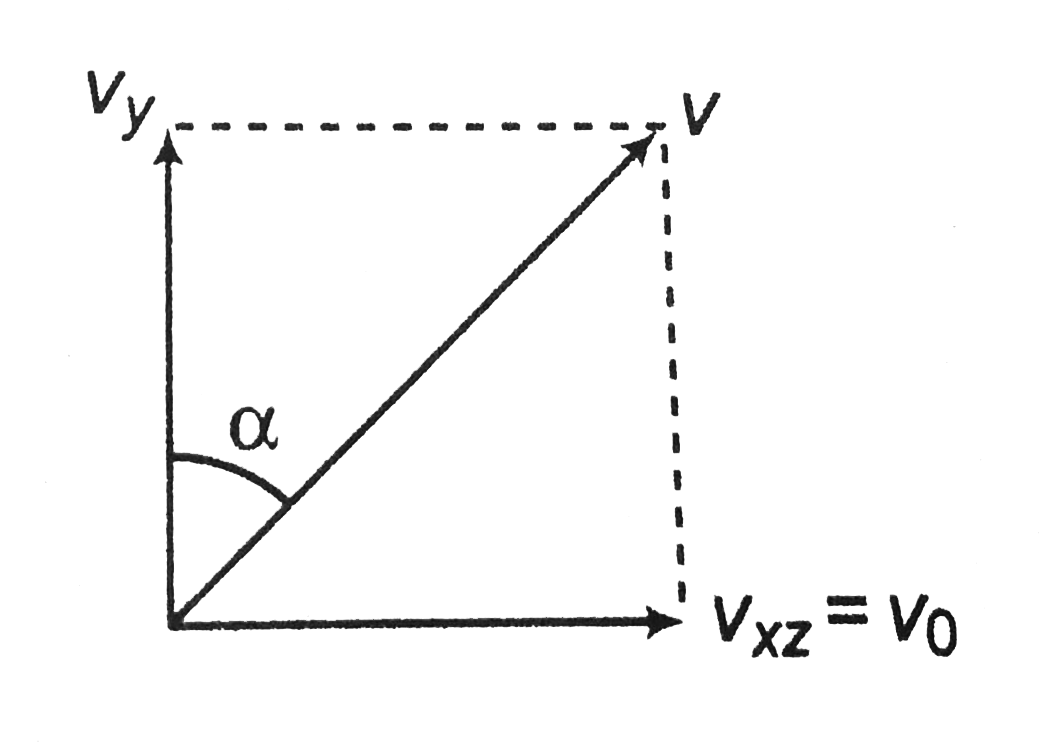
`alpha=tan^-1(v_(xz)/v^-y)`
`Here, v_(xz)=sqrt(v_x^2+v_2^2)=v_0`
`or alpha=tan^-1((Bv_0)/(2pinE))`
Promotional Banner

Topper's Solved these Questions

  • MAGNETICS

    DC PANDEY|Exercise Exercise|160 Videos

  • MAGNETICS

    DC PANDEY|Exercise INTRODUCTORY EXERCISE|1 Videos

  • MAGNETIC FIELD AND FORCES

    DC PANDEY|Exercise Medical entrance s gallery|59 Videos

  • MAGNETISM AND MATTER

    DC PANDEY|Exercise Medical gallery|1 Videos

Similar Questions

Explore conceptually related problems

Uniform electric and magnetic fields with strength E and induction B, respectively, are along y-axis as shown in Fig. A particle with specific charge q//m leaves the origin O in the direcction of x-axis with an initial non-relativistic velocity v_0 The coordinate y_n of the particle when it crosses the y-axis for the n^(th) time is

Uniform electric and magnetic fields with strength E and induction B, respectively, are along y-axis as shown in Fig. A particle with specific charge q//m leaves the origin O in the direcction of x-axis with an initial non-relativistic velocity v_0 The angle alpha between the particle's velocity vector and y-axis at and moment is

Uniform electric field E and magnetic field B, respectively, are along y-axis as shown in the figure. A particle with specific charge q/m leaves the origin O in the direction of x-axis with an initial non-relativistic speed v_(0) . The angle alpha between the particle’s velocity vector and y-axis at that moment is:

A charged particle (charge q, mass m) has velocity v_(0) at origin in +x direction. In space there is a uniform magnetic field B in -z direction. Find the y coordinate of particle when is crosses y axis.

There exist uniform magnetic and electric fields of manitudes 1T and 1Vm^-1 respectively, along positive y-axis. A charged particle of mass 1kg and charge 1C is having velocity 1ms^-1 along x-axis and is at origin at t=0. Then, the coordinates of the particle at time pis will be

A particle of mass m and charge q is lying at the origin in a uniform magnetic field B directed along x-axis. At time t = 0, it is given a velocity v_0 , at an angle theta with the y-axis in the xy-plane. Find the coordinates of the particle after one revolution.

A positively charged particle with specific charge sigma leaves the origin with a velocity u directed along positive x direction. The entire space has a uniform electric field (E) and magnetic field (B) directed along the positive y direction. Find the angle that the velocity of the particle makes with y direction at the instant it crosses the y axis for n^(th) time.

A charge particle of mass m and charge q is projected with velocity v along y-axis at t=0. Find the velocity vector and position vector of the particle vec v (t) and vec r (t) in relation with time.

A particle of mass m, carrying a charge q, is lying at the origin in a uniform magentic field directed along X axis. At the instant t = 0 it is given a velocity v_(a) at an angle theta with the y-axis, in the XY plane. The coordinates of the particle after two revolution will be