A particle of charge `q` and mass `m` is projected from the origin with velocity `v=v_0 hati` in a non uniformj magnetic fiedl `B=-B_0xhatk`. Here `v_0` and `B_0` are positive constants of proper dimensions. Find the maximum positive x coordinate of the particle during its motion.

Explanation

Magnetic field is along negative z-direction. So in the coordinate axes sonw in figure, it is perpendicular to paper inwards. Mgnetic force on the particle at origin is along positive y-directio. So, it will rotat in xy-plane as shown. The path is not a perfect circle as the magnetic field is non uniform. Speed of the particle in magnetic field remains constant. Magnetic force is always perpendiculr to velocity. Let at point P(x,y) its velocity vector makes an angle theta with positive x-axis. The magnetic force `F_m` will be angle `theta` with positive y-direction.So,

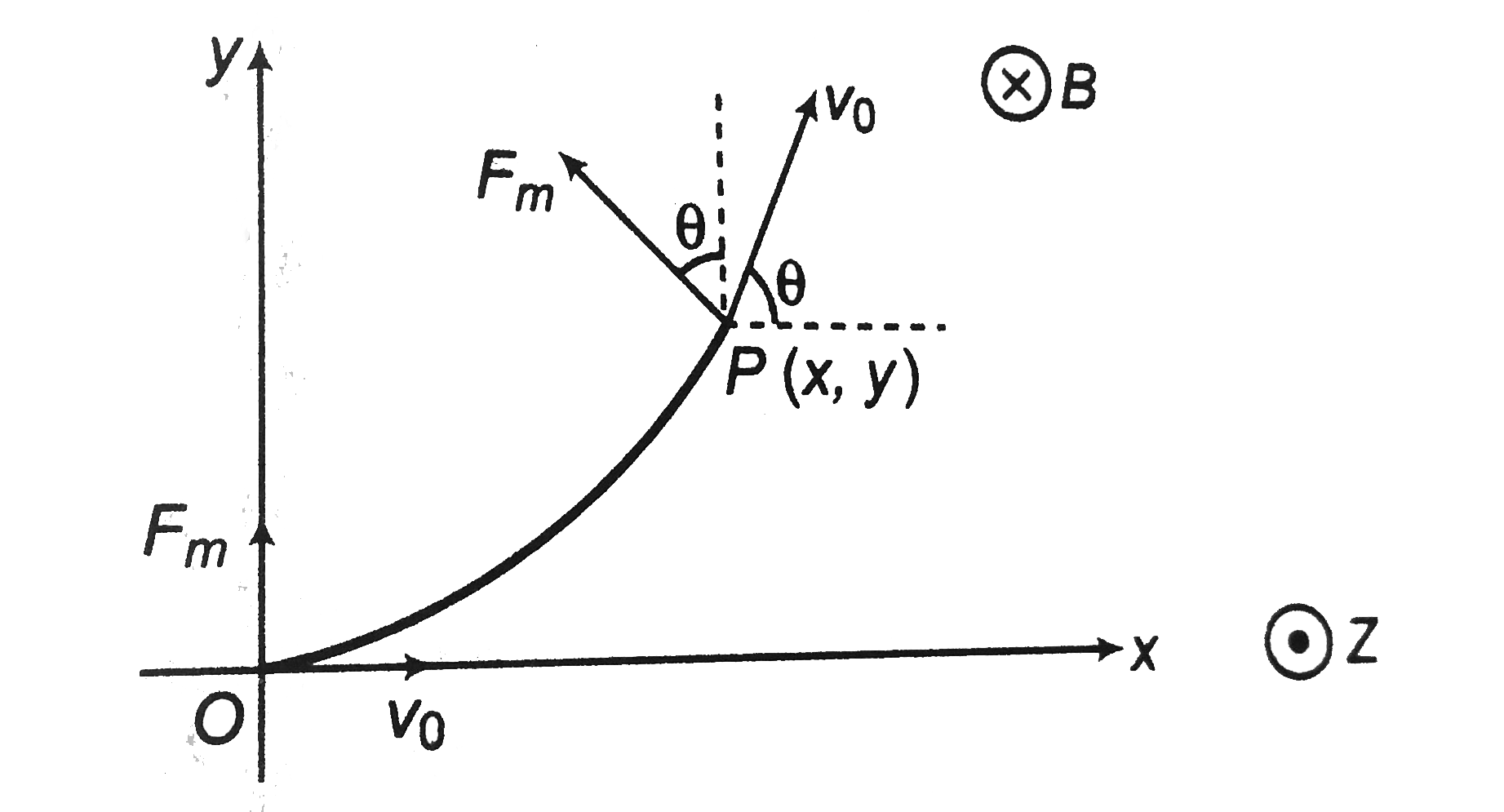
`a_y=(F_m/m)costheta`
`:. (dv_y)/(dt)=((B_0x)(qv_)costheta)0/m [F_m=Bqv_0sin90^@]`
`:. ((dv_(y))/(dx)).((dx)/(dt))=(B_0qx)/m(v_0costheta)`
`Here, (dx)/(dt)=v_x=v_0costheta`
`:. (dv_y)/(dx)=((B_0q)/(m))x`
`:. int_0^(v_0) dv_y=((B_0q)/m)int_0^(x_max) xdx`
`:. v_0=((B_0q)/m)(x_(max)^2)/(2)`
`:. x_(max)=sqrt((mv_02)/(B_0q))`