लिखित उत्तर
Verified by Experts
टॉपर्स ने हल किए ये सवाल
त्रिभुजों की सर्वांगसमता
KC SINHA|Exercise अभ्यास 9.1 (अतिलघु उत्तरीय प्रश्न )|36 Videosत्रिभुजों की सर्वांगसमता
KC SINHA|Exercise अभ्यास 9.1 लघु उत्तरीय प्रश्न|11 Videosज्यामितीय बनावट ( रचनाएँ )
KC SINHA|Exercise उदाहरण|11 Videosदो चरों वाले रैखिक समीकरण
KC SINHA|Exercise वस्तुनिष्ट प्रश्न|15 Videos
KC SINHA-त्रिभुजों की सर्वांगसमता -वस्तुनिष्ठ प्रश्न
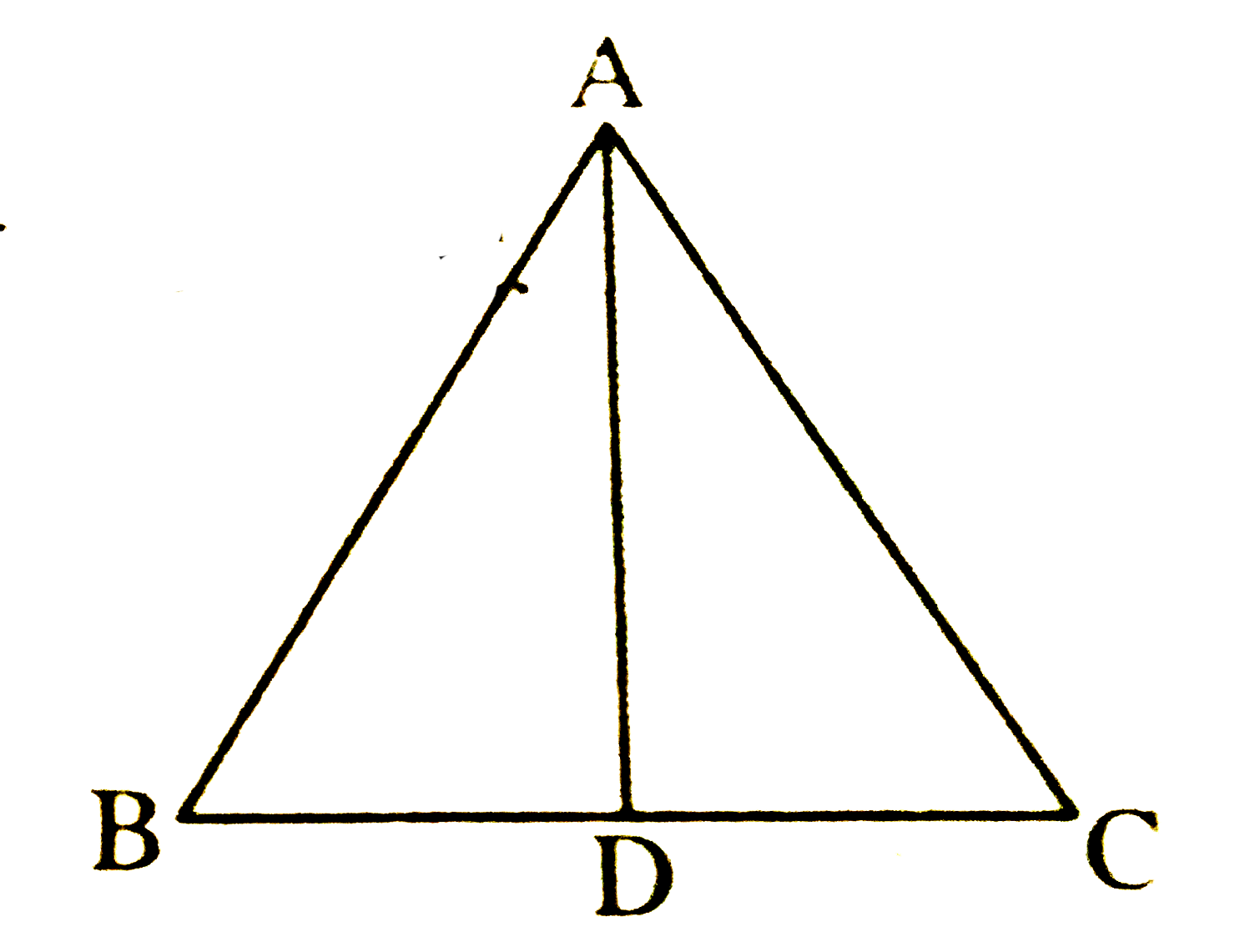
- AD एक समद्विबाहु त्रिभुज ABC का एक शीर्षलम्ब है, जिसमें AB = AC है | द...
Text Solution
|
- निम्न चित्र में x का मान है:
Text Solution
|
- बगल के चित्र में AB || CD तो y का मान है
Text Solution
|
- बगल के चित्र में x का मान है
Text Solution
|
- बगल के चित्र में angleBEC बराबर है
Text Solution
|
- बगल के चित्र में angleBAC बराबर है
Text Solution
|
- बगल के चित्र में angleQPR बराबर है
Text Solution
|
- बगल के चित्र में x बराबर है
Text Solution
|
- बगल के चित्र में AB||CD, angleQPR बराबर है
Text Solution
|