लिखित उत्तर
Verified by Experts
टॉपर्स ने हल किए ये सवाल
समांतर चतुर्भुज
KC SINHA|Exercise अतिलघु उत्तरीय प्रश्न (समांतर चमुर्भुज, आयत, वर्ग तथा समचतुर्भुज से संबंधित परिभाषाओं, प्रमेयों तथा उपप्रमेयों के सीधे प्रयोग पर आधारित प्रश्नः)|16 Videosसमांतर चतुर्भुज
KC SINHA|Exercise लघु उत्तरीय प्रश्न|4 Videosवृत्त
KC SINHA|Exercise वस्तुनिष्ठ प्रश्न|17 Videosसमांतर चतुर्भुजों और त्रिभुजों के क्षेत्रफल
KC SINHA|Exercise वस्तुनिष्ट प्रश्न|7 Videos
KC SINHA-समांतर चतुर्भुज-वस्तुनिष्ठ प्रश्न
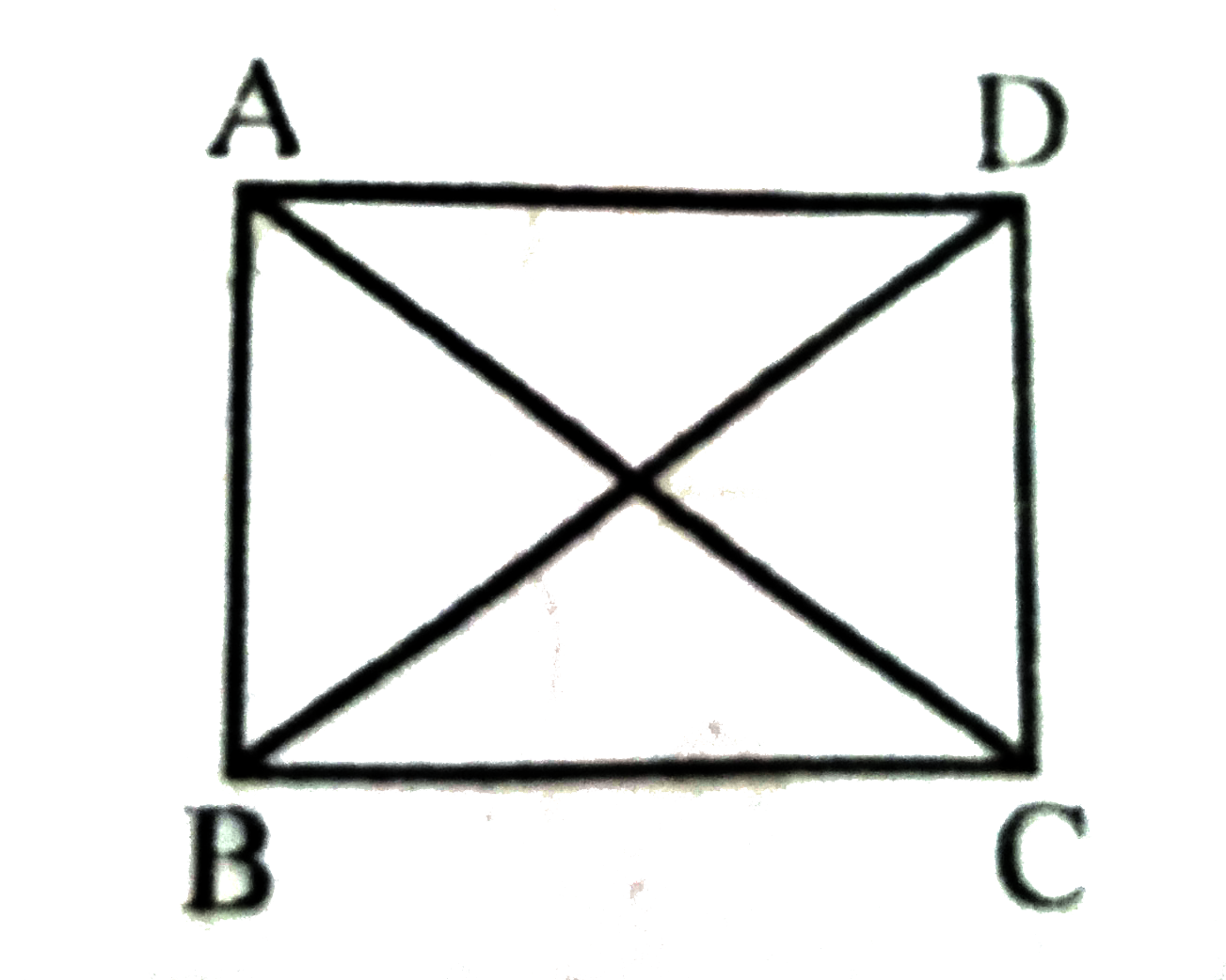
- यदि एक समांतर चतुर्भुज के विकर्ण बराबर हों, तो दर्शाइए कि वह एक आयत है...
Text Solution
|
- चतुर्भुज के चारों कोणों का योग कितना समकोण होता है?
Text Solution
|
- समांतर चतुर्भुज के सम्मुख कोण होते हैं
Text Solution
|
- समांतर चतुर्भुज के विकर्ण
Text Solution
|
- निम्नलिखित में कौन सत्य है?
Text Solution
|
- निम्नलिखित में कौन असत्य है?
Text Solution
|
- निम्नलिखित में कौन सत्य है?
Text Solution
|
- बगल के चित्र में ABCD एक समांतर चतुर्भुज है तो /BAC बराबर है
Text Solution
|
- बगल के चित्र में ABCD समचतुर्भुज है इसके विकर्ण O पर मिलते हैं तथा /OA...
Text Solution
|
- बगल के चित्र में AL और CM समांतर चतुर्भुज ABCD के विकर्ण BD पर लंब हैं...
Text Solution
|