लिखित उत्तर
Verified by Experts
टॉपर्स ने हल किए ये सवाल
लम्ब वृत्तीय शंकु
KC SINHA|Exercise EXERCISE-17|46 Videosलम्ब वृत्तीय शंकु
KC SINHA|Exercise वस्तुनिष्ठ प्रश्न|7 Videosलम्ब वृतीय बेलन
KC SINHA|Exercise वस्तुनिष्ट प्रश्न|10 Videosवास्तविक संख्याएं
KC SINHA|Exercise उत्तरोत्तर आवर्धन द्वारा संख्या रेखा पर परिमेय संख्या का निरूपण देखने पर आधारित प्रश्नः|3 Videos
KC SINHA-लम्ब वृत्तीय शंकु -वस्तुनिष्ठ प्रश्न
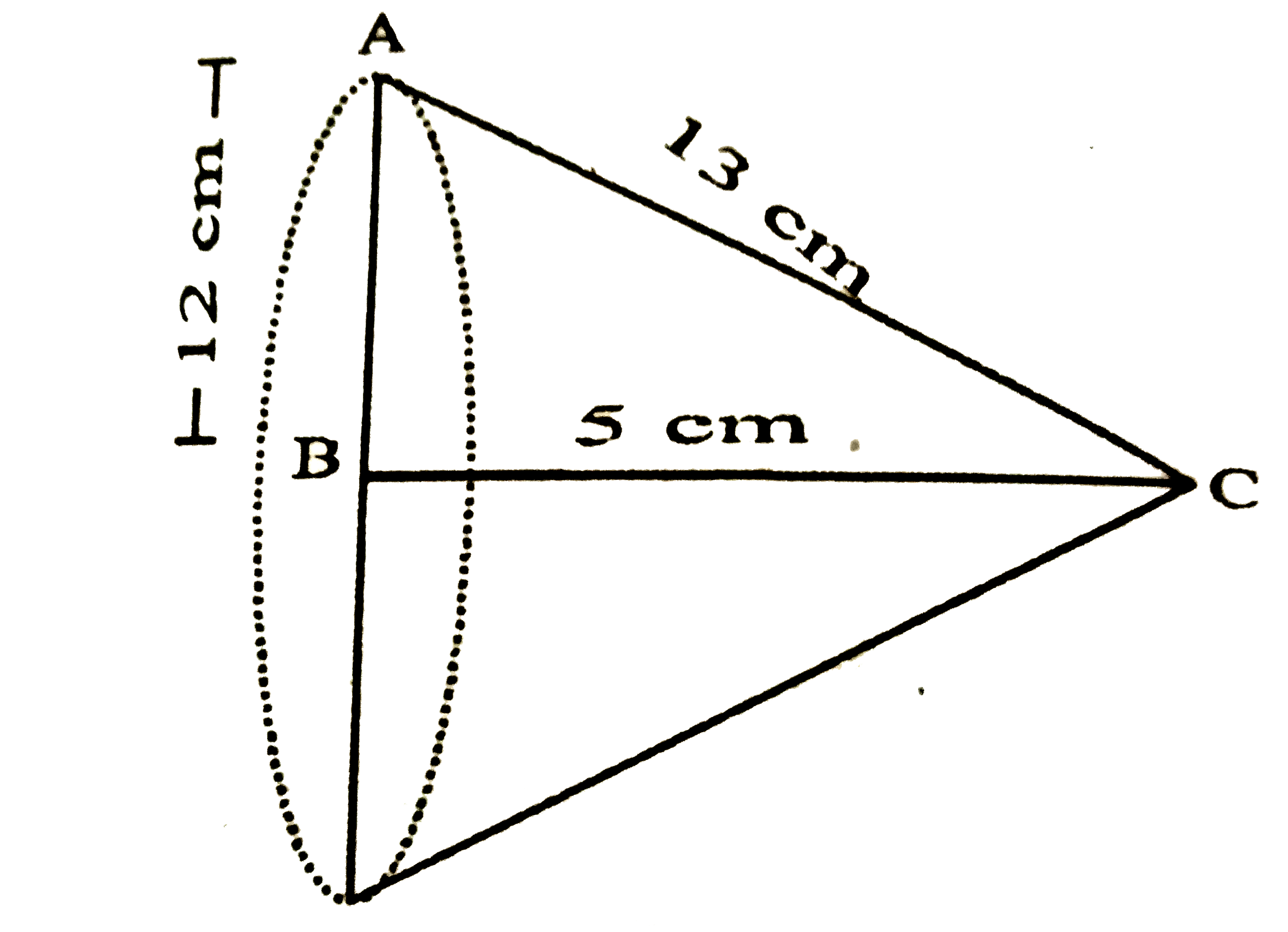
- भुजाओं 5 cm , 12 cm और 13 cm वाले एक समकोण त्रिभुज ABC को यदि 5 cm भ...
Text Solution
|
- 24 मीटर ऊँचे शंकुकार तम्बू के आधार की परिधि 44 मीटर है। इस तम्बू को ब...
Text Solution
|
- एक लंबवृत्तीय शंकु के आधार की त्रिज्या 7 सेमी और ऊँचाई 24 सेमी है। कुल...
Text Solution
|
- किसी शंकु की ऊँचाई और आधार की त्रिज्या दोनों को 100 % बढ़ा दिया जाए तो...
Text Solution
|
- 25 सेमी तिर्यक ऊँचाई वाले शंकु के वक्रपृष्ठ का क्षेत्रफल 550 "सेमी"^(...
Text Solution
|
- एक लंबवृतीय शंकु की ऊँचाई 4 मी है और इसके आधार की त्रिज्या 3 मी है। इस...
Text Solution
|
- दो शंकुओं की ऊँचाइयों का अनुपात 1 : 2 है एवं आधार-त्रिज्याओं का अनु...
Text Solution
|
- दो शंकु है जिनमें एक का वक्रपृष्ठ क्षेत्रफल दूसरे का दुगुना है , दूसर...
Text Solution
|