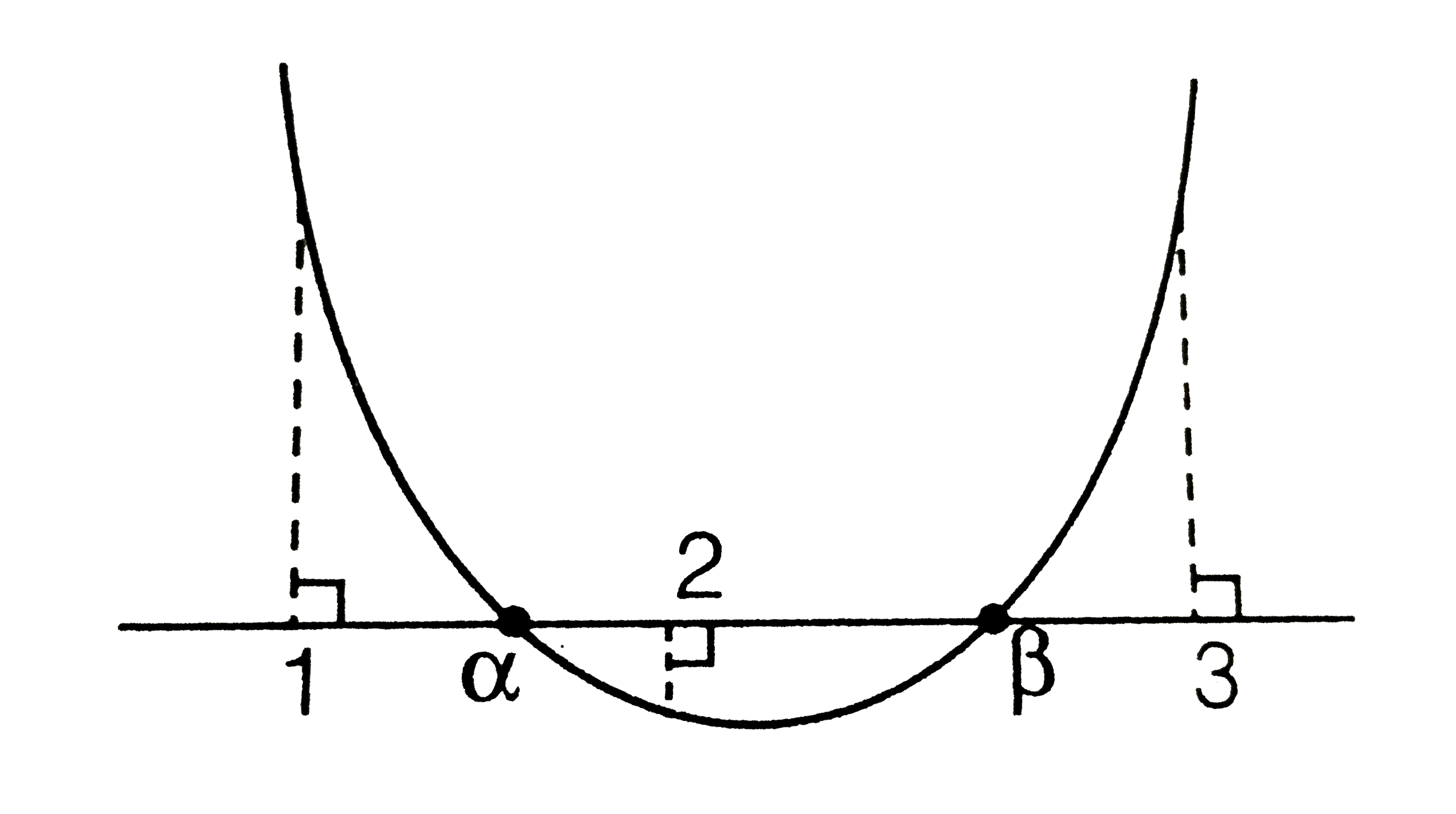
Text Solution
Verified by Experts
The correct Answer is:
Topper's Solved these Questions
THEORY OF EQUATIONS
ARIHANT MATHS|Exercise Exercise (Matching Type Questions)|2 VideosTHEORY OF EQUATIONS
ARIHANT MATHS|Exercise MATCH TYPE|2 VideosTHEORY OF EQUATIONS
ARIHANT MATHS|Exercise Exercise (Passage Based Questions)|21 VideosTHE STRAIGHT LINES
ARIHANT MATHS|Exercise Exercise (Questions Asked In Previous 13 Years Exam)|18 VideosTHREE DIMENSIONAL COORDINATE SYSTEM
ARIHANT MATHS|Exercise Exercise (Questions Asked In Previous 13 Years Exam)|44 Videos
Similar Questions
Explore conceptually related problems
ARIHANT MATHS-THEORY OF EQUATIONS-Exercise (Single Integer Answer Type Questions)
- The sum of all the real roots of the equation |x-2|^2+|x-2|-2=0 is
Text Solution
|
- The harmonic mean of the roots of the equation (5+sqrt(2))x^2-(4+sqrt(...
Text Solution
|
- If product of the real roots of the equation, x^(2)-ax+30=2sqrt((x^(2)...
Text Solution
|
- The minimum value of ((x+1/x)^6-(x^6+1/(x^6))- 2)/((x+1/x)^3+x^3+1/x^...
Text Solution
|
- Let a,b,c,d be distinct real numbers and a and b are the roots of the ...
Text Solution
|
- If the maximum and minimum values of y=(x^2-3x+c)/(x^2+3x+c) are 7 and...
Text Solution
|
- The number of solutions of the equation sqrt(x^(2))-sqrt((x-1)^(2))+...
Text Solution
|
- If alpha and beta are the complex roots of the equation (1+i)x^(2)+(1-...
Text Solution
|
- If alpha, beta be the roots of 4x^(8) - 16x + c = 0, c in R such that ...
Text Solution
|
- Let r,s and t be the roots of the equation 8x^(3)+1001x+2008=0 and if ...
Text Solution
|