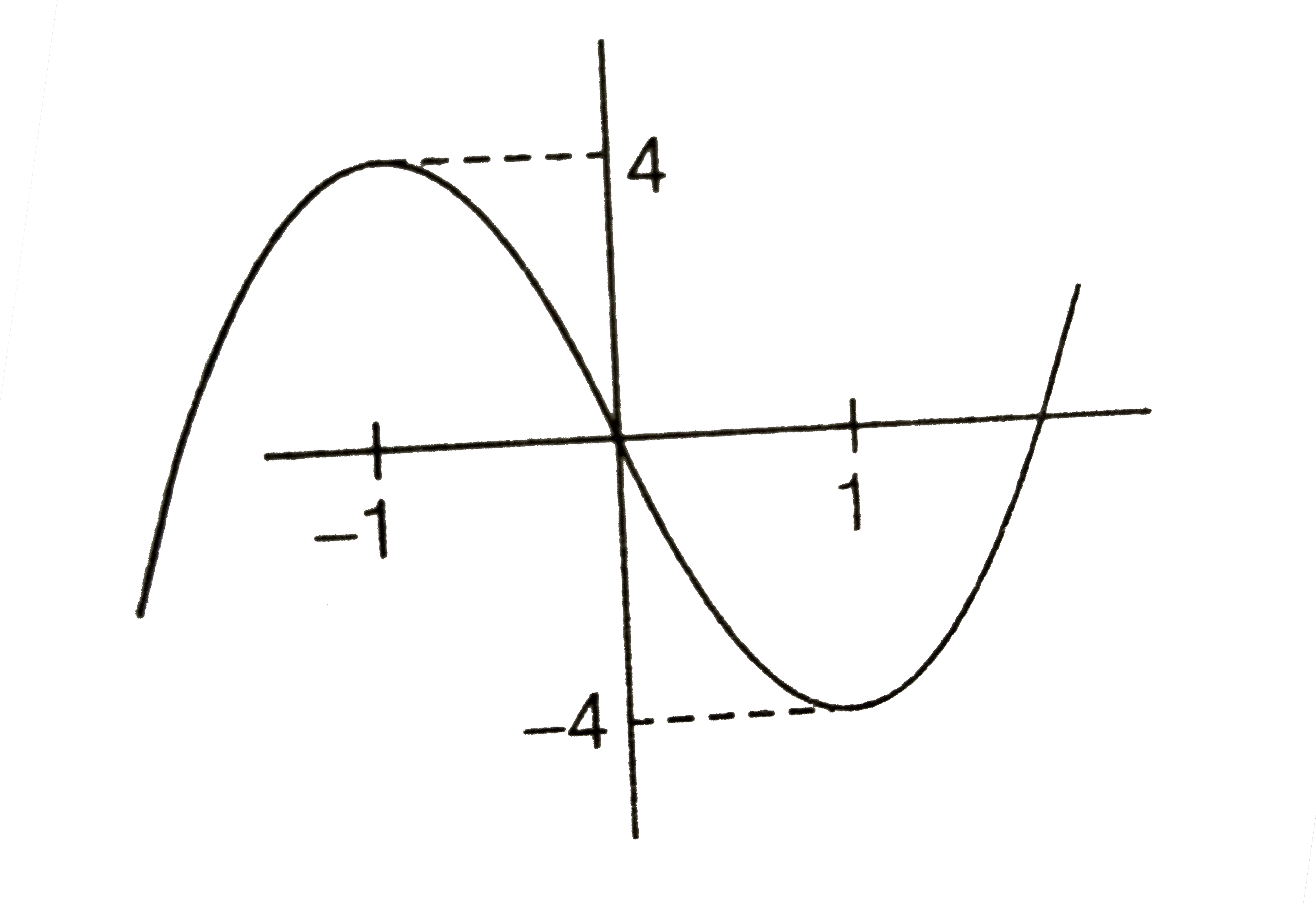
A
B
C
D
Text Solution
Verified by Experts
The correct Answer is:
Topper's Solved these Questions
THEORY OF EQUATIONS
ARIHANT MATHS|Exercise Exercise (Subjective Type Questions)|24 VideosTHE STRAIGHT LINES
ARIHANT MATHS|Exercise Exercise (Questions Asked In Previous 13 Years Exam)|18 VideosTHREE DIMENSIONAL COORDINATE SYSTEM
ARIHANT MATHS|Exercise Exercise (Questions Asked In Previous 13 Years Exam)|44 Videos
Similar Questions
Explore conceptually related problems
ARIHANT MATHS-THEORY OF EQUATIONS-Exercise (Questions Asked In Previous 13 Years Exam)
- The smallest value of k, for which both the roots of the equation, x^2...
Text Solution
|
- If the roots of the equation b x^2+""c x""+""a""=""0 be imaginary, ...
Text Solution
|
- Q. Let p and q real number such that p!= 0,p^2!=q and p^2!=-q. if alph...
Text Solution
|
- Conder the function f(x)=1+2x+3x^2+4x^3 Let the sum of all distinct ...
Text Solution
|
- Let alpha and beta be the roots of x^2-6x-2=0 with alpha>beta if an=al...
Text Solution
|
- The value of b for which the equation x^2+bx-1=0 and x^2+x+b=0 have on...
Text Solution
|
- The number of distinct real roots of x^4 - 4 x^3 + 12 x^2 + x - 1 = 0...
Text Solution
|
- Let for a != a1 != 0 , f(x)=ax^2+bx+c ,g(x)=a1x^2+b1x+c1 and p(x) = f(...
Text Solution
|
- 8. Sachin and Rahul attempted to solve a quadratic equation. Sachin ma...
Text Solution
|
- let alpha(a) and beta(a) be the roots of the equation ((1+a)^(1/3)-1)x...
Text Solution
|
- Show that the equation e^(sinx)-e^(-sinx)-4=0 has no real solution.
Text Solution
|
- If the equation x^2+2x+3=0 and ax^2+bx+c=0 have a common root then a:...
Text Solution
|
- If a in R and the equation -3(x-[x])^2+""2""(x-[x])""+a^2=""0 (whe...
Text Solution
|
- Let alpha and beta be the roots of equation px^2 + qx + r = 0 , p != ...
Text Solution
|
- Let a in R and let f: R to R be given by f(x) =x^(5) -5x+a. then
Text Solution
|
- The quadratic equation p(x)=0 with real coefficients has purely imagin...
Text Solution
|
- Let S be the set of all non-zero numbers alphasuch that the quadratic ...
Text Solution
|
- The sum of all real values of X satisfying the equation (x^2-5x+5)^(x^...
Text Solution
|
- Let -1/6 < theta < -pi/12 Suppose alpha1 and beta1, are the root...
Text Solution
|
- If, for a positive integer n, the quadratic equation, x(x + 1) + (x + ...
Text Solution
|