Text Solution
Verified by Experts
Topper's Solved these Questions
SETS, RELATIONS AND FUNCTIONS
ARIHANT MATHS|Exercise Exercise For Session 1|11 VideosSETS, RELATIONS AND FUNCTIONS
ARIHANT MATHS|Exercise Exercise For Session 2|10 VideosSEQUENCES AND SERIES
ARIHANT MATHS|Exercise Exercise (Questions Asked In Previous 13 Years Exam)|38 VideosTHE STRAIGHT LINES
ARIHANT MATHS|Exercise Exercise (Questions Asked In Previous 13 Years Exam)|18 Videos
Similar Questions
Explore conceptually related problems
ARIHANT MATHS-SETS, RELATIONS AND FUNCTIONS -Exercise (Questions Asked In Previous 13 Years Exam)
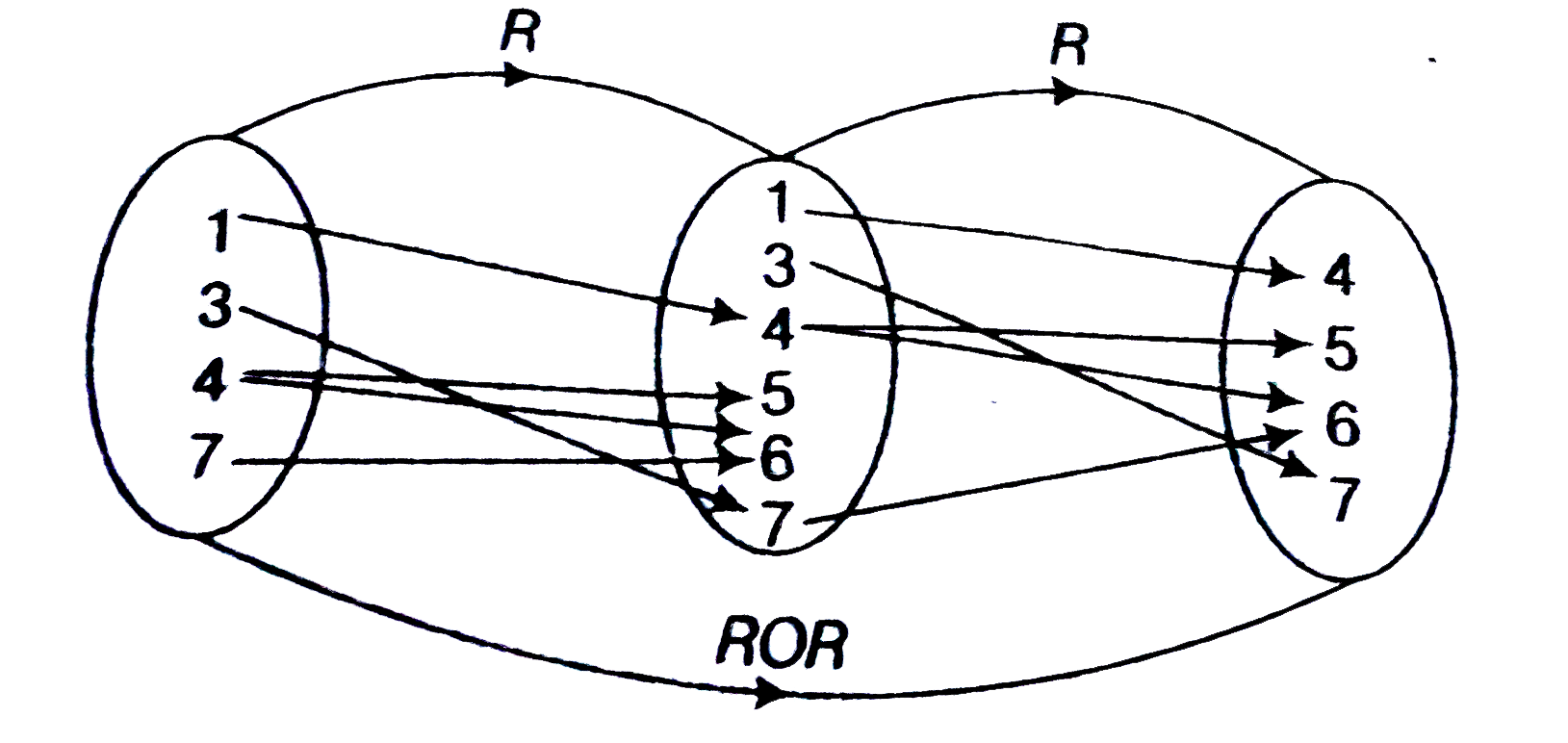
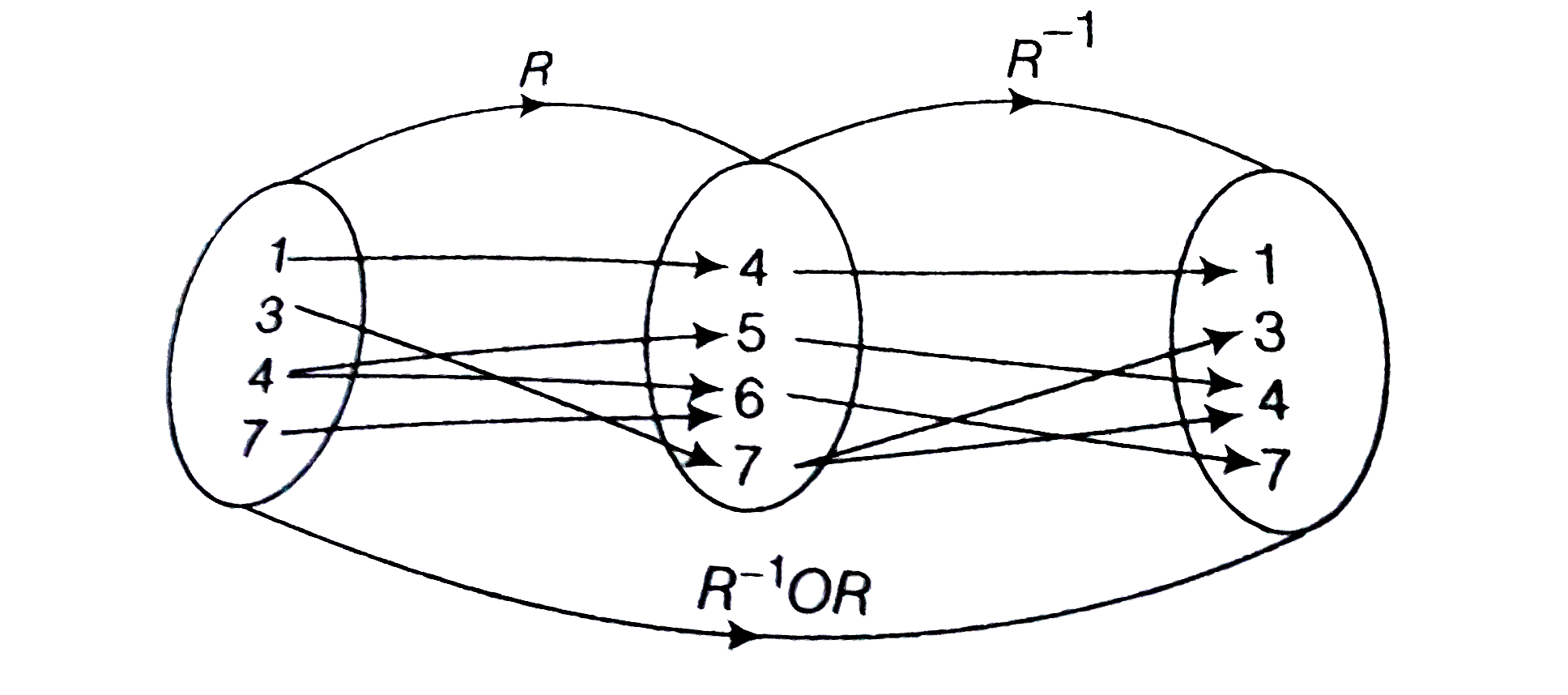
- Let R be a relation such that R = {(1,4), (3,7), (4,5), (4,6), (7,6)},...
Text Solution
|
- Let R = {(3, 3), (6, 6), (9, 9), (6, 12), (3, 9), (3, 12), (3, 6)} is ...
Text Solution
|
- Let w denote the words in the english dictionary. Define the relation ...
Text Solution
|
- Let R be the real line. Consider the following subsets of the plane...
Text Solution
|
- If A, B and C are three sets such that AnnB""=""AnnC and AuuB""=""AuuC...
Text Solution
|
- Let S={1,,2,34} . The total number of unordered pairs of disjoint s...
Text Solution
|
- Consider the following relations: R = {(x, y) | x, y are real numbers ...
Text Solution
|
- Let P={theta:sintheta-costheta=sqrt2cos theta}and Q={theta:sintheta+c...
Text Solution
|
- find the value of the
Text Solution
|
- Let R be the set of real numbers. Statement-1 : A""=""{(x ,""y) in R"...
Text Solution
|
- If A and B two sets containing 2 elements and 4 elements, respectively...
Text Solution
|
- If X""=""{4^n-3n-1"":""n in N}""a n d""Y""=""{9(n-1)"": n in N} , wh...
Text Solution
|
- Let A and B be too sets containing four and two elements respectively ...
Text Solution
|