Home
Class 12
MATHS
If vec a , vec b are any two vectors, t...

If ` vec a , vec b` are any two vectors, then give the geometrical interpretation of g relation `| vec a+ vec b|=| vec a- vec b|`

Text Solution

Verified by Experts

Let OA=a and AB=b. completing the parallelogram OABC.

Then, OC=b and CB=a
from `DeltaOAB`, we have
`OA+AB=Obimpliesa+b=OB` . . . (i)
From `DeltaOCA,` we have
`OC+CA=OA`
`impliesb+CA=aimpliesCA=a-b` . . . (ii)
Clearly, `|a+b|=|a-b|implies |OB|=|CA|`
Diagonals of parallelogram OABC are qual.
OABC is a rectangle.
`implies OA bot OC implies a bot b`.
Promotional Banner

Topper's Solved these Questions

  • VECTOR ALGEBRA

    ARIHANT MATHS|Exercise Exercise For Session 1|7 Videos

  • VECTOR ALGEBRA

    ARIHANT MATHS|Exercise Exercise For Session 2|17 Videos

  • TRIGONOMETRIC FUNCTIONS AND IDENTITIES

    ARIHANT MATHS|Exercise Exercise (Questions Asked In Previous 13 Years Exam)|19 Videos

Similar Questions

Explore conceptually related problems

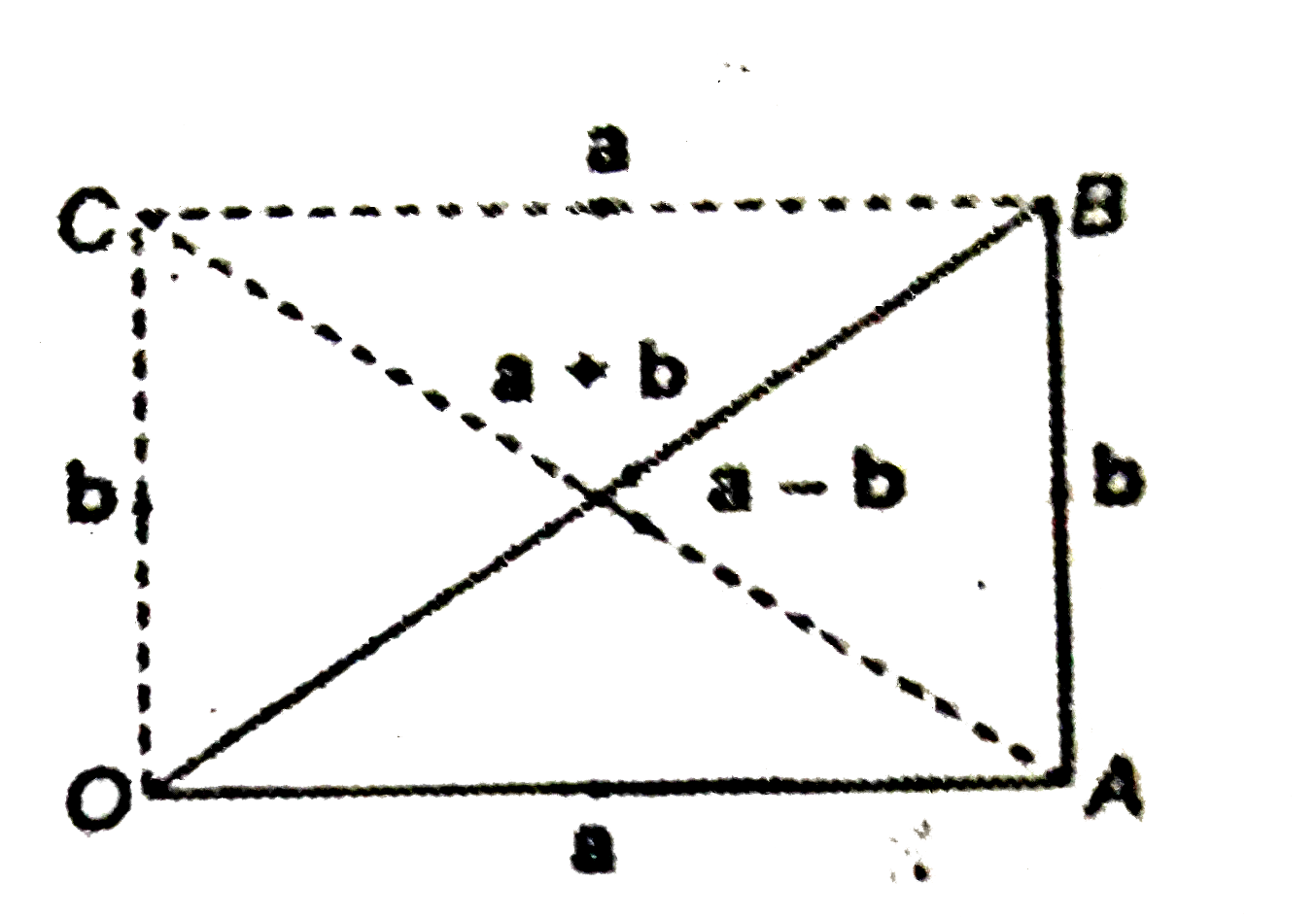
If vec a,vec b are any two vectors,then give the geometrical interpretation of g relation |vec a+vec b|=|vec a-vec b|

If vec a , vec b are two vectors, then write the truth value of the following statements: vec a=- vec b| vec a|=| vec b| | vec a|=| vec b| vec a=+- vec b | vec a|=| vec b| vec a= vec b

Show that (vec a-vec b)xx(vec a+vec b)=2vec a xxvec b and given a geometrical interpretation of it.

If vec a and vec b are two vectors such that (vec a+vec b)vec a-vec b=0 find the relation between the magnitudes of vec a and vec b

vec a, vec b, vec c, dare any four vectors then (vec a xxvec b) xx (vec c xxvec d) is a vector Perpendicular to vec a, vec b, vec c, vec d

For any two vectors vec a, vec b | vec a * vec b | <= | vec a || vec b |

For any two vectors vec a and vec b prove that | vec a + vec b | <= | vec a | + | vec b |

If vec a and vec b are two vectors such that |vec a+vec b|=|vec a|, then prove that vector 2vec a+vec b is perpendicular to vector vec b

For any vector vec a and vec b prove that |vec a+vec b|<=|vec a|+|vec b|

If vec a and vec b are orthogonal unit vectors, then for a vector vec r noncoplanar with vec a and vec b , vector rxxa is equal to a. [ vec r vec a vec b] vec b-( vec r. vec b)( vec bxx vec a) b. [ vec r vec a vec b]( vec a+ vec b) c. [ vec r vec a vec b] vec a-( vec r. vec a) vec axx vec b d. none of these