Text Solution
Verified by Experts
Topper's Solved these Questions
Similar Questions
Explore conceptually related problems
CENGAGE CHEMISTRY-IONIC EQUILIBRIUM-Archives Subjective
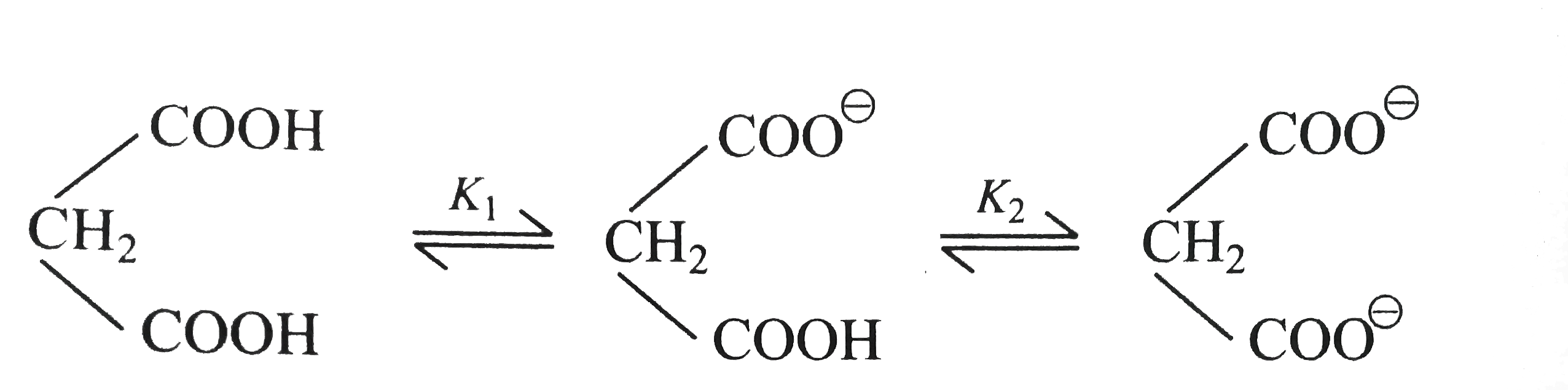
- Malonic acid is an organic dibasic acid such as H(2)S having first ion...
Text Solution
|
- How much moles of sodium propionate should be added to 1L of an aqueou...
Text Solution
|
- Given reason for the statement that the pH of an aqueous solution of s...
Text Solution
|
- 20 mL of 0.2M sodium hydroxide is added to 50 mL of 0.2 M acetic acid ...
Text Solution
|
- The dissociation constant of a weak acid HA si 4.9 xx 10^(-8). After m...
Text Solution
|
- A solution contains a mixture of Ag^(+)(0.10M) and Hg(2)^(2+)(0.10M) w...
Text Solution
|
- The concentration of hydrogen ions in a 0.2M solution of formic acid i...
Text Solution
|
- The solubility of Mg (OH)(2) in pure water is 9.57 xx 10^(-3) gL^(-1)....
Text Solution
|
- What is the pH of the solution when 0.20 mol of HCI is added to 1L of ...
Text Solution
|
- How many gram moles of HCI will be required to prepare 1L of buffer so...
Text Solution
|
- Freshly precipiteated Al and Mg hydroxides are stirred vigorously in a...
Text Solution
|
- What is the pH of 1 M solution of acetic acid ? To what volume one lit...
Text Solution
|
- A 50 mL solution of weak base BOH is titrated with 0.1N HCI solution. ...
Text Solution
|
- The K(SP) of Ag(2)C(2)O(4) at 25^(@)C is 1.29xx10^(-11)mol^(3)L^(-3). ...
Text Solution
|
- The K(SP)of Ca(OH)(2)is 4.42xx10^(-5)at 25^(@)C. A 500 mL of saturated...
Text Solution
|
- The pH of blood stream is maintained by a proper balance of H(2)CO(3) ...
Text Solution
|
- An aqueous solution of a metal bromide MBr(2)(0.05M) is saturated with...
Text Solution
|
- For the reaction Ag(CN)(2)^(ɵ)hArr Ag^(o+)+2CN^(ɵ), the K(c ) at 25^...
Text Solution
|
- Calculate the pH of an aqueous solution of 1.0M ammonium formate assum...
Text Solution
|
- What is the pH of a 0.50M aqueous NaCN solution ? (pK(b)of CN^(-)=4.70...
Text Solution
|
- The ionization constant of overset(o+)(NH(4)) ion in water is 5.6 xx 1...
Text Solution
|