Home
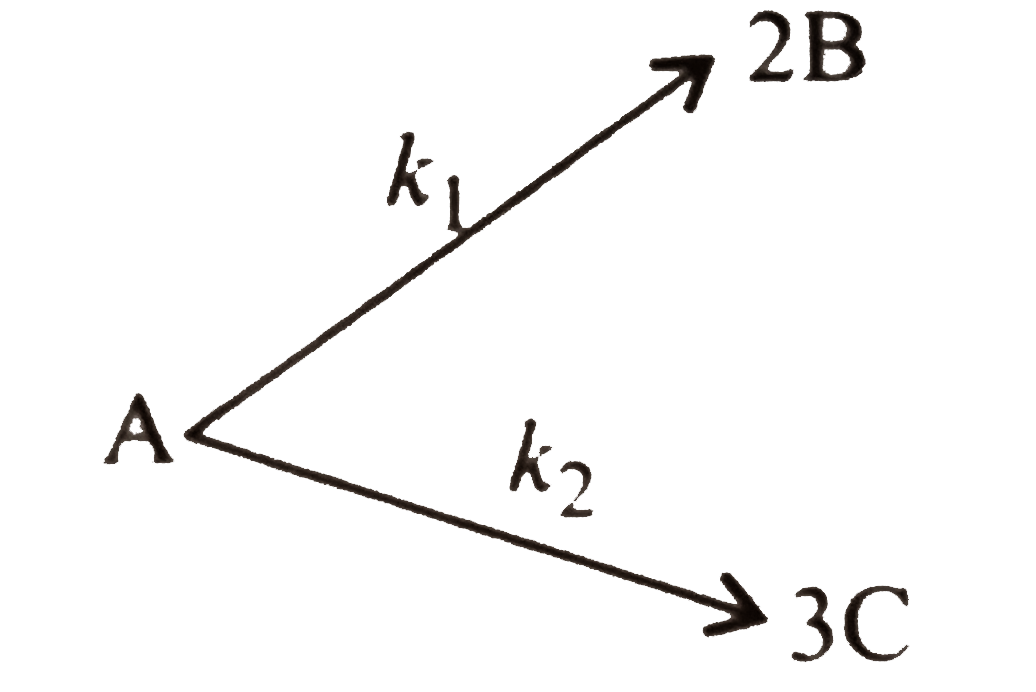
Class 12
CHEMISTRY
Consider the following parallel reaction...

Consider the following parallel reactions being given by `A(t_(1//2) = 1.386 xx 10^(2) hours)`, each path being first order.

If the distribution of `B` in the Product mixture is `50%`, the partical half life of `A` for converison into `B` is

A

`A. 346.5 h`

B

`B. 131 h`

C

`C. 115.5 h`

D

`D. 31 h`

Text Solution

Verified by Experts

The correct Answer is:
A
`(2k_(1))/(2k_(1) + 3k_(2)) = 0.5` and
`k_(1) + k_(2) = (0.693)/(1.386 xx 10^(2)) =5 xx 10^(-3)h^(-1)`
Solving `(k_(1))/(k_(2)) = (2)/(3)` and `k_(1) = 2 xx 10^(-3) h^(-1)` and
`k_(2) = 3 xx 10^(-3) h^(-1)`
`t_(1//2(A rarr B)) = (0.693)/(k_(2)) = (0.693)/(3 xx 10^(-3)) = 231 h`
Promotional Banner

Topper's Solved these Questions

  • CHEMICAL KINETICS

    CENGAGE CHEMISTRY|Exercise Ex 4.3 More Than One Correct|5 Videos

  • CHEMICAL KINETICS

    CENGAGE CHEMISTRY|Exercise Ex4.4 Objective|10 Videos

  • CHEMICAL KINETICS

    CENGAGE CHEMISTRY|Exercise Ex 4.2 (Objective)|10 Videos

  • CARBOXYLIC ACIDS AND THEIR DERIVATIVES

    CENGAGE CHEMISTRY|Exercise Exercises Archives (Analytical And Descriptive)|34 Videos

  • COORDINATION COMPOUNDS

    CENGAGE CHEMISTRY|Exercise Archives Subjective|18 Videos

Similar Questions

Explore conceptually related problems

Consider the following parallel first order reactions: Half-life of the overall decay of A is 2 ys while half-life for the formation of B is 3yr. Half-life for the formation for C (in years) is :

A first order gas reaction has k = 1.5 xx 10^(-6) s^(-1) at 200^(@)C . If the reaction is allowed to run for 10 h , what have changed in the Product? What is the half-life of this reaction?

Half life ( t_1 ) of the first order reaction and half life ( t_2 ) of the 2 ""^(nd) order reaction are equal. If initial concentration of reactants in both reaction are same then ratio of the initial rate of the reaction

For the following elementary first order reaction: If k_(2)=2k_(1) , then % of B in overall product is:

When temperature of a reaction mixture is changed from T_(1) to T_(2) half life is found to decrease thus,

Half-life (t_(1)) of the first order reaction and half-life (t_(2)) of the second order reaction are equal. Hence ratio of the rate at the start of the start of the reaction: