गुटके A पर लगनेवाले बल हैं,
(i) धरती द्वारा `m_(A)g`, निचे की ओर ,
(ii) डोरी द्वारा T, ऊपरे की ओर |
परिणामी बल निचे की ओर `=m_(A)g-T`.
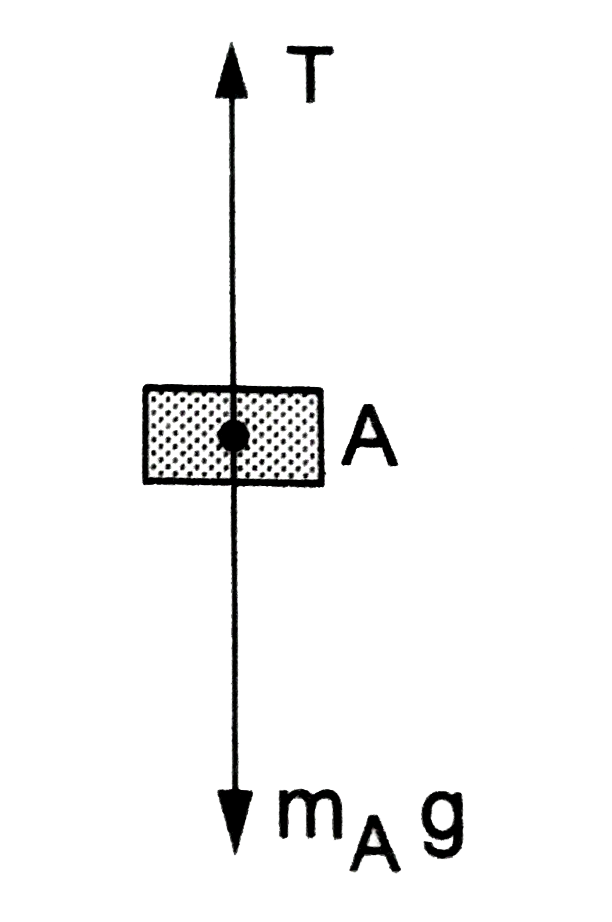
यदि A का त्वरण निचे की ओर a हो, तो F = ma से,
`m_(A)g-T=m_(A)a." "...(i)`
हमें a का मान निकालना है | इस समीकरण में हमें T का मान पता नहीं है | अत :, यहाँ से सीधे a का मान नहीं लिख सकते | हमें कम-से-कम एक और समीकरण चाहिए जो गुटके B का विचार करने से मिल सकता है |
गुटके B पर लगनेवाले बल हैं,
(i) धरती द्वारा `m_(B)g`, निचे की ओर,
(ii) डोरी द्वारा T, ऊपर की ओर |

चूँकि डोरी तथा घिरनी के भार नगण्य हैं और वे घर्षणरहित हैं, इसलिए डोरी के दोनों हिस्सों में तनाव बराबर होगा | अत :, जो T पिछले समीकरण में लिखा गया था वही T यहाँ भी लिखा जा रहा है | चूँकि A का त्वरण a निचे की ओर लिया गया था, इसलिए B का त्वरण ऊपर की ओर a होगा | F = ma समीकरण से,
`T-m_(B)g=m_(B)a." "...(ii)`
समीकरण (i) तथा (ii) को जोड़ने पर,
`m_(A)g-m_(B)g=m_(A)a+m_(A)a`
या `" "a=((m_(A)-m_(B))/(m_(A)+m_(B)))g.`

