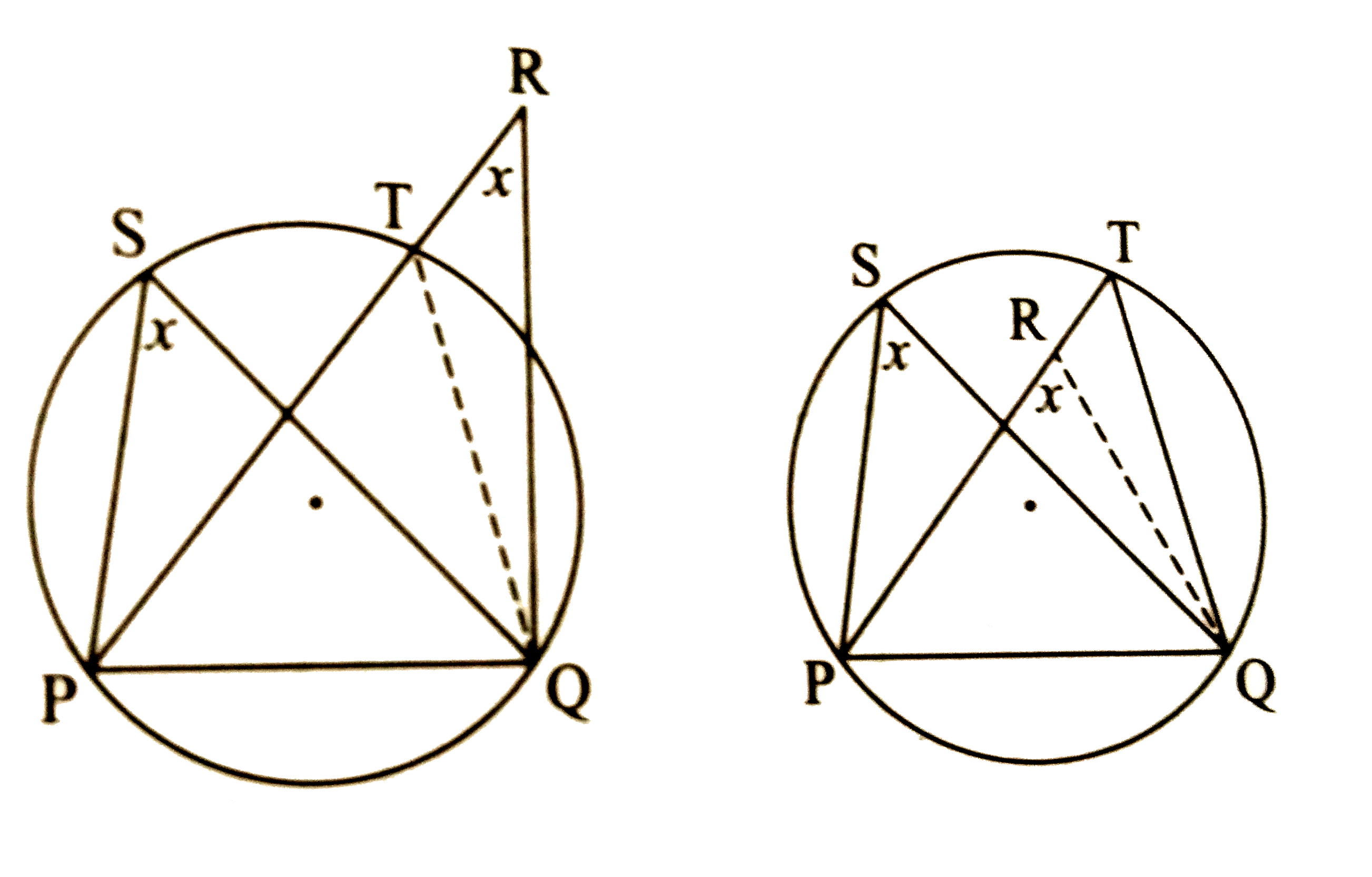Text Solution
Verified by Experts
Topper's Solved these Questions
Similar Questions
Explore conceptually related problems
NAVNEET PUBLICATION - MAHARASHTRA BOARD-THEOREMS -CIRCLE
- Theorem:A line drawn through the end point of a radius and perpendicul...
Text Solution
|
- Theorem: The length of two tangents drawn from an external point to a ...
Text Solution
|
- If two circles touch each other (internally or externally); the point ...
Text Solution
|
- If two arcs of a circle (or of congruent circles) are congruent, then ...
Text Solution
|
- If two chords of a congruent circle are equal; then their correspondin...
Text Solution
|
- Inscribed Angle Theorem The measure of an inscribed angle is half ...
Text Solution
|
- Corollaries of inscribed angle theorem : Angle inscribed in the sa...
Text Solution
|
- In the figure, O is the centre of the circle. Seg AC is the diameter /...
Text Solution
|
- The sum of either pair of opposite angles of a cyclic quadrilateral is...
Text Solution
|
- Given : square ABCD is cyclic. /DCE is an exterior angle of ...
Text Solution
|
- If a line segment joining two points subtends equal angles at two othe...
Text Solution
|
- Theorem of angle between tangent and secant If an angle has its ve...
Text Solution
|
- Theorem of internal division of chords. Suppose two chords of a cir...
Text Solution
|
- Theorem of external division of chords. If secants containing chords...
Text Solution
|
- Tangent Secant Theorem Point E is in the exterior of a circle. A sec...
Text Solution
|