Text Solution
Verified by Experts
Topper's Solved these Questions
PYTHAGORAS THEOREM
NAVNEET PUBLICATION - MAHARASHTRA BOARD|Exercise 3.5 (4 mark each)|4 VideosPYTHAGORAS THEOREM
NAVNEET PUBLICATION - MAHARASHTRA BOARD|Exercise Assignment 3.1|8 VideosPYTHAGORAS THEOREM
NAVNEET PUBLICATION - MAHARASHTRA BOARD|Exercise 3.3 (2 mark each)|8 VideosPROBABILITY
NAVNEET PUBLICATION - MAHARASHTRA BOARD|Exercise ASSIGNEMENT 5.4|12 VideosQUADRATIC EQUATION
NAVNEET PUBLICATION - MAHARASHTRA BOARD|Exercise CHALLENGIN QUESTIONS|2 Videos
Similar Questions
Explore conceptually related problems
NAVNEET PUBLICATION - MAHARASHTRA BOARD-PYTHAGORAS THEOREM-3.4 (3 mark each)
- square ABCD is a parallelogram. The diagonals AC and BD intersect at p...
Text Solution
|
- Find the side and perimeter of a square whose diagonal is 10cm.
Text Solution
|
- In the figure, /DFE=90^(@), seg FG bot side DE, DG=8, FG=12 then compl...
Text Solution
|
- In the figure, M is the midpoint of QR. /PRQ=90^(@). Prove that PQ^(2)...
Text Solution
|
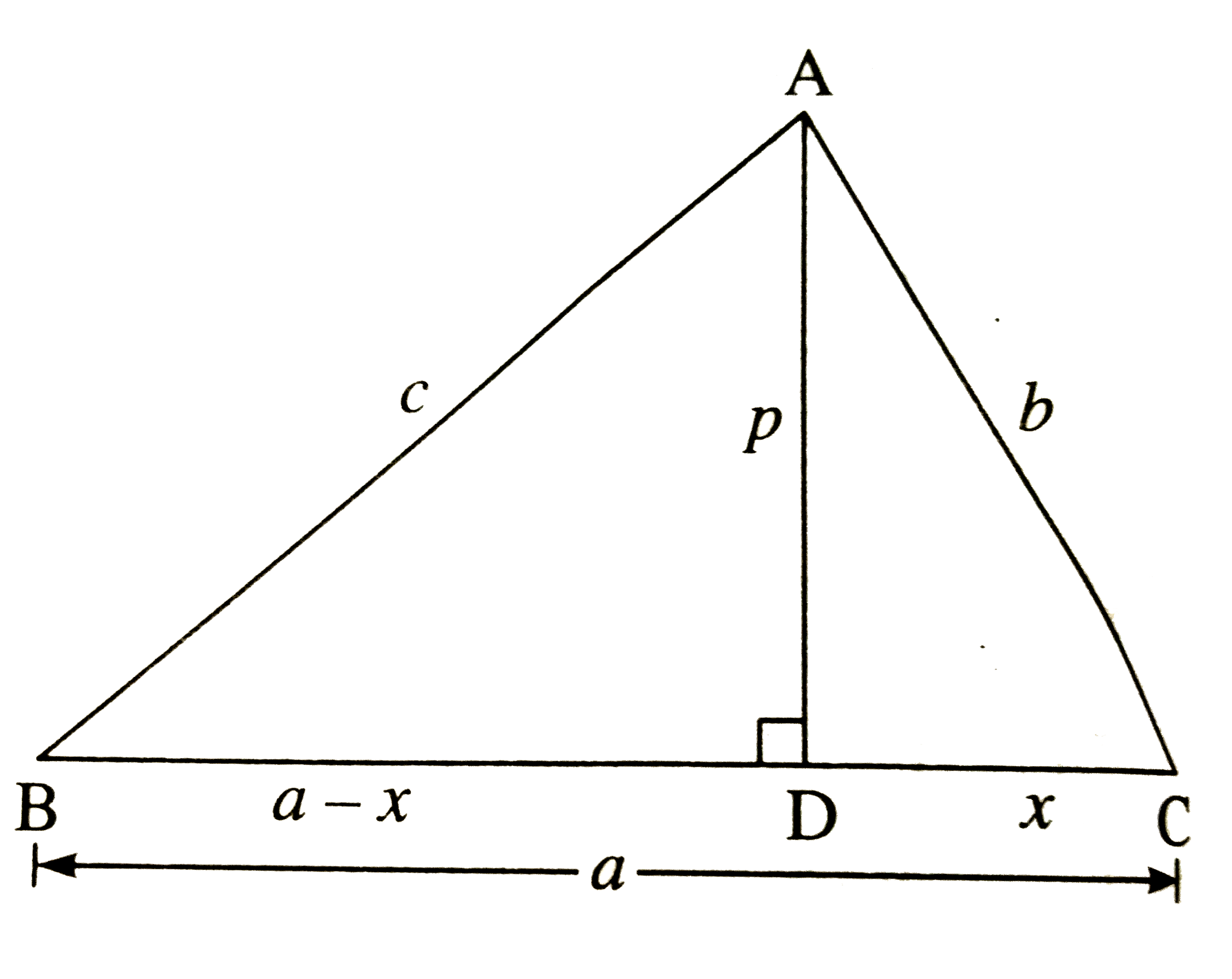
- In DeltaABC, /C is an acute angle, seg AD bot seg BC. Prove AB^(2)=BC^...
Text Solution
|
- In DeltaPQR, seg PM is median. PM=9, PQ^(2)+PR^(2)=290 then find lengt...
Text Solution
|
- The perpendicular sides of a right angled triangle are 3x and 4x. The ...
Text Solution
|
- In the figure, AD=17, AB=10, BC=15. /ABC=/BCD=90^(@) seg AE bot side C...
Text Solution
|
- In DeltaRST, /S=90^(@). /T=30^(@), RT=12cm, then find RS and ST.
Text Solution
|